黄乐天

浅谈模拟退火算法

背景

在实际生活中， 数学问题中，我们常常会遇到(一定范围内)函数求最值的问题。一般可以用数学方式解答，但如果遇到如下恶心的函数：

它的函数图像是这样的：

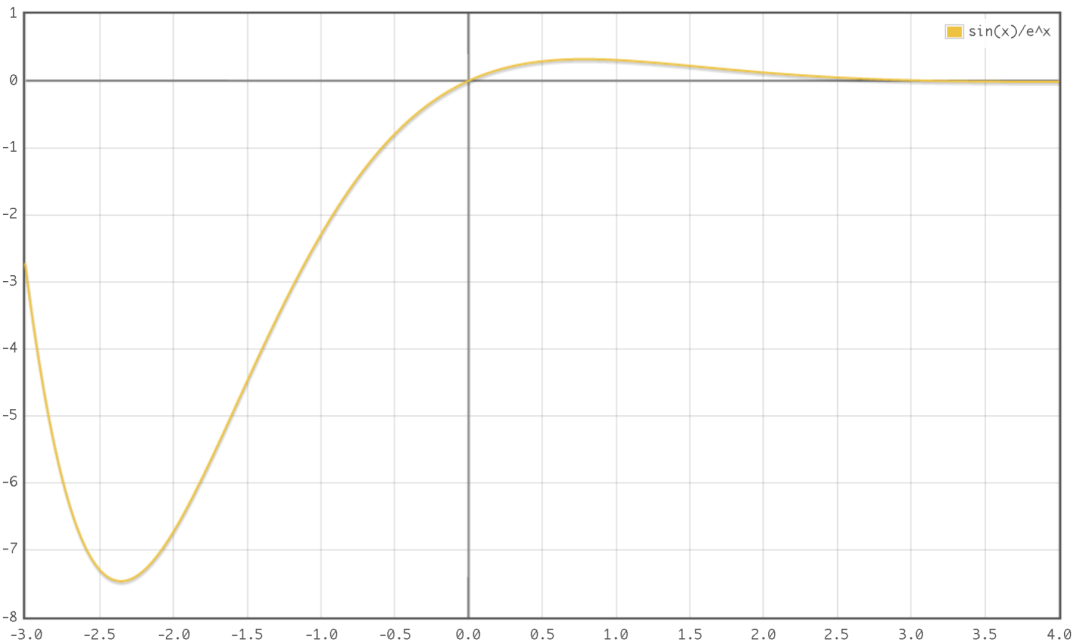
我们只好用计算机科学 (说白了就是编程) 来计算了。

对于这种单峰函数，可以使用“爬山算法”来得出结果，即每次在当前最优解附近找一个解，若比当前最优解更优则接受它。

但它的缺点十分明显，就是容易陷入局部最优解，如果遇到下面的

多峰函数：

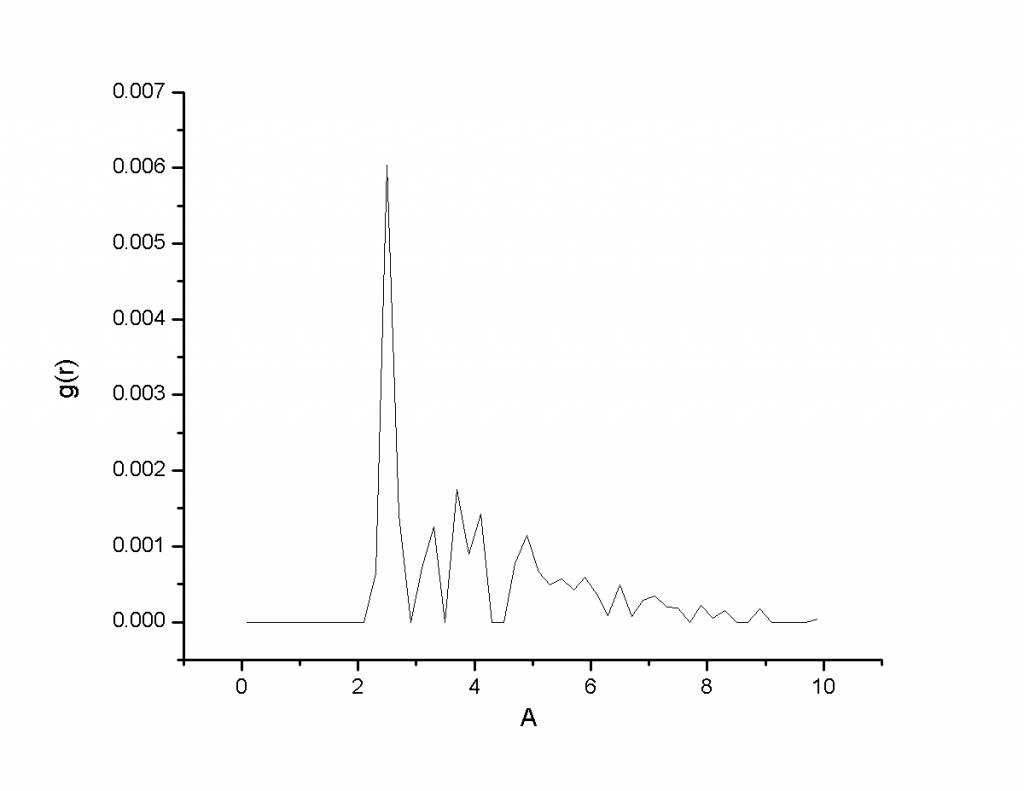
(我也不知道这g(r)是咋来的)

我们可以使用一种玄学算法——模拟退火

模拟退火是啥？

模拟退火算法(Simulated Annealing，SA)最早的思想是由N. Metropolis等人于1953年提出。1983 年,S. Kirkpatrick 等成功地将退火思想引入到组合优化领域。它是基于Monte-Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法从某一较高初温出发，伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法，理论上算法具有概率的全局优化性能,目前已在工程中得到了广泛应用，诸如VLSI、生产调度、控制工程、机器学习、神经网络、信号处理等领域。

——百度百科

实际上，SA广泛运用于信息学竞赛(Olympiad in Informatics，OI)，在OIers(即信竞生)想不出某道数据范围较小的题的正解时用来骗分。

看看它的原理：

模拟退火算法来源于固体退火原理，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。根据Metropolis准则，粒子在温度T时趋于平衡的概率为e(-ΔE/(kT))，其中E为温度T时的内能，ΔE为其改变量，k为Boltzmann常数。用固体退火模拟组合优化问题，将内能E模拟为目标函数值f，温度T演化成控制参数t，即得到解组合优化问题的模拟退火算法：由初始解i和控制参数初值t开始，对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代，并逐步衰减t值，算法终止时的当前解即为所得近似最优解，这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制，包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。

——百度百科

物理?...感觉这段话只有小唐能看懂

用人话来说，这是一种求多峰函数最值的算法。原理是模拟固体降温的过程，并在此过程中产生新解。随着温度的降低，产生新解的变化越来越小，越来越集中在最优解附近。直到温度低至一定的最低温，即“结晶”，则停止此过程，当前的最优解基本上就是全局最优解了。

还不理解？上图！

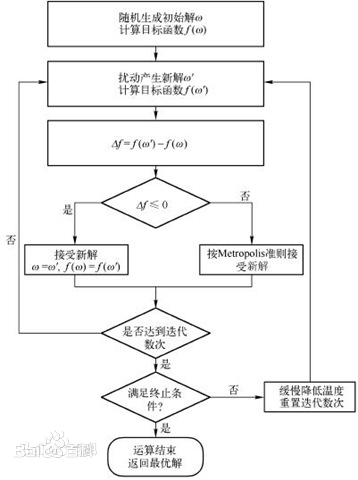
过程也应该很好理解，直接上动图吧

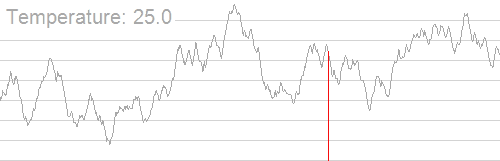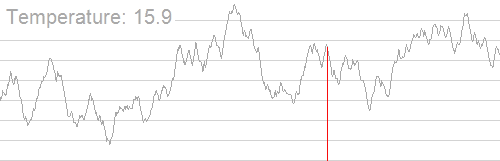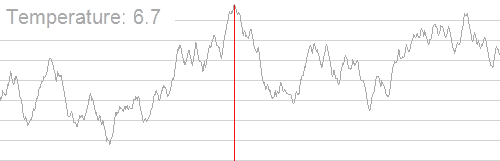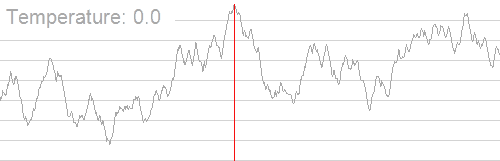
我们用几个变量来理性理解此过程(以求多峰函数最小值为例)

:常量，模拟退火的初始温度，一般设在

模拟退火的当前温度

常量，模拟退火的目标温度，一般设为

常量，模拟退火的温度变动量，一般比小一点点，乘上得到下一个温度

当前得到的最优解结果(当前求到的函数最小值)

新得到的解

上一个被接受的解

解的变化量，即的结果

那么模拟退火的具体过程就是，由初温开始，每次乘以得到当前温度，若$t

在这个过程中，我们在上一被接受的解的基础上随机浮动产生新解。但是注意，每次的浮动大小与当前温度有关，若小则浮动相对也更小。我们通过一系列随机数的操作再乘来得出浮动大小，最后加上得出新解。

接着我们计算由所得的结果(求函数值)，减去得到解的变动量。若，则我们遇到了一个更小的结果，即更优的解，那么当然要接受它——更新变为新解的结果，变为。如果，则这是个更劣的解，我们当然不要更新，那是否接受这个解(更新)呢？我们使用Metropolis接受准则，对于接受这个解，它的概率是，再判断这个概率是否大于一个大于、小于等于的随机数来接受即可。

对于这个概率的理解，我们引用一位神犇的思想：对于，如果它较大，就说明我们遇到了一个非常劣的解，则接受它的概率极小，因为很小；反之接受的概率较大，因为相对较大。对于，随时间增加而减小，所以用来除以。而且，对于整个式子，较大的时候我们会接受大部分解，较小时只会接受较小的解。

例题/C++代码实现

如果看不懂代码，可以在菜鸟教程学习基础语法就绝对能看懂了，当然我自己也会加上详细注释。

例题：UVA10228 A Star not a Tree?

原题面是英文的，我写一下中文题面吧...

题目描述

给定一个边形所有顶点坐标，求其费马点到所有顶点距离和

费马点是指到多边形所有顶点距离和最小的点

输入格式

第一行一个正整数，其后行，每行两个整数。

输出格式

一行，即费马点到所有顶点距离和，精确到整数。

题目分析

我们可以通过模拟退火来找出其费马点，只用改变每个解(坐标)对结果的计算即可。

原来我们举的例子是计算函数，把解直接代入即可。而在这题中，计算结果的方式变为计算此坐标到每个顶点的距离之和。计算距离的方式应该不用我多说，就是利用勾股定理求欧几里得距离，则到的距离为。

核心代码如下：

//头文件等不展示了
//...和/*...*/均为注释
//定义变量
int n;//int为整型变量，储存一个[-2^32,2^31-1]的整数，这里表示定义一个整型变量n，即多边形边的数量
double ans=1e18;//double是“双精度浮点数”，即较为精确的小数，储存范围很大
//这里把ans的初始值定为10^18，因为取最小值，后面直接比较就好
double px[105],py[105];//double类型数组，一个数组(如px)可储存105个double类型的数，因为n最大为100
//如需访问第i个点的x轴上的值，为px[i]
const double eps=1e-15;//定义常量eps，const为常量关键字
double calc(double x,double y)//计算此坐标到所有顶点的距离和{//这是一个“double”的函数，返回值则也为double类型
    double res=0;//储存结果的变量
    for(int i=1;i<=n;i++)//i从1到n循环
        s+=sqrt((x-px[i])*(x-px[i])+(y-py[i])*(y-py[i]));//计算距离，sqrt是开方函数
    return res;//返回结果
}
void SA()//模拟退火的核心{//这是个"void"的函数，没有像calc一样的返回值return res
    //rand()是随机函数，一个区间[0,32767]的整数
    //=是赋值操作，a=b表示把b赋值给a
    double x=rand()%10000,y=rand()%10000;//最初始的解随机得出
    //%是取余
    double t=3000;//模拟退火的温度
    while(t>eps)//温度大于末温就一直循环
    {//while(condition){...}表示只要满足condition就执行"..."
        //RAND_MAX是rand()能达到的最大值，即32767
        double xx=x+(rand()*2-RAND_MAX)*t,yy=y+(rand()*2-RAND_MAX)*t;//随机操作再乘t
        //↑计算新解e
        double now=calc(xx,yy);//计算结果
        double dt=now-ans;//计算e_k
        if(dt<0)x=xx,y=yy,ans=now;//找到更优的解，则接受它
        else if(exp(-dt/t)>rand()/(RAND_MAX*1.0)/*rand()/RAND_MAX一定>0且<=1*/)//Metropolis准则
            x=xx,y=yy;//接受这个解，但不要更新ans，因为它不是最优解
        t*=0.996;//t乘上Δ
    }//+=,*=都也是赋值操作，如a+=b表示把a+b赋值给a
}
//输入和输出变量都在下面的主函数main()里，每个C/C++程序都要有一个main函数，所有操作都在里面
//包括上面的SA()也会在main()被调用
//int main(){...}
//这里只展示核心代码(模拟退火部分)，主函数就不写在这里了
//完整代码可以找我要

后记

写这篇文章只是为了让你们了解模拟退火的原理及过程，真正在实际生活应用可能还得等到大学或者工作的研究。当然，在别人问你求函数峰值的数学问题时，也可以拿出电脑跑一遍模拟退火来炫技[斜眼笑]...

如果有任何不理解的地方可以来问我，挂几个联系方式：

QQ:3038564494

邮箱:adayhlt526@gmail.com

参考资料

• 浅谈玄学算法——模拟退火 by M_sea(https://www.luogu.com.cn/blog/m-sea/qian-tan-SA)

• 模拟退火-维基百科(https://zh.wikipedia.org/wiki/模拟退火) (如果wiki上不去可以找我要图片)

• 模拟退火算法-百度百科(https://baike.baidu.com/item/模拟退火算法)

(1)2025——Music！嗨起来！

(2)几道你第一眼肯定做错的题

(3)那些英语“白大象”

(4)世界之大，远不及他心中碧海苍梧

扫码关注更多精彩

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！