机器学习入门实验之逻辑回归--批梯度下降法

机器学习入门实验之逻辑回归--批梯度下降法

• 机器学习入门课程复习：逻辑回归
• • 基于交叉熵代价函数的逻辑回归模型以及实现
  • • 机器学习入门实验之逻辑回归、python、numpy
  • 1. 获取数据
  • 2. 对数据进行标准化、归一化处理
  • 划分训练集和测试集
  • 实现算法
  • 测试效果及模型评估
  • 实验效果
• -*- coding:utf-8 -*-

机器学习入门课程复习：逻辑回归

基于交叉熵代价函数的逻辑回归模型以及实现

机器学习入门实验之逻辑回归、python、numpy

下面记录的是我做实验的过程以及为考试复习学过的内容，参考教材是《机器学习》微课版，作者陈喆，下面记录的是2.2节逻辑回归实验的内容，我的实验步骤如下：

1.获取数据
2.对数据进行标准化、归一化处理
3.划分训练集和测试集
4.实现算法
5.测试效果
6.全部代码

1. 获取数据

数据为alcohol_dataet.csv数据集，共384行6列数据，来自于课本附赠的实验资料，扫描课本二维码即可获取。

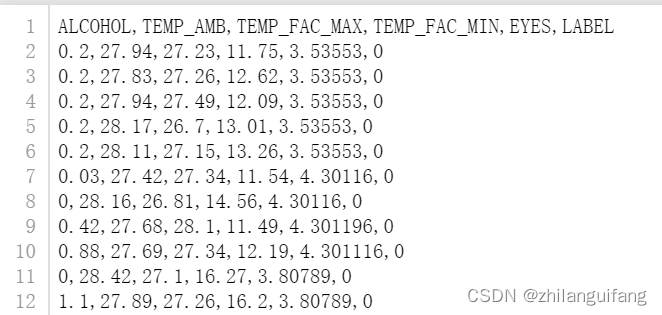
2. 对数据进行标准化、归一化处理

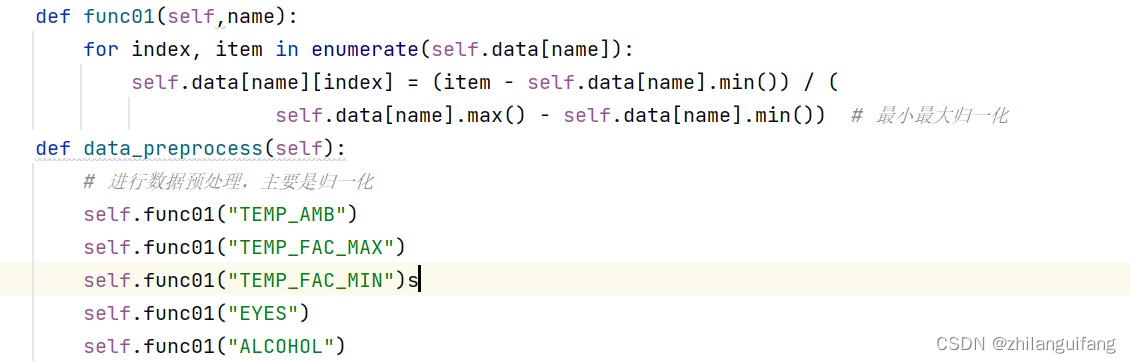
这里只是使用了归一化方法，归一化有最小最大归一化、均值归一化等方法，实验中用的是最小最大归一化，能够将数据缩放到0-1之间，从而消除数值较大的数据所造成的偏差（我是这么理解的），就是无量纲化处理。
归一化代码如下：

划分训练集和测试集

将数据前200条作为训练数据，剩下的作为测试数据，同时数据前5列作为特征，最后哦一列作为目标值。同时由于这里使用的是批梯度迭代算法，每次迭代前要打乱数据集的顺序。代码如下：

实现算法

实验采用批梯度下降算法，以交叉熵作为代价函数。由参数控制迭代次数，代码如下：

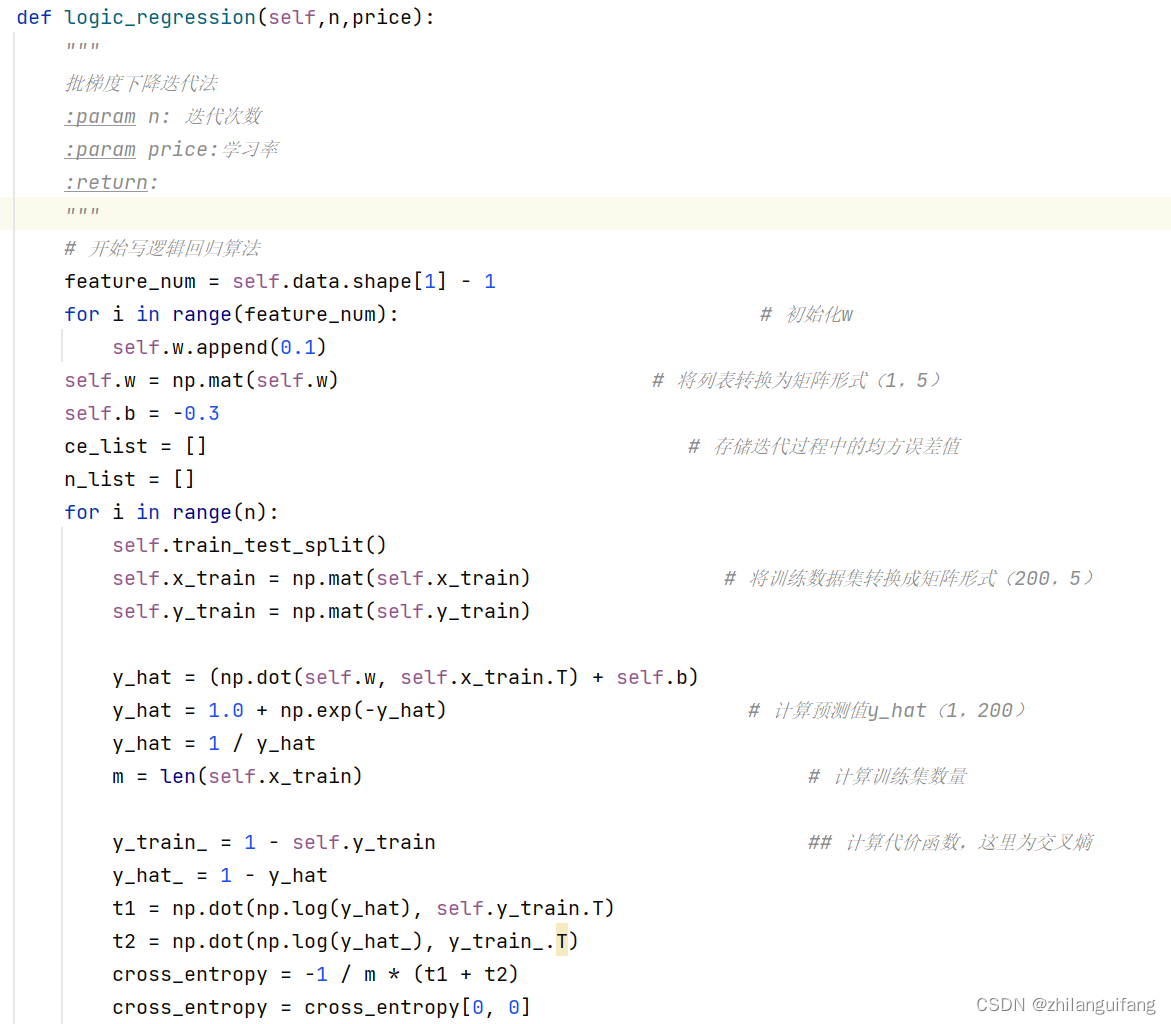
测试效果及模型评估

评估模型用的是召回率、精确率和f1值，代码如下：

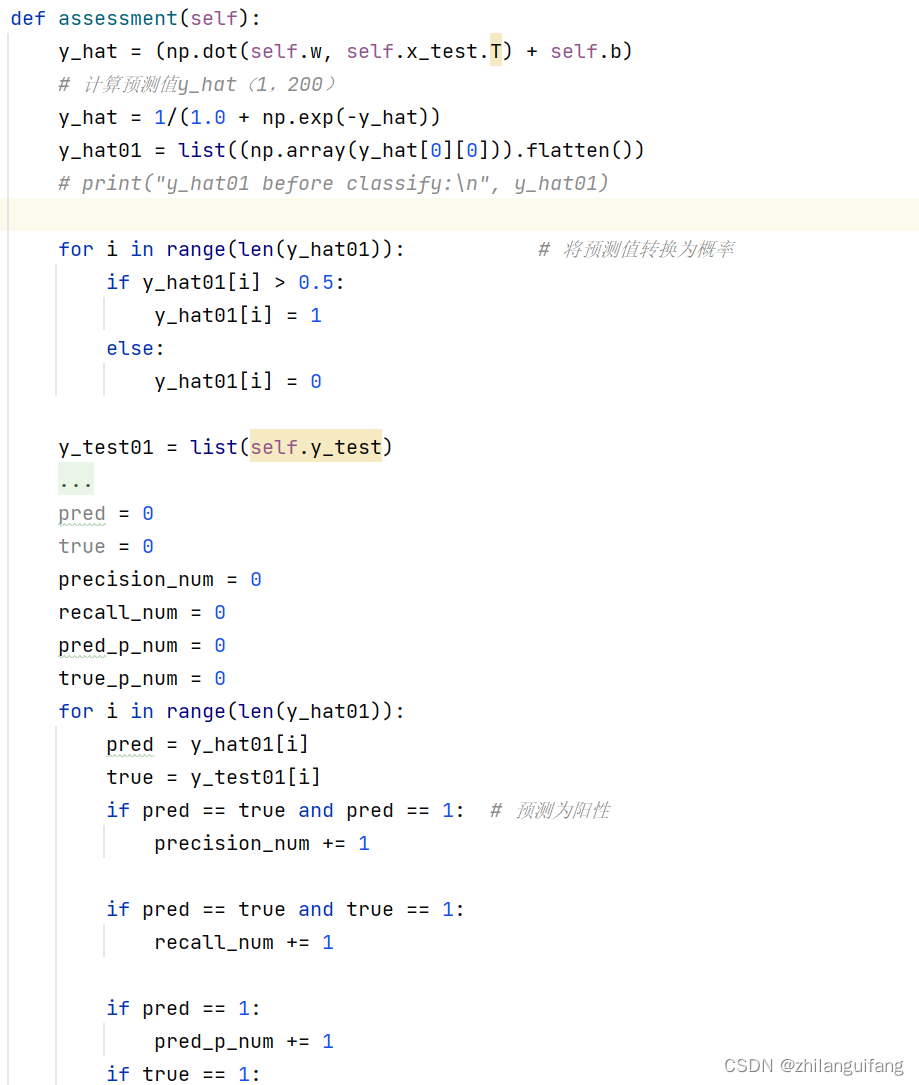
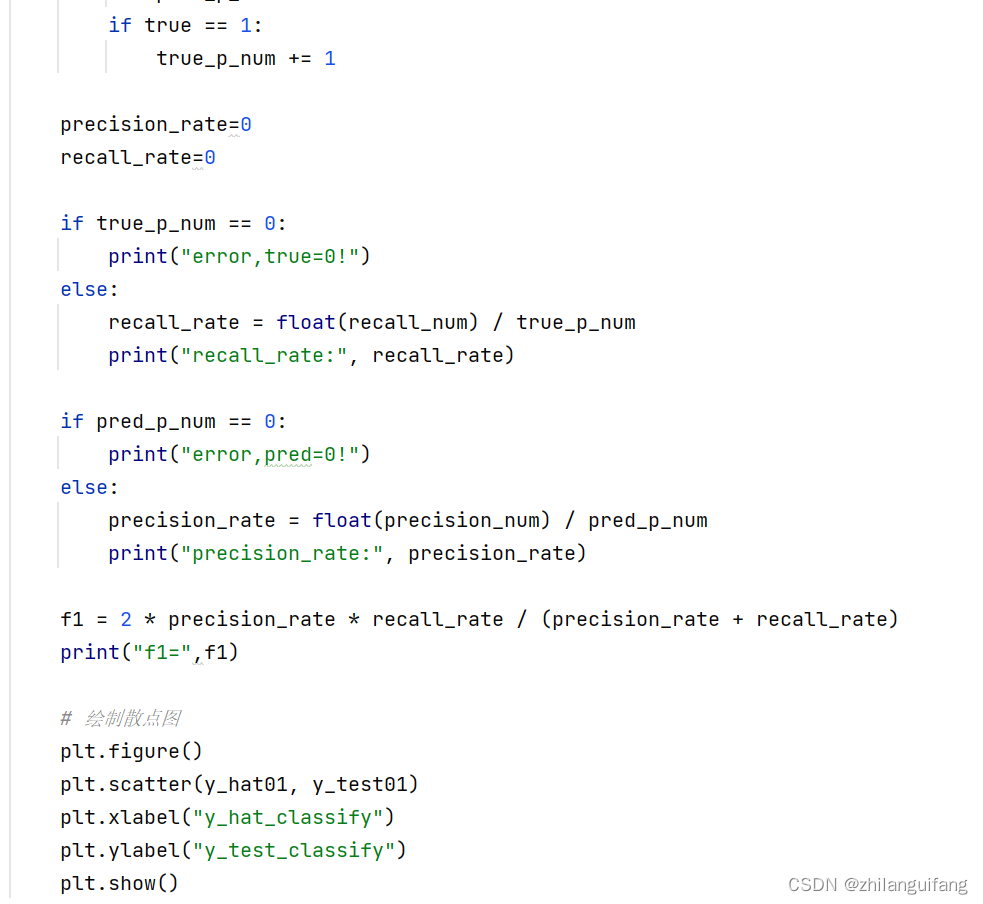
实验效果

最后，来看看模型预测效果如何吧

在这里，迭代了500次，每次步长为0.00025，w的所有分量初始值都设置为0.1，b的初始值设置为-0.3。经过多次调试，对于本次实验，这么设置参数得到的效果是最好的。

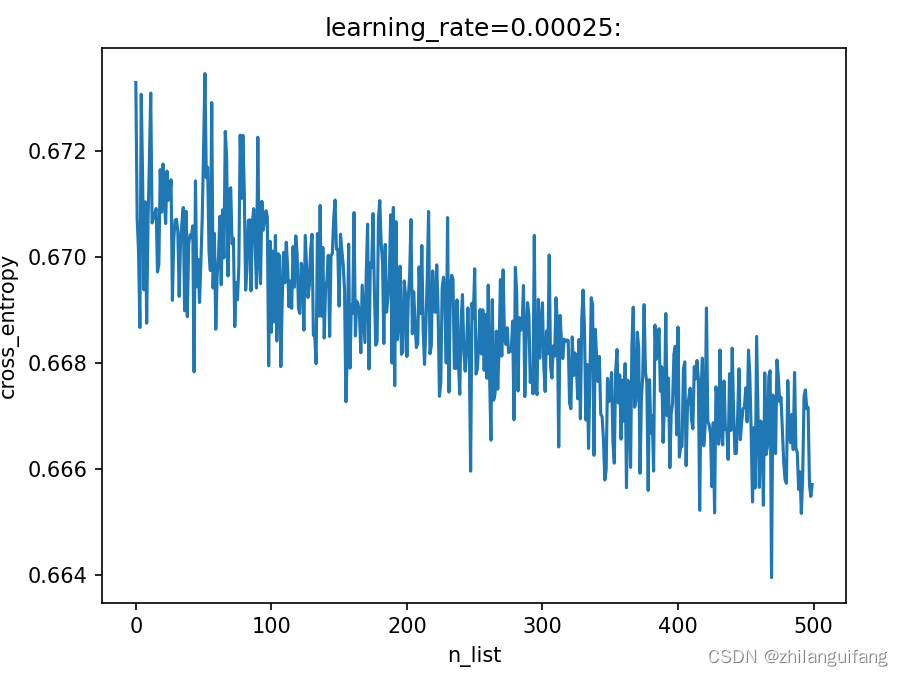
交叉熵越小，代表预测的值与实际分类距离越近，也就是预测效果越好。这个代价函数为什么一点都不平滑我也不清楚。emmmmmm……

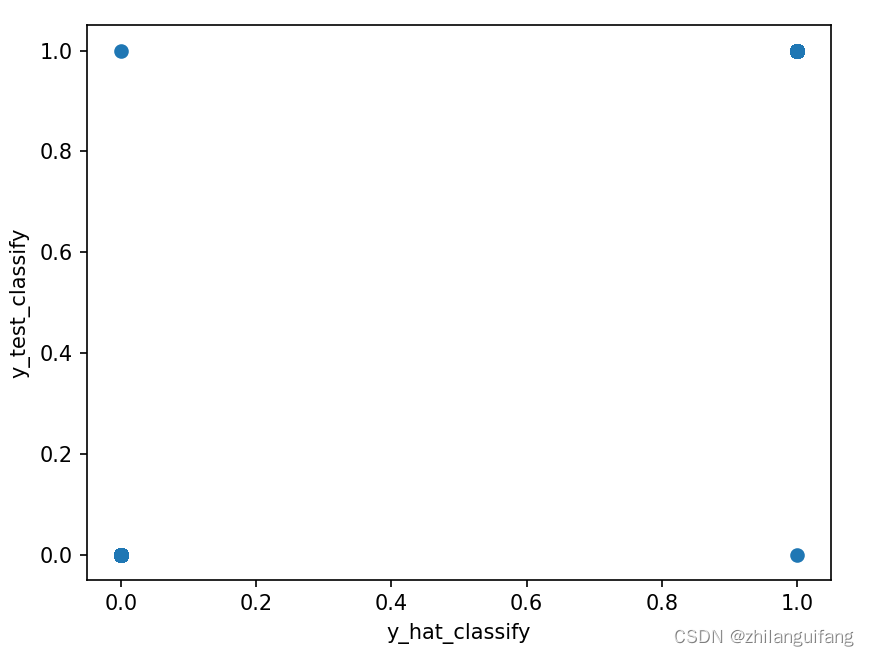
横坐标为预测分类，纵坐标为实际分类，由图知分类还是比较均衡的？
最后，我们看看召回率、精确率、f1值怎么样。

嗯，这个效果还是不错的，召回率、精确率、f1都在0.98以上。
本次实验就做到这里了，感谢观看。
全部代码附在下面

-- coding:utf-8 --

“”"
作者：邓dan
日期：2022年10月22日
“”"
//An highlighted block
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

class Datapreprocess_and_algotithm:
def init(self):
self.data = pd.read_csv(“alcohol_dataset.csv”)
self.x_train=0
self.y_train=0
self.x_test=0
self.y_test=0
self.w=[]
self.b=0

def func01(self,name):for index, item in enumerate(self.data[name]):self.data[name][index] = (item - self.data[name].min()) / (self.data[name].max() - self.data[name].min())  # 最小最大归一化
def data_preprocess(self):# 进行数据预处理，主要是归一化self.func01("TEMP_AMB")self.func01("TEMP_FAC_MAX")self.func01("TEMP_FAC_MIN")self.func01("EYES")self.func01("ALCOHOL")def train_test_split(self):self.data = self.data.sample(frac=1).reset_index(drop=True)     #每次打乱数据的顺序# 划分测试集和训练集self.x_train = self.data.iloc[:200, :-1]self.y_train = self.data.iloc[:200, -1]self.x_test = self.data.iloc[200:, :-1]self.y_test = self.data.iloc[200:, -1]def logic_regression(self,n,price):"""批梯度下降迭代法:param n: 迭代次数:param price:学习率:return:"""# 开始写逻辑回归算法feature_num = self.data.shape[1] - 1for i in range(feature_num):                              # 初始化wself.w.append(0.1)self.w = np.mat(self.w)                          # 将列表转换为矩阵形式（1，5）self.b = -0.3ce_list = []                                        # 存储迭代过程中的均方误差值n_list = []for i in range(n):self.train_test_split()self.x_train = np.mat(self.x_train)                # 将训练数据集转换成矩阵形式（200，5）self.y_train = np.mat(self.y_train)y_hat = (np.dot(self.w, self.x_train.T) + self.b)y_hat = 1.0 + np.exp(-y_hat)                         # 计算预测值y_hat（1，200）y_hat = 1 / y_hatm = len(self.x_train)                                     # 计算训练集数量y_train_ = 1 - self.y_train                               ## 计算代价函数，这里为交叉熵y_hat_ = 1 - y_hatt1 = np.dot(np.log(y_hat), self.y_train.T)t2 = np.dot(np.log(y_hat_), y_train_.T)cross_entropy = -1 / m * (t1 + t2)cross_entropy = cross_entropy[0, 0]e = y_hat - self.y_train                                            # 计算代价函数关于w,b的偏导数v = np.mat(np.ones([1, m]))del_b = 1 / m * np.dot(v, e.T)del_w = 1 / m * np.dot(self.x_train.T, e.T)self.w = self.w - price * del_w.T * 2                              # 迭代w和bself.b = self.b - price * del_b * 2ce_list.append(cross_entropy)                                       # 将该次迭代中计算的交叉熵存入列表n_list.append(i)plt.figure()plt.plot(n_list, ce_list)plt.xlabel("n_list")plt.ylabel("cross_entropy")plt.title(f"learning_rate={price}:")plt.show()def assessment(self):y_hat = (np.dot(self.w, self.x_test.T) + self.b)# 计算预测值y_hat（1，200）y_hat = 1/(1.0 + np.exp(-y_hat))y_hat01 = list((np.array(y_hat[0][0])).flatten())# print("y_hat01 before classify:\n", y_hat01)for i in range(len(y_hat01)):           # 将预测值转换为概率if y_hat01[i] > 0.5:y_hat01[i] = 1else:y_hat01[i] = 0y_test01 = list(self.y_test)# print("predicted:\n", y_hat01)# print("true_label:\n",y_test01)pred = 0true = 0precision_num = 0recall_num = 0pred_p_num = 0true_p_num = 0for i in range(len(y_hat01)):pred = y_hat01[i]true = y_test01[i]if pred == true and pred == 1:  # 预测为阳性precision_num += 1if pred == true and true == 1:recall_num += 1if pred == 1:pred_p_num += 1if true == 1:true_p_num += 1precision_rate=0recall_rate=0if true_p_num == 0:print("error,true=0!")else:recall_rate = float(recall_num) / true_p_numprint("recall_rate:", recall_rate)if pred_p_num == 0:print("error,pred=0!")else:precision_rate = float(precision_num) / pred_p_numprint("precision_rate:", precision_rate)f1 = 2 * precision_rate * recall_rate / (precision_rate + recall_rate)print("f1=",f1)# 绘制散点图plt.figure()plt.scatter(y_hat01, y_test01)plt.xlabel("y_hat_classify")plt.ylabel("y_test_classify")plt.show()

d=Datapreprocess_and_algotithm()
d.data_preprocess()
d.logic_regression(500,0.00025)
d.assessment()

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！