【愚公系列】2023年08月 3D数学-三角函数

文章目录

• 前言
• 一、三角函数
• • 1.概念
  • 2.作用
  • 3.分类
  • • 3.1 直角三角形的三角函数
    • 3.2 任意一点三角函数
  • 4.三角函数相关公式
  • • 4.1 假设α为任意角，则有任意角的三角函数公式
    • 4.2 三角函数求导公式
    • 4.3 三角函数转化公式
    • 4.4 三角函数的万能公式
    • 4.5 两角和与差公式

前言

在数学中，函数是一种映射关系，它将一个集合中的元素映射到另一个集合中的元素。通常来说，一个函数由三个部分组成：输入、输出和规则。输入是指函数接收的变量或数值，输出是指函数根据规则计算后得到的结果，规则则是描述输入与输出之间关系的公式或算法。

例如，一个简单的函数可以表示为：f(x) = x^2。在这个函数中，x是输入变量，f(x)是输出，规则是将输入的值乘以自身再输出。因此，当x=2时，函数的输出为f(2) = 2^2 = 4。

函数的定义域是指所有可输入的值的集合，值域是指函数可能得到的所有输出值的集合。例如，在上面这个函数中，定义域可以是所有实数，而值域则是所有非负实数。

函数在数学中有广泛的应用，例如描述物理规律、统计数据、计算金融利率等等。

一、三角函数

1.概念

三角函数是以角度或弧度为主变量的周期函数，在数学、物理、工程等领域中都有广泛的应用。常见的三角函数包括正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数等。这些函数可以用三角形中的比率表示，因此被称为三角函数。

2.作用

三角函数在数学、工程、物理等领域中有着广泛的应用。

在数学中，三角函数是解析几何、微积分和代数学习中必须掌握的一部分。它们被用来描述射线、角度、圆和曲线的形状。

在物理中，三角函数被广泛应用于描述周期性现象，例如电波、机械振动和光的波动等，还可以用来解决声波、电磁波等方面的问题。

在工程中，三角函数被用于设计和分析机械、电气、计算机系统等，例如构建机器人、调整电路和优化程序等。

其他领域三角函数还被广泛应用于音乐、艺术、体育、天文学等领域。因此，学习和掌握三角函数对于理解和应用这些领域的知识都是必须的。

3.分类

三角函数可以分为三种：正弦函数、余弦函数和正切函数。它们都是以角度作为自变量，以对应的三角比值作为函数值。

1. 正弦函数：sin(x) = 对边/斜边，x为夹角度数，对边指的是夹角的对边长度，斜边指的是夹角所在直角三角形的斜边长度。

2. 余弦函数：cos(x) = 邻边/斜边，x为夹角度数，邻边指的是夹角的邻边长度，斜边指的是夹角所在直角三角形的斜边长度。

3. 正切函数：tan(x) = 对边/邻边，x为夹角度数，对边指的是夹角的对边长度，邻边指的是夹角的邻边长度。

除此之外，还有其中两种函数的倒数函数：余切函数和正割函数，分别定义为cot(x) = 1/tan(x)，sec(x) = 1/cos(x)。

3.1 直角三角形的三角函数

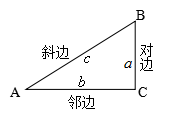
在直角三角形ABC中，其中ACB为直角。对BAC而言， 对边a=BC、斜边C=AB、邻边b=AC，则存在以下关系：

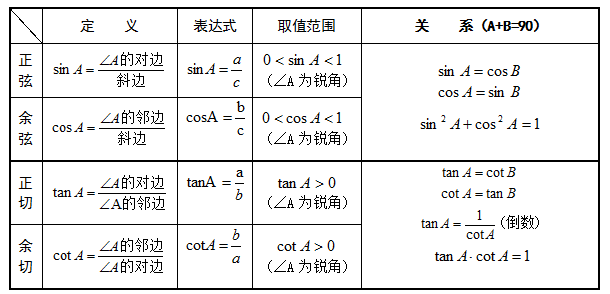
3.2 任意一点三角函数

对于任意一点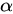对应的三条边分别为y、x、r。

常用的三角函数有正弦函数、余弦函数和正切函数。它们的定义如下：

正弦函数sin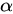 = y / r

余弦函数cos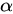 = x / r

正切函数tan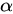 = y / x

同样的，我们也可以定义B、C对应的三角函数。

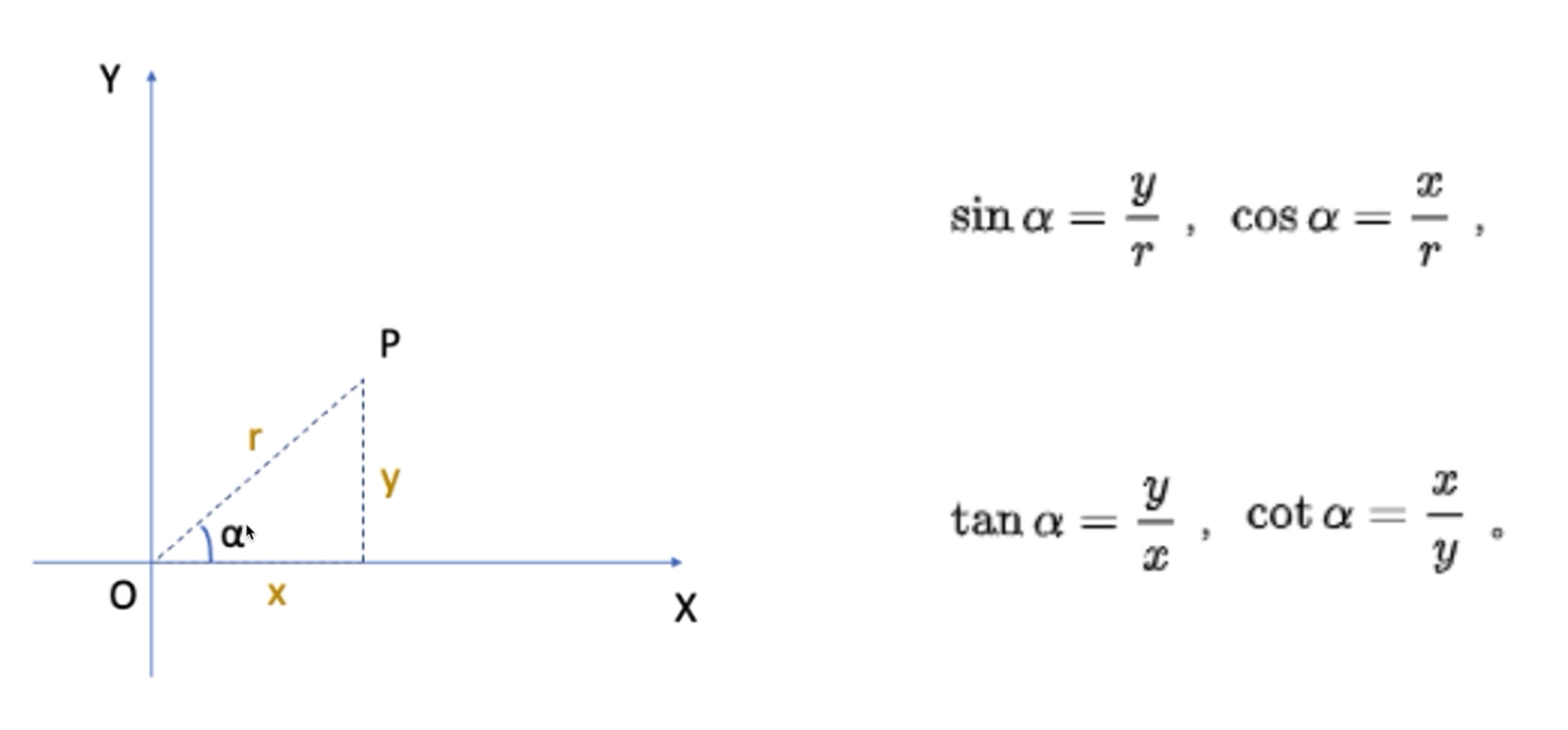
4.三角函数相关公式

4.1 假设α为任意角，则有任意角的三角函数公式

sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)

4.2 三角函数求导公式

正弦函数：(sinx)'=cosx余弦函数：(cosx)'=-sinx正切函数：(tanx)'=sec²x余切函数：(cotx)'=-csc²x正割函数：(secx)'=tanx·secx余割函数：(cscx)'=-cotx·cscx

4.3 三角函数转化公式

sin(-α)=-sinαcos(-α)=cosαsin(π/2-α)=cosαcos(π/2-α)=sinαsin(π/2+α)=cosαcos(π/2+α)=-sinαsin(π-α)=sinαcos(π-α)=-cosαsin(π+α)=-sinαtanα=sinα/cosαtan（π/2＋α）＝－cotαtan（π/2－α）＝cotαtan（π－α）＝－tanαtan（π＋α）＝tanα

4.4 三角函数的万能公式

sin(a)=[2tan(a/2)]/[1+tan2(a/2)]cos(a)=[1-tan2(a/2)]/[1+tan2(a/2)]tan(a)=[2tan(a/2)]/[1-tan2(a/2)]

4.5 两角和与差公式

两角和公式：对于任意一对角度 $\alpha$ 和 $\beta$，它们的正弦之和的公式为：
$$\sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta$$
余弦之和的公式为：
$$\cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$$
差公式：对于任意一对角度 $\alpha$ 和 $\beta$，它们的正弦之差的公式为：
$$\sin (\alpha -\beta )=\sin \alpha \cos \beta -\cos \alpha \sin \beta$$
余弦之差的公式为：
$$\cos (\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta$$
对于任意一对角度 $\alpha$ 和 $\beta$，它们的正切的和与差的公式如下：

正切的和的公式：
tan ⁡ ( α + β ) = tan ⁡ α + tan ⁡ β 1 − tan ⁡ α tan ⁡ β \tan(\alpha + \beta) = \frac{\tan\alpha + \tan\beta}{1-\tan\alpha\tan\beta} tan(α+β)=1−tanαtanβtanα+tanβ​

正切的差的公式：
tan ⁡ ( α − β ) = tan ⁡ α − tan ⁡ β 1 + tan ⁡ α tan ⁡ β \tan(\alpha - \beta) = \frac{\tan\alpha - \tan\beta}{1+\tan\alpha\tan\beta} tan(α−β)=1+tanαtanβtanα−tanβ​

需要注意的是，当 α ± β = π 2 + n π \alpha \pm \beta = \frac{\pi}{2} + n\pi α±β=2π​+nπ（其中 $n$ 为整数）时，公式中的分母会等于零，因此这些值无法通过这两个公式计算出来。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！