hdu 5047 Sawtooth(公式+JAVA大数)

Sawtooth

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 2794    Accepted Submission(s): 1047


Problem Description Think about a plane:

● One straight line can divide a plane into two regions.
● Two lines can divide a plane into at most four regions.
● Three lines can divide a plane into at most seven regions.
● And so on...

Now we have some figure constructed with two parallel rays in the same direction, joined by two straight segments. It looks like a character “M”. You are given N such “M”s. What is the maximum number of regions that these “M”s can divide a plane ?


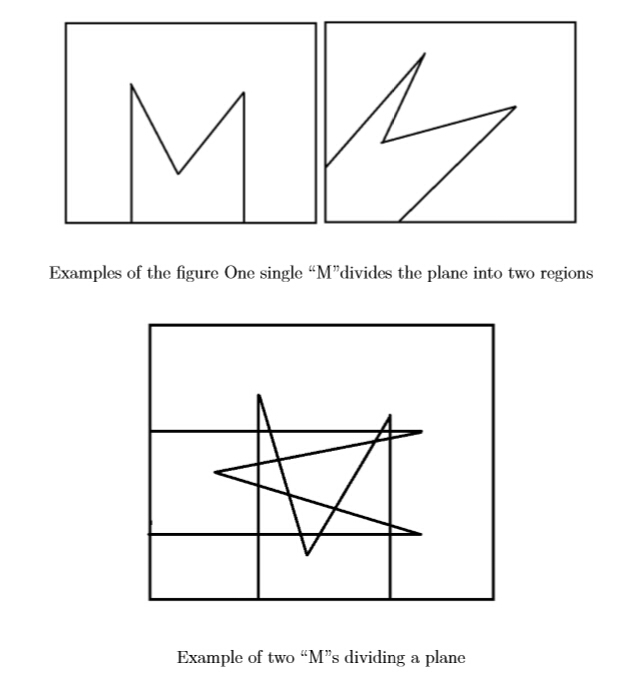
Input The first line of the input is T (1 ≤ T ≤ 100000), which stands for the number of test cases you need to solve.

Each case contains one single non-negative integer, indicating number of “M”s. (0 ≤ N ≤ 10 ¹²)
Output For each test case, print a line “Case #t: ”(without quotes, t means the index of the test case) at the beginning. Then an integer that is the maximum number of regions N the “M” figures can divide.
Sample Input

2 1 2
Sample Output

Case #1: 2 Case #2: 19
Source 2014 ACM/ICPC Asia Regional Shanghai Online
Recommend hujie

题意：

问n个'M'可以最多把平面划分成多少个平面。

思路：

先考虑一条线的情况，对于一条线容易想到，每次新增加的一条线都与原来的直线相交就可以产生更多的平面。得到

Cn = Cn-1 + n。

根据这个公式可以得到一个结论：

Cn = Cn-1 + n - 1 + 1

即下一个平面数可以由上一个平面数和新增加的直线的相交数+1来得到。

所以扩展到'M'形状，有4条直线，得到递推式为 

Cn = Cn-1 +16(n-1) +1

用累加法得到通项为 Cn = 8n^2 - 7n +1。

由于n会很大，用java大数类实现。

代码：

import java.util.Scanner;
import java.math.*;
public class Main{public static void main(String[] args){Scanner s = new Scanner (System.in);int t = s.nextInt();for(int i=1;i<=t;i++){BigInteger n=new BigInteger(s.next());BigInteger ans = n.multiply(n).multiply(new BigInteger("8")).subtract(n.multiply(new BigInteger("7"))).add(new BigInteger("1"));	System.out.println("Case #"+i+": "+ans);}
}
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！