用R语言模拟掷硬币过程

　　硬币分为Head(正面)和Tail(反面)，如果硬币是均匀的，那么出现Head和Tail的概率分别为50%、50%。把一枚硬币掷三次，结果有2*2*2=8种可能，分别为：
　　HHH、HHT、HTH、HTT
　　TTT、TTH、THT、THH
　　那么，样本空间(sample spaces): $\Omega$={HHH、HHT、HTH、HTT、TTT、TTH、THT、THH}，令$x$是$\Omega$里一个的样本，则
　　$P(x="HHH")=1/8$,
　　$P(x="HHT")=1/8$,
　　$...$
　　$P(x="THH")=1/8$
　　统计8个样本中H出现的次数:
　　　　Num(H)=3+2+2+1+0+1+1+2=8+4=12
　　那么H出现的频率为：
　　　　Frequency(H)= 12/(3*8)=12/24=0.5
　　可以看到P(H) = Frequency(H)
　　以上是从理论上分析的结果，在实际操作中，掷硬币三次，Num(H)可能为10，那么Frequent(H) = 10/24=0.41与0.5有较大的偏差。当我们把掷硬币的次数增加时，Frequent(H)会逐步接近0.5。下面，在RStudio中，使用R语言进行掷硬币的仿真实验。
　　//coin.R　　

# 掷硬币500次
N <- 500
flipsequence <- sample(x=c(0,1), prob=c(0.5,0.5),size = N, replace = TRUE)
r <- cumsum(flipsequence)
n <- 1:N
runprop = r/n#绘图
plot(n,runprop,type="o",log="x",xlim=c(1,N), ylim=c(0.0,1.0), cex.axis=1.5,main="Running Proportion of Heads",cex.axis=1.5)#添加一条直线y=0.5
lines(c(1,N),c(0.5,0.5),lty=3)#添加标注
flipletters <- paste(c("T","H")[flipsequence[1:10]+1], collapse = "")
displaystring <- paste("Flip Sequence= ", flipletters,'...',sep="" )
text(5,0.9, displaystring, adj = c(0,1),cex=1.3)
#显示模拟500次得到Head的频率
text(N-100,0.3, paste("End Proportion = ",runprop[N]),adj=c(1,0), cex=1.3)

　　效果如下：

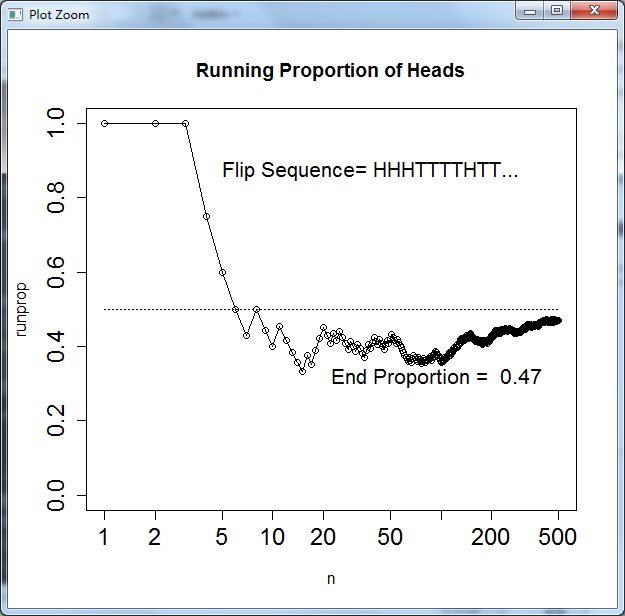
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！