从相关卷积到图像高斯模糊的快速计算
几年前的总结 ,在此记录一下:
一 相关
相关是用来衡量两个信号 "形状" 和 "相位"(起始位置)的相似程度 .
计算相关性的两个信号必须要有相同起始位置和长度,然后对两个信号逐点乘积加和,当两个信号完全一致时相关性是最高的.
离散信号相关计算定义:
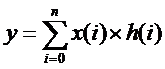
信号中的直流分量通常对信号表达是没有意义的,反而会产生干扰。所以某些相关性计算要先对信号做减直流处理,如数理统计里用协方差来度量相关性:
![]()
相关的计算是满足交换律的, "x 与 h的相关性" 等价于 "h与x的相关性" , 在这里我们把 h看成特征模板,x看成未知信号(下文卷积也都按这种约定).从这个角度来看
相关性计算也表达了"模板信号对未知信号加权和"的意思.比如要从一个很长的序列里匹配一段已知信号,相关计算算法可能从任意起始位置截取一段 x(0 ~ n) , 与 h 做加权和,得分最高的位置即是最匹配的信号.
二卷积(通常是指线卷积)
卷积与相关类似,按字面理解,先卷(与相关的主要区别),再积,离散卷积公式: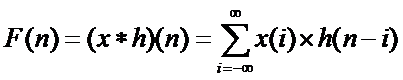
公式如下:
先把模板h翻卷(按原点对褶) h(i) -> h(-i)
h的零点对齐(平移) 到x的目标点n h(-i) -> h(n - i)
再对两段序列求逐点积,加和
当卷积模板中心对称时,卷积的结果与相关是一致的!!
同样的卷积计算满足交换率,即 (x * h)(n) <==> (h * x)(n)
卷积的物理解释:
a : 假如一幅只有不同黑色程度的水墨画下雨泡了水。 x(p) 表示水墨画在 p 点的含墨量,h(delta) 表示字画泡水后,单位墨向位置 (p + delta)扩散了多少 ( 实际扩散了 x(p) * h(p + delta) , 线性时不变系统) , 问题求是这幅画最终每一点的墨迹量。 注意, x 的定义域为整个画的二维坐标, h的定义域为与x,y平面原点中心对称的矩形区域。
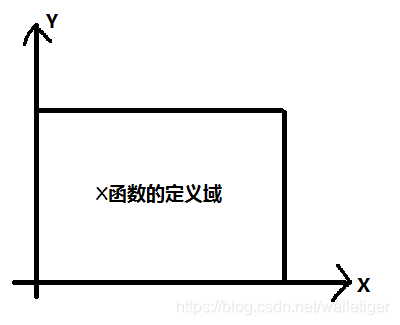
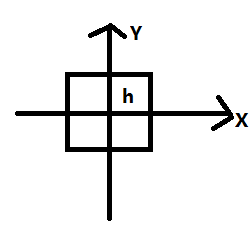
显然用卷积的定义求解就很容易, 目标点 P1受到模板h定义的所有邻域点影响,对于邻域点 Q1 , 位移了delta 到 P1 , 则 Q1 + delta = P1 ,即受Q1的影响为 x(Q1) * h (P1 - Q1) , p1 点收到总的影响为:
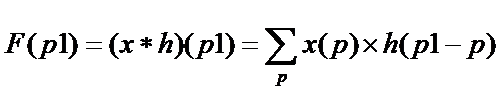
b : 假如小明在t时刻脸被挨打强度为x(t), 受单位强度的力挨打后, 脸鼓起的包随时间变化函数为 h(t) , 那问题来了, 求{0 , ... N}任意时刻小明脸鼓起的包强度。 显然 x(t) 和h(t) 的定义域只有时间正轴,包括零点。
信号里 x 被称为冲激函数, h 为冲激响应,这里冲激函数只会对后面的时刻产生响应。挨打之前脸上就有包那是不负责任的! 同样计算公式如下:
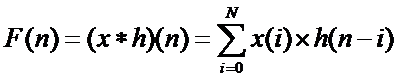
卷积计算的几种方法:
a 按公式 反褶(与零点)、平移(h 0点到目标位置n) , 逐点乘积 再求和
b 多项式方法(竖式计算法则)一种快捷计算方式
X1 = ![]()
X2 = ![]()
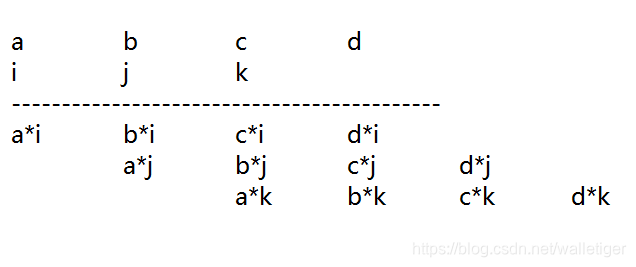
![]()
如图所示,竖式计算时,两个序列要做到齐次项对齐,即定义域零点对齐。
三圆周卷积
圆周卷积也称作循环卷积,百度百科里的定义如下图:
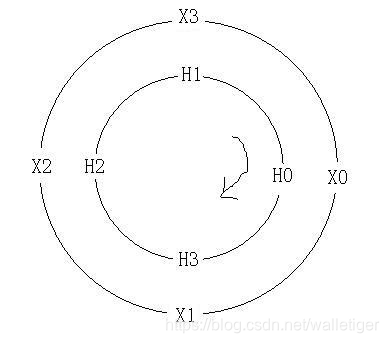
两个序列x,h (序列下标从0开始) , 作L点的圆周卷积:
1 首先将x ,h补成L长度的序列(少则补0,多则截断)
2 模板序列h逆时针排成一圈,x 顺时针排成一圈
3 求 0 点的圆周卷积对应位置相乘加和
4 求 点n 的圆周圈积,将模板h 顺时针转n下,再逐点乘积求和。
也来个定义:
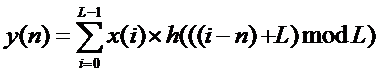
假设两个序列长度分别为 M,N , L >= M + N - 1 时 圆周卷积和线性卷积值是一致的!!
圆周卷积求法2: 竖式计算
X = {1 , 4 , 3 } , H = {1 , 2 , 3}
方法是用H的每一个元素去乘 X 每一组顺时针循环移位的序列,再求和:
1 X {1 , 4 , 3} + 2 X {3 , 1 , 4} + 3 X {4 , 3 , 1} = 1 4 3
6 2 8
12 9 3
---------------------------------
19 15 14
圆周卷积求法3: 矩阵乘法
X = {1 , 4 , 3 } , H = {1 , 2 , 3}
0
先将 H周期延拓(1,2,3 , 1,2,3 , 1,2,3),沿0点反转 , 再依次求每组顺时针循环右称的序列
HM =
| 1 3 2 |
| 2 1 3 |
| 3 2 1 |
F列向量 = ![]() = {19 , 15 , 14}
= {19 , 15 , 14}
圆周卷积求法4: DFT
经证明圆周卷积与 两个序列先DFT再乘积再逆DFT结果是一致。个人理解圆周卷积只是计算上有DFT 这种快速算法,没有线卷积那么强的物理意义,L = N + M - 1 时二者实现了统一。 L < N + M - 1 时会造成混叠效应。
四 利用圆周卷积来计算线性卷积
4.1 模板定义域为正轴数据
a 将 x & h 扩展成 L = N + M - 1 序列
b 计算圆周卷积。
c 再截掉 最后 2 *floor(M / 2) = M - 1个值
4.2 模板h定义域包含负值
这里举一个 h 中心对称的例子,同样 x 序列长度为N , h 长度为M M为奇数, 且h 定义域为 [ -M / 2 , M/ 2]
a 将包含负值的定义域平移到0点变成 [0 , M],这样最终卷积的结果会延时(晚) floor(M/2) 个点!
b 将 x & h 扩展成 L = N + M - 1 序列
c 计算圆周圈积。
4 截掉最前面 floor(M / 2) 和最后 (M / 2) 个点
4.3 线卷积matlab 代码
function [s] = linear_cov(x , h)N = size(x , 2);
M = size(h , 2);
L = N + M - 1;% fprintf(2 , 'M = %d , N = %d , L = %d \n' , M , N , L);s = zeros(1 , L);for i=1:Nfor j=1:Ms(j + i - 1) = s(j + i - 1) + x(i) * h(j);end
end 测试:
X=[4,5,6,7,8,9,10];
H=[1,2,3];
s=linear_cov(X,H);
%s=conv(H,X);4.4 圆周卷积matlab 代码
function [s] = circle_cov(x , h , L)N = size(x , 2);
M = size(h , 2);if N < L X1 = [x , zeros(1 , L - N)];
elseX1 = x(1:L);
endif M < LH1 = [h , zeros(1 , L - M)];
elseH1 = h(1:L);
ends = zeros(1 , L);for i=1:Lfor j=1:Ls(i) = s(i) + X1(j) * H1(1 + mod(i - j , L));end
end测试:
X=[4,5,6,7,8,9,10];
H=[1,2,3];
s=circle_cov(X,H , 9);
9点的圆周卷积结果与线卷积一致。
五 FFT 快速卷积
求x, h的卷积 matlab 代码: ( h (x) : x >= 0)
function [s] = fft_cov(x , h)N = size(x , 2);
M = size(h , 2);
L = N + M - 1;X = [x , zeros(1 , L - N)];
H = [h , zeros(1 , L - M)];f_x = fft(X);
f_h = fft(H);f_s = f_x .* f_h;
s = ifft(f_s);如果 h 定义域 x ![]() [-a , b] , a < 0 , 卷积输出会延时 a 长度。 对于二维图像卷积适用。
[-a , b] , a < 0 , 卷积输出会延时 a 长度。 对于二维图像卷积适用。
六 IIR 型高斯滤波器
参考:
https://www.cnblogs.com/luo-peng/p/5223910.html
IIR 型高斯滤波器特点是计算复杂度与 核 大小无关有一定参考意义
实现代码
//iir_guass_blur.h#ifndef __IIR_GUASS_BLUR_H
#define __IIR_GUASS_BLUR_H#ifdef __cplusplus
extern "C"
{
#endiflong IIR_guass_filter_create(int w , int h , float sigma);void IIR_guass_filter_do(long h_flt , const uint8_t * src_plane , int src_pitch , uint8_t *dst_plane , int dst_pitch);void IIR_guass_filter_destroy(long h_flt);long IIR_guass_filterI_create(int w , int h , float sigma);void IIR_guass_filterI_do(long h_flt , const uint8_t * src_plane , int src_pitch , uint8_t *dst_plane , int dst_pitch);void IIR_guass_filterI_destroy(long h_flt);#ifdef __cplusplus
}
#endif#endif
//iir_guass_blur.c#include
#include
#include
#include
#include
#include
#include "iir_guass_blur.h"/* *** IIR guass blur formula : **** * forward pass : w[n] = B * x[n] + (b1 * y[n - 1] + b2 * y[n - 2] + b3 * y[n - 3]) / b0;* backword pass :out[n] = B * w[n] + (b1 * out[n + 1] + b2 * out[n + 2] + b3 * out[n + 3]) / b0;* B = 1 - (b1 + b2 + b3) / b0; *
*/typedef struct IIR_guass_coefs
{float B;float b[4];
}IIR_guass_coefs;typedef struct IIR_guass_flt_context
{IIR_guass_coefs coeff;int w;int h;float sigma;float *w1;float *w2;uint8_t *dst_1pass;
}IIR_guass_flt_context;static void compute_coefs3(IIR_guass_coefs *c , float sigma)
{ float q, q2, q3; if (sigma >= 2.5){ q = 0.98711 * sigma - 0.96330; } else if ((sigma >= 0.5) && (sigma < 2.5)){ q = 3.97156 - 4.14554 * (float) sqrtf ((float) 1 - 0.26891 * sigma); } else { q = 0.1147705018520355224609375; } q2 = q * q; q3 = q * q2; c->b[0] = 1/(1.57825+(2.44413*q)+(1.4281 *q2)+(0.422205*q3)); c->b[1] = ( (2.44413*q)+(2.85619*q2)+(1.26661 *q3)) *c->b[0]; c->b[2] = ( -((1.4281*q2)+(1.26661 *q3)))*c->b[0]; c->b[3] = ( (0.422205*q3)) *c->b[0]; c->B = 1.0-(c->b[1]+c->b[2]+c->b[3]);
} long IIR_guass_filter_create(int w , int h , float sigma)
{IIR_guass_flt_context *ctx;int max_len;ctx = (IIR_guass_flt_context *)calloc(1 , sizeof(IIR_guass_flt_context));assert(ctx != NULL);ctx->w = w;ctx->h = h;ctx->sigma = sigma;compute_coefs3(&ctx->coeff , sigma);max_len = w > h ? w + 3 : h + 3;ctx->w1 = (float *)malloc(sizeof(float) * max_len);ctx->w2 = (float *)malloc(sizeof(float) * max_len);assert(ctx->w1 != 0);assert(ctx->w2 != 0);ctx->dst_1pass = (uint8_t *)malloc(sizeof(uint8_t) * h * w);assert(ctx->dst_1pass != 0);return (long)ctx;} void IIR_guass_filter_onepass( IIR_guass_flt_context *ctx , int width , int height , const uint8_t * src_plane , int src_pitch , uint8_t *dst_plane , int dst_pitch)
{const uint8_t *p_src;uint8_t *p_dst;int n , h;float *w1 , *w2 , *b , B;p_src = src_plane;p_dst = dst_plane;w1 = ctx->w1;w2 = ctx->w2;b = ctx->coeff.b;B = ctx->coeff.B;for(h = 0 ; h < height ; ++h){/*forward process*/w1[0] = w1[1] = w1[2] = p_src[0];for(n = 3 ; n < width + 3 ; ++n){w1[n] = B * p_src[n - 3] + b[1] * w1[n - 1] + b[2] * w1[n - 2] + b[3] * w1[n - 3];}/*backward process*/w2[width] = w2[width + 1] = w2[width + 2] = w1[width + 2];for(n = width - 1; n >= 0 ; --n){w2[n] = B * w1[n + 3] + b[1] * w2[n + 1] + b[2] * w2[n + 2] + b[3] * w2[n + 3];}/*store data*/for(n = 0 ; n < width ; ++n){p_dst[n * dst_pitch] = w2[n];}p_src += src_pitch;p_dst++;}
}void IIR_guass_filter_do(long h_flt , const uint8_t * src_plane , int src_pitch , uint8_t *dst_plane , int dst_pitch)
{IIR_guass_flt_context *ctx;ctx = (IIR_guass_flt_context *)h_flt;/*process horizontal data*/ IIR_guass_filter_onepass(ctx , ctx->w , ctx->h , src_plane , src_pitch , ctx->dst_1pass , ctx->h);/*process vertical data*/ IIR_guass_filter_onepass(ctx , ctx->h , ctx->w , ctx->dst_1pass , ctx->h , dst_plane , dst_pitch);}void IIR_guass_filter_destroy(long h_flt)
{IIR_guass_flt_context *ctx; ctx = (IIR_guass_flt_context *)h_flt;if (ctx->dst_1pass){free(ctx->dst_1pass);ctx->dst_1pass = 0;}if (ctx->w1){free(ctx->w1);ctx->w1 = 0;}if (ctx->w2){free(ctx->w2);ctx->w2 = 0;}free(ctx);
}typedef struct IIR_guass_coefsI
{int32_t B;int32_t b[4];
}IIR_guass_coefsI;typedef struct IIR_guass_fltI_context
{IIR_guass_coefsI coeff;int w;int h;float sigma;int32_t *w1;int32_t *w2;uint8_t *dst_1pass;
}IIR_guass_fltI_context;static void compute_coefs3_I(IIR_guass_coefsI *c , float sigma)
{ double q, q2, q3; if (sigma >= 2.5){ q = 0.98711 * sigma - 0.96330; } else if ((sigma >= 0.5) && (sigma < 2.5)){ q = 3.97156 - 4.14554 * (float) sqrtf ((float) 1 - 0.26891 * sigma); } else { q = 0.1147705018520355224609375; } q2 = q * q; q3 = q * q2; c->b[0] = 16384 / (1.57825+(2.44413*q)+(1.4281 *q2)+(0.422205*q3)); c->b[1] = ( (2.44413*q)+(2.85619*q2)+(1.26661 *q3)) * c->b[0]; c->b[2] = ( -((1.4281*q2)+(1.26661 *q3))) * c->b[0]; c->b[3] = ( (0.422205*q3)) * c->b[0]; c->B = 16384 - (c->b[1]+c->b[2]+c->b[3]);
} long IIR_guass_filterI_create(int w , int h , float sigma)
{IIR_guass_fltI_context *ctx;int max_len;ctx = (IIR_guass_fltI_context *)calloc(1 , sizeof(IIR_guass_fltI_context));assert(ctx != NULL);ctx->w = w;ctx->h = h;ctx->sigma = sigma;compute_coefs3_I(&ctx->coeff , sigma);max_len = w > h ? w + 3 : h + 3;ctx->w1 = (int32_t *)malloc(sizeof(int32_t) * max_len);ctx->w2 = (int32_t *)malloc(sizeof(int32_t) * max_len);assert(ctx->w1 != 0);assert(ctx->w2 != 0);ctx->dst_1pass = (uint8_t *)malloc(sizeof(uint8_t) * h * w);assert(ctx->dst_1pass != 0);return (long)ctx;} void IIR_guass_filterI_onepass( IIR_guass_fltI_context *ctx , int width , int height , const uint8_t * src_plane , int src_pitch , uint8_t *dst_plane , int dst_pitch)
{const uint8_t *p_src;uint8_t *p_dst;int n , h;int32_t *w1 , *w2 , *b , B;p_src = src_plane;p_dst = dst_plane;w1 = ctx->w1;w2 = ctx->w2;b = ctx->coeff.b;B = ctx->coeff.B;for(h = 0 ; h < height ; ++h){/*forward process*/w1[0] = w1[1] = w1[2] = p_src[0];for(n = 3 ; n < width + 3 ; ++n){w1[n] = B * p_src[n - 3] + b[1] * w1[n - 1] + b[2] * w1[n - 2] + b[3] * w1[n - 3];}/*backward process*/w2[width] = w2[width + 1] = w2[width + 2] = (w1[width + 2] >> 14);for(n = width - 1; n >= 0 ; --n){w2[n] = (B * (w1[n + 3] >> 14)) + b[1] * w2[n + 1] + b[2] * w2[n + 2] + b[3] * w2[n + 3];}/*store data*/for(n = 0 ; n < width ; ++n){p_dst[n * dst_pitch] = (w2[n] >> 14);}p_src += src_pitch;p_dst++;}
}void IIR_guass_filterI_do(long h_flt , const uint8_t * src_plane , int src_pitch , uint8_t *dst_plane , int dst_pitch)
{IIR_guass_fltI_context *ctx;ctx = (IIR_guass_fltI_context *)h_flt;/*process horizontal data*/ IIR_guass_filterI_onepass(ctx , ctx->w , ctx->h , src_plane , src_pitch , ctx->dst_1pass , ctx->h);/*process vertical data*/ IIR_guass_filterI_onepass(ctx , ctx->h , ctx->w , ctx->dst_1pass , ctx->h , dst_plane , dst_pitch);}void IIR_guass_filterI_destroy(long h_flt)
{IIR_guass_fltI_context *ctx; ctx = (IIR_guass_fltI_context *)h_flt;if (ctx->dst_1pass){free(ctx->dst_1pass);ctx->dst_1pass = 0;}if (ctx->w1){free(ctx->w1);ctx->w1 = 0;}if (ctx->w2){free(ctx->w2);ctx->w2 = 0;}free(ctx);
}
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!