吴恩达MachineLearning-Week3

原笔记网址：https://scruel.gitee.io/ml-andrewng-notes/week1.html

红色字体为自己的标注、绿色字体为自己的感想。

目录

6 逻辑回归(Logistic Regression)

• 6.1 分类(Classification)
• 6.2 假设函数表示(Hypothesis Representation)
• 6.3 决策边界(Decision Boundary)
• 6.4 代价函数(Cost Function)
• 6.5 简化的成本函数和梯度下降(Simplified Cost Function and Gradient Descent)
• 6.6 进阶优化(Advanced Optimization)
• 6.7 多类别分类: 一对多(Multiclass Classification: One-vs-all)

7 正则化(Regularization)

• 7.1 过拟合问题(The Problem of Overfitting)
• 7.2 代价函数(Cost Function)
• 7.3 线性回归正则化(Regularized Linear Regression)
• 7.4 逻辑回归正则化(Regularized Logistic Regression)

6 逻辑回归(Logistic Regression)

6.1 分类(Classification)

回顾一下，在监督学习中，有两种问题解决类型，分别是：回归与分类。对于结果为连续值的，我们使用回归算法。对于结果为离散型的，我们使用分类方法。

在分类问题中，预测的结果是离散值（结果是否属于某一类），逻辑回归算法(Logistic Regression)被用于解决这类分类问题。

• 垃圾邮件判断
• 金融欺诈判断
• 肿瘤诊断

我们不妨用肿瘤诊断举例，假设用线性回归的方法进行预测。用一条直线将y值划分。当y大于等于a时，y值为1；当y小于a时，y值为0.（0<=a<=1）可以发现，根本无法模拟得到理想的结果。因此，对于离散y值，我们不能采用线性回归的方法，于是考虑引入新的概念：分类。

区别于线性回归算法，逻辑回归算法是一个分类算法，其输出值永远在 0 到 1 之间。虽然名字中有回归两字，但那只是历史原因，仍然属于分类算法。

6.2 假设函数表示(Hypothesis Representation)

6.3 决策边界(Decision Boundary)

决策边界的概念，可帮助我们更好地理解逻辑回归模型的拟合原理。

回忆一下 sigmoid 函数的图像：

当然，通过一些更为复杂的多项式，还能拟合那些图像显得非常怪异的数据，使得决策边界形似碗状、爱心状等等。

简单来说，决策边界就是分类的分界线，分类现在实际就由 z(中的)决定啦。

记住：不是通过训练集得到的决策边界。而是通过训练集拟合得到，再由得到的决策边界。

我们只要让的方程等于零，就可以计算得到决策边界。但是要注意边界的哪个方向得到y=1，哪个方向又是y=0，不要弄混。

6.4 代价函数(Cost Function)

那我们怎么知道决策边界是什么样？多少时能很好的拟合数据？当然，见招拆招，总要来个 。

回忆线性回归中的平方损失函数，其是一个二次凸函数（碗状），二次凸函数的重要性质是只有一个局部最小点即全局最小点。而上图中有许多局部最小点，这样将使得梯度下降算法无法确定收敛点是全局最优（由于分类方法中h(x)是一个较复杂的函数，而非线性回归中的线性函数）。

如果令此处的损失函数是一个凸函数，则可以只有一个局部最小点即全局最小点，从而最优化。这类讨论凸函数最优值的问题，被称为凸优化问题(Convex optimization)。

当然，损失函数不止平方损失函数一种。

对于逻辑回归，更换平方损失函数为对数损失函数，可由统计学中的最大似然估计方法推出代价函数 ：

如左图，当训练集的结果为y=1（正样本）时，随着假设函数趋向于1，代价函数的值会趋于0，即意味着拟合程度很好。如果假设函数此时趋于0，则会给出一个很高的代价，拟合程度差，算法会根据其迅速纠正值，右图y=0同理。

区别于平方损失函数，对数损失函数也是一个凸函数，但没有局部最优值。

6.5 简化的成本函数和梯度下降(Simplified Cost Function and Gradient Descent)

由于懒得分类讨论，对于二元分类问题，我们可把代价函数简化为一个函数：

其中，在梯度下降优化的过程中，为了确保学习速率的适当以及保证梯度下降方法的有效运行，我们通过将代价函数与迭代次数为坐标轴画图。当代价函数随着迭代次数逐渐减小最后趋于稳定值，则当前学习速率适当，梯度下降有效运行。

相关例题如下：

补充：逻辑回归中代价函数求导的推导过程：

所以有：

则可得代价函数的导数：

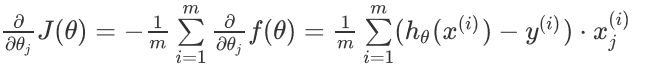
6.6 高级优化(Advanced Optimization)

运行梯度下降算法，其能最小化代价函数并得出的最优值，在使用梯度下降算法时，如果不需要观察代价函数的收敛情况，则直接计算的导数项即可，而不需要计算值。因为只需要利用到的导数项优化，得到最优值。从而最小化。

我们编写代码给出代价函数及其偏导数然后传入梯度下降算法中，接下来算法则会为我们最小化代价函数给出参数的最优解。这类算法被称为最优化算法(Optimization Algorithms)，梯度下降算法不是唯一的最小化算法1。

一些最优化算法：

• 梯度下降法(Gradient Descent)

• 共轭梯度算法(Conjugate gradient)

• 牛顿法和拟牛顿法(Newton's method & Quasi-Newton Methods)

  • DFP算法
  • 局部优化法(BFGS)
  • 有限内存局部优化法(L-BFGS)

• 拉格朗日乘数法(Lagrange multiplier)

比较梯度下降算法：一些最优化算法虽然会更为复杂，难以调试，自行实现又困难重重，开源库又效率也不一。不过这些算法通常效率更高，并无需选择学习速率 （少一个参数少一份痛苦啊！）。

Octave/Matlab 中对这类高级算法做了封装，易于调用。

下面为 Octave/Matlab 求解最优化问题的代码实例：

1. 创建一个函数以返回代价函数及其偏导数(注意是偏导而非完整的)：
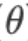2. 将 costFunction 函数及所需参数传入最优化函数 fminunc，以求解最优化问题：

   注：Octave/Matlab 中可以使用 help fminunc 命令随时查看函数的帮助文档。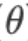

   注意：fminunc函数的参数至少要为二维。一维考虑使用fminuc。
3. 返回结果

6.7 多类别分类: 一对多(Multiclass Classification: One-vs-all)

一直在讨论二元分类问题，这里谈谈多类别分类问题（比如天气预报）。

原理是，转化多类别分类问题为多个二元分类问题，这种方法被称为 One-vs-all。

也就是说，对于一个输入x，判断其是哪一类（总共k类）。我们将把x分别带入k个假设函数，得到分别为这k个类别的概率，即为k维的。再找到最大的那个分量所对应的类别。则x是该类别的，问题解决。

7.1 过拟合问题(The Problem of Overfitting)

对于拟合的表现，可以分为三类情况：

• 欠拟合(Underfitting)

  无法很好的拟合训练集中的数据，预测值和实际值的误差很大，这类情况被称为欠拟合。拟合模型比较简单（特征选少了）时易出现这类情况。类似于，你上课不好好听，啥都不会，下课也差不多啥都不会。

• 优良的拟合(Just right)

  不论是训练集数据还是不在训练集中的预测数据，都能给出较为正确的结果。类似于，学霸学神！

• 过拟合(Overfitting)

  能很好甚至完美拟合训练集中的数据，即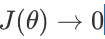，但是对于不在训练集中的新数据，预测值和实际值的误差会很大，泛化能力弱，这类情况被称为过拟合。拟合模型过于复杂（特征选多了）时易出现这类情况。类似于，你上课跟着老师做题都会都听懂了，下课遇到新题就懵了不会拓展。

线性模型中的拟合情况(左图欠拟合，右图过拟合)：

逻辑分类模型中的拟合情况：

为了度量拟合表现，引入：

• 偏差(bias)

  指模型的预测值与真实值的偏离程度。偏差越大，预测值偏离真实值越厉害。偏差低意味着能较好地反应训练集中的数据情况。(偏差是针对预测值与真实值之间的差值，因此偏差大代表欠拟合。)

• 方差(Variance)

  指模型预测值的离散程度或者变化范围。方差越大，数据的分布越分散，函数波动越大，泛化能力越差。方差低意味着拟合曲线的稳定性高，波动小。（方差是针对预测函数的波动。若函数过于复杂，波动剧烈，则方差大，出现过拟合。）

据此，我们有对同一数据的各类拟合情况如下图：

据上图，高偏差意味着欠拟合，高方差意味着过拟合。

我们应尽量使得拟合模型处于低方差（较好地拟合数据）状态且同时处于低偏差（较好地预测新值）的状态。

避免过拟合的方法有：

• 减少特征的数量

  • 手动选取需保留的特征
  • 使用模型选择算法来选取合适的特征(如 PCA 算法)
  • 减少特征的方式易丢失有用的特征信息

• 正则化(Regularization)

  • 可保留所有参数（许多有用的特征都能轻微影响结果）
  • 减少/惩罚各参数大小(magnitude)，以减轻各参数对模型的影响程度
  • 当有很多参数对于模型只有轻微影响时，正则化方法的表现很好

7.2 代价函数(Cost Function)

很多时候由于特征数量过多，过拟合时我们很难选出要保留的特征，这时候应用正则化方法则是很好的选择

（惩罚程度）正则化参数类似于学习速率，也需要我们自行对其选择一个合适的值。

• 过大（theta参数趋近于零）

  • 导致模型欠拟合(假设可能会变成近乎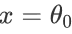的直线 )
  • 无法正常去过拟问题
  • 梯度下降可能无法收敛

• 过小（theta并没有缩小达到收敛的效果）

  • 无法避免过拟合（等于没有）

正则化符合奥卡姆剃刀(Occam's razor)原理。在所有可能选择的模型中，能够很好地解释已知数据并且十分简单才是最好的模型，也就是应该选择的模型。从贝叶斯估计的角度来看，正则化项对应于模型的先验概率。可以假设复杂的模型有较大的先验概率，简单的模型有较小的先验概率。

正则化是结构风险最小化策略的实现，是去过拟合问题的典型方法，虽然看起来多了个一参数多了一重麻烦，后文会介绍自动选取正则化参数的方法。模型越复杂，正则化参数值就越大。比如，正则化项可以是模型参数向量的范数。

7.3 线性回归正则化(Regularized Linear Regression)

应用正则化的线性回归梯度下降算法：

7.4 逻辑回归正则化(Regularized Logistic Regression)

为逻辑回归的代价函数添加正则化项：

而针对逻辑回归中更高级的算法，使用matlab内嵌函数求解，也只需更新相应的J,。

第一步写costFunction()中求J以及偏导，都要调用正则化更新后的式子，再使用fuminunc（）求得最小值。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！