分位数、箱线图

分位数：

根据其将数列等分的形式不同可以分为中位数、四分位数、十分位数、百分位数等等。

四分位数(Quartile)

将数据划分为4个部分，每部分大约包含1/4即25%的数据项，其临界点即为四分位数。

• Q1=第1四分位数，下分位数，即第25%分位数；
• Q2=第2四分位数，中位数，即第50%分位数；
• Q3=第3四分位数，上分位数，即第50%分位数；

四分位计算公式

n 1 = c o u n t / 4 n_1=count/4 n1​=count/4
m 1 = c o u n t % 4 m_1=count\%4 m1​=count%4
Q 1 = l i s t [ n 1 ] + ( l i s t [ n 1 + 1 ] − l i s t [ n 1 ] ) ∗ m 1 Q_1=list[n_1]+(list[n_1+1]−list[n_1])∗m_1 Q1​=list[n1​]+(list[n1​+1]−list[n1​])∗m1​

n 2 = 2 ∗ c o u n t / 4 n_2=2∗count/4 n2​=2∗count/4
m 2 = 2 ∗ c o u n t % 4 m_2=2∗count\%4 m2​=2∗count%4
Q 2 = l i s t [ n 2 ] + ( l i s t [ n 2 + 1 ] − l i s t [ n 2 ] ) ∗ m 2 Q_2=list[n_2]+(list[n_2+1]−list[n_2])∗m_2 Q2​=list[n2​]+(list[n2​+1]−list[n2​])∗m2​

n 3 = 3 ∗ c o u n t / 4 n_3=3∗count/4 n3​=3∗count/4
m 3 = 3 ∗ c o u n t % 4 m_3=3∗count\%4 m3​=3∗count%4
Q 3 = l i s t [ n 3 ] + ( l i s t [ n 3 + 1 ] − l i s t [ n 3 ] ) ∗ m 3 Q_3=list[n_3]+(list[n_3+1]−list[n_3])∗m_3 Q3​=list[n3​]+(list[n3​+1]−list[n3​])∗m3​

说明：其中 n、m 分别为整数部分和小数部分；list 代表数列，[] 表示索引取值；count 表示数列长度。

四分位差/内距/四分位间距（Inter-Quartile range）

I Q R = Q 3 − Q 1 IQR=Q_3−Q_1 IQR=Q3​−Q1​
指上分位数与下分位数之差。反映了中间 50% 数据的离散程度，数值越小说明中间的数据越集中，反之说明中间的数据越分散。

内限、外限、异常值

内限位于 Q 1 − 1.5 I Q R Q_1−1.5IQR Q1​−1.5IQR 和 Q 3 + 1.5 I Q R Q_3+1.5IQR Q3​+1.5IQR，
外限位于 Q 1 − 3 I Q R Q_1−3IQR Q1​−3IQR 和 Q 3 + 3 I Q R Q_3+3IQR Q3​+3IQR，
位于内限和外限之间的数据是中度异常值（mid outlier），位于外限以外的数据称为极端异常值（extreme outlier）。
该异常值检测方法叫Tukey’s method(图基)。

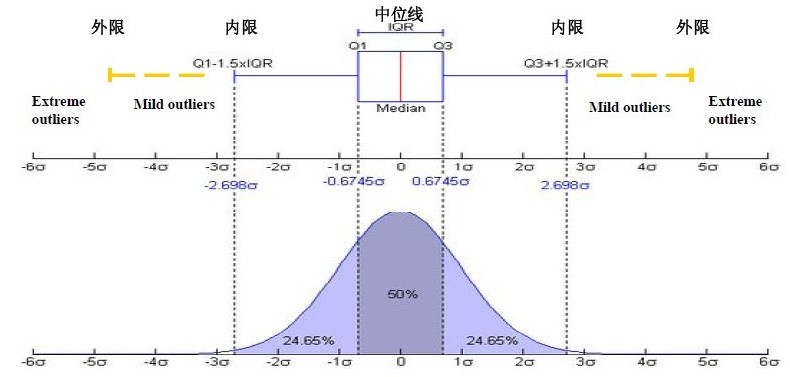
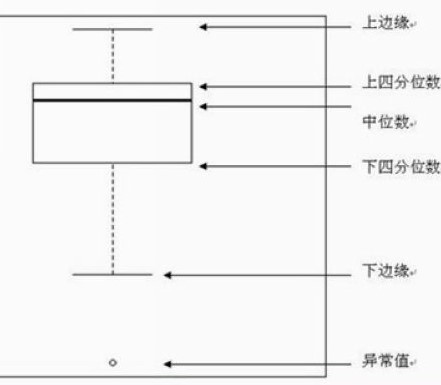
箱线图/箱须图（Boxplot/Box-whisker plot）

利用数据中的五个统计量：最小值、第一四分位数、中位数、第三四分位数与最大值来描述数据的一种方法，它也可以粗略地看出数据是否具有有对称性，分布的分散程度等信息，特别可以用于对几个样本的比较。 ——MBAlib 箱线图

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！