深度学习概念总结

深度学习概念总结

文章目录

• 深度学习概念总结
• 一、Dropout
• • 思想
  • 相关问题
  • • 为何Dropout能够解决过拟合
    • Dropout和Bagging有何不同
    • Dropout的缺陷
• 二、Normalization
• • 1、归一化
  • 2、归一化优点
  • 3、Batch Normalization
  • 4、Layer Normalization
  • 5、关于ICS
  • • ICS可能会导致什么问题
  • 6、BN和LN的选择
• 三、学习率衰减
• • 1、为什么要进行学习率衰减
  • 2、学习率衰减策略
• 四、提前终止
• 五、正则化
• • L1与L2具体内容
  • 为何只对权重惩罚
  • 权重衰减的目的
  • 为什么L1和L2可以防止过拟合
• 六、主动学习
• 七、偏差和方差
• • 如何降低偏差（欠拟合）
  • 如何降低方差（过拟合）
• 八、梯度消失，梯度爆炸
• • 解决方式
• 九、维数灾难问题
• 十、距离度量方法
• 十一、局部最小值，鞍点
• 十二、超参数调优
• 十三、深度学习项目流程

一、Dropout

思想

在每次训练过程中随机忽略一些神经元，正向传播对于下游神经元的贡献暂时消失，反向传播时也不会有任何权重的更新。
简单来说，Droopout通过参数共享，提供了一种廉价的Bagging集成近似，dropout策略相当于继承了包括所有从基础网络除去部分单元后形成的子网络。

相关问题

为何Dropout能够解决过拟合

“取平均”：dropout掉不同的隐藏神经元就类似在训练不同的网络（随机删除之后结构变化），整个dropout过程相当于对很多歌不同的神经网络取平均，不同的网络产生不同的过拟合，一些互为“反向”的拟合相互低消，就可以在整体上减少过拟合。

“减少共适应关系”：dropout程序导致两个神经元不一定每次都在一个dropout网络中出现，权值的更新不再依赖于有固定关系的隐含节点的共同作用，组织了某些特征仅仅在其他特定特征下才有效果的情况，让网络更加鲁棒。

综合来看就是神经网络不应该对一些特定的线索片段太过敏感，即使丢失特定的线索（神经元），也可以从其他线索（神经元）中学习一些共同的模式。

Dropout和Bagging有何不同

在Bagging的情况下，所有模型都是独立的，但是Dropout下，所有模型共享参数，每个模型集成父神经网络参数的不同子集。

在Bagging的情况下，每个模型都会在其相应训练集上训练到收敛，但是Dropout下，大部分模型通常没有显示地被训练，只是每次训练部分的子网络，参数共享使得剩余的子网络也能够有较好的参数设定。

Dropout的缺陷

dropout的缺点是代价函数J不再被明确定义，每次迭代都会少一些节点，如果多次检查梯度下降的性能，是不可观的。定义明确的代价函数J每次都会下降，但是在Dropout的网络中不太好计算。

解决这个问题的一种方式是：关闭dropout函数，将keep-prob的值设为1，运行代码，确保J函数单调递减。然后打开dropout函数，希望确认在dropout过程中，代码并未引入bug。

二、Normalization

1、归一化

min-max归一化：
当有新数据加入的时候，可能导致max和mn的变化，需要重新归一化数据，x = (x-min)/(max-min)

zero-mean归一化：
均值为0，标准差为1的正态分布。z-score标准化方法适用于属性A的最大值和最小值未知的情况，或者有超出取值范围的离群数据的情况。这种标准化方式要求原始数据的分布近似为高斯分布，否则效果会很差，x=(x-μ)/σ

以上两者的区别：
对于输出结果范围有要求——>使用min-max
数据较为稳定，不存在极端最大值和最小值——>归一化
数据存在异常值或者较多噪音——>标准化

2、归一化优点

归一化的本质就是线性变换，所以数据进行改变之后不会“失效”

归一化加快了梯度下降求最优解的速度

3、Batch Normalization

Batch Normalization（BN），就是在深度神经网络训练过程中使得每一层神经网络的输入保持相近的分布。
对于BN，在训练时，是对每一批的训练数据进行归一化，也即用每一批数据的均值和方差。而在测试时，比如进行一个样本的预测，就并没有batch的概念，因此，这个时候用的均值和方差是全量训练数据的均值和方差，这个可以通过移动平均法求得。
对于BN，当一个模型训练完成之后，它的所有参数都确定了，包括均值和方差，gamma和bata。因为用全量训练集的均值和方差容易过拟合，对于BN，其实就是对每一批数据进行归一化到一个相同的分布，而每一批数据的均值和方差会有一定的差别，而不是用固定的值，这个差别实际上能够增加模型的鲁棒性，也会在一定程度上减少过拟合。因此BN一般要求将训练集完全打乱，并用一个较大的batch值，否则，一个batch的数据无法较好得代表训练集的分布，会影响模型训练的效果。

优点：加速网络训练，抑制过拟合，降低了参数初始化的要求
缺点：对batch size的要求高，过小就无法估计出全局的样本分布。训练和预测时有区别，训练时一个batch之间进行Normalization，预测时需要依靠训练时获得的均值和方差进行预测。

“批规范化”：即在每次SGD时，通过mini-batch来对相应的activation做规范化操作，使得结果（输出信号各个维度）的均值为0，方差为1. 而最后的“scale and shift”操作则是为了让因训练所需而“刻意”加入的BN能够有可能还原最初的输入，从而保证整个network的capacity。

关于DNN中的normalization，大家都知道白化（whitening），只是在模型训练过程中进行白化操作会带来过高的计算代价和运算时间。因此本文提出两种简化方式：1）直接对输入信号的每个维度做规范化（“normalize each scalar feature independently”）；2）在每个mini-batch中计算得到mini-batch mean和variance来替代整体训练集的mean和variance. 这便是Algorithm 1.

4、Layer Normalization

LN 不同于 BN， 其在层内进行 Normalization， 即直接对隐层单元的输出做 Normalization。最大的好处是不再依赖 batch size。

通过第一节的分析，我们知道BN的两个缺点的产生原因均是因为计算归一化统计量时计算的样本数太少。LN是一个独立于batch size的算法，所以无论样本数多少都不会影响参与LN计算的数据量，从而解决BN的两个问题。
H是隐藏节点的数量，l是MLP的层数，可以计算LN的归一化统计量μ和σ


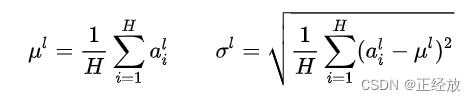
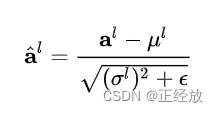
在LN中我们也需要一组参数来保证归一化操作不会破坏之前的信息，在LN中这组参数叫做增益（gain）g和偏置（bias）b。假设激活函数为f ，最终LN的输出为：

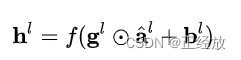
5、关于ICS

ICS指的是在训练过程中由于网络参数的变化而导致各层网络的输入分布发生了变化，而深层网络通过层层叠加，高层的输入分布变化会非常剧烈，这就需要高层不但去重新适应底层的参数更新。而为了训练好模型，需要非常谨慎地设定学习率、初始化权重等。
对于神经网络的各层输出，由于经过了一系列的因曾操作，分布显然与各层对应的输入数据分布不同，并且这种差距会随着网络深度的增加而加大。在训练过程中，网络参数的变化会让各层网络的输入分布发生变化，越深的网络，变化可能越大。

ICS可能会导致什么问题

上层参数需要不断适应新的输入数据分布，降低学习速度
下层输入的变化可能趋向于变大或变小，导致上层落入饱和区，使得学习过早停止。
每层的更新都会影响到其它层，因此每层的参数更新策略需要尽可能的谨慎。

6、BN和LN的选择

一般只在深层网络中使用， 比如在深层的 Transformer 中， LN 就起到了很关键的作用。
BN 与 LN 应用在非线性映射前效果更佳。
当你发现你的网络训练速度慢，梯度消失，爆炸等问题时， 不妨考虑加入 BN 或 LN 来试试。
使用 BN 时， 对 batch size 要求较高， 且在训练前需要对数据进行 shuffle。

BN 可以对第 L 层激活函数输出值或对第 L层激活函数的输入值进行 Normalization， 对于两个不同的位置，不少研究已经表明：放在第 L 层激活函数输出值会更好。

三、学习率衰减

1、为什么要进行学习率衰减

随着训练的加深，当模型训练到一定程度后，损失将不再减少，这个时候模型的一阶梯度接近于0， 对应的 Hessian 矩阵通常是两种情况：

• 正定，即所有特征值均为正，此时通常可以得到一个局部极小值，若这个局部极小值接近全局最小则模型已经能得到不错 的性能了，但若差距很大，则模型性能还有待于提升，通常情况下后者在训练初最常见。
• 特征值有正有负，此时模型很可能陷入了鞍点，若陷入鞍点，模型性能表现就很差。
  以上两种情况在训练初期以及中期，此时若仍然以固定的学习率，会使模型陷入左右来回的震荡或者鞍点，无法继续优化。所以，学习率衰减或者增大能帮助模型有效的减少震荡或者逃离鞍点。

2、学习率衰减策略

四、提前终止

提前终止的一种朴素的做法：当验证集的误差连续n次递增的时候停止训练，一般会将n设置为一个较大的数，跑一个较大的epoch，根据loss曲线来选择合适的epoch和n。

如何决定终止的时间，如果以验证集loss最小值作为保存模型的依据，
不一定就对泛化能力产生了影响，具体要看loss的曲线图，第一次跑的时候，往往会设置出一个很大的epoch，可以直观地从loss曲线上看到很多信息，帮助选择合适的epoch值，可以选取开始过拟合后多两步的epoch。

回到Trick， 文章谈到， 何时提前停止是对训练时间和泛化误差之间的权衡， 而如果我采用在验证集loss最低点存储模型的方式，那么何时提前停止就不再是对泛化误差的权衡了， 其变成了，如何选择何种的策略来对训练时间以及获取验证集loss全局最低点来做权衡，使得我们能够找到该点并保存模型，而不至于陷入一些困境。
最后谈谈 Early Stop 策略， 选择合适的策略能够使得我们在合适的时间终止整个训练，从而节省时间。

五、正则化

L1与L2具体内容

L2本质是参数解的2阶范数，以二维为例，L2的最优解就是一个圆；如果你还记得话，loss func的组成是两部分一部分是预测值和真实值之间的error，一部分是正则项，前一部分的解空间可以看作是一个梯度下降的等高线，这样一来，loss func的所有局部解就是每层等高线和这个圆之间的切点，所以说约束了解空间。这也是为啥L2会让解平滑，L1会让解稀疏（因为L1的解是一个四个顶点在坐标轴上的正方形，等高线与它的交点多半落在坐标轴上，意味着某一维会变成零）

为何只对权重惩罚

精确拟合偏置所需的数据通常比拟合权重少得多。每个权重会指定两个变量如何相互作用。我们需要在各种条件下观察这两个变量才能良好地拟合权重。而每个偏置仅控制一个单变量。这意味着，我们不对其进行正则化也不会导致太大的方差。另外，正则化偏置参数可能会导致明显的欠拟合。

权重衰减的目的

限制模型的学习能力，通过限制参数 θ 的规模（主要是权重 w 的规模，偏置 b 不参与惩罚），使模型偏好于权值较小的目标函数，防止过拟合。

为什么L1和L2可以防止过拟合

它们会使模型偏好于更小的权值，也就代表了更低的模型复杂度，对训练数据的拟合刚刚好，不会过分拟合训练数据，来提高模型的泛化能力
添加正则化相当于为模型添加了某种限制，规定了参数的分布，从而降低了模型的复杂度，复杂度越低，对于噪声和异常点的抗干扰性越强，提高模型的泛化能力（奥卡姆剃刀原理）

六、主动学习

思路：通过机器学习的方法获取那些比较难分类的样本数据，让人工再次确认和审核，然后将人工标注得到的数据再次使用有监督学习模型或者半监督学习模型进行训练，逐步提升模型效果，将人工校验融入机器学习的模型中。

增量学习的能力就是能够不断地处理现实世界中连续的信息流，在吸收新知识的同时保留甚至整合、优化旧知识的能力。

七、偏差和方差

偏差度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力；
方差度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响（模型的稳定性）；
噪声则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度。

偏差通常是由于我们定义的模型不合适或模型复杂度不够，所造成的现象为欠拟合。
方差主要是由于模型复杂度过高造成的， 所造成的现象是过拟合。

如何降低偏差（欠拟合）

1. 加大模型规模（更换其余机器学习算法，神经网络可以增加每层神经元/神经网络层数）：

2. 偏差很高很有可能是因为模型的拟合能力差，对于传统机器学习算法，各个方法的拟合能力不同，选择一个拟合能力更好的算法往往能够得出很好的结果。
   对于神经网络（拟合能力最强）而言，通过增加网络层数或增加每层单元数就能够很好的提高模型的拟合能力[3][4][5]。

3. 根据误差分析结果来修改特征：

   我们需要将错误样本分类，判断可能是由于什么原因导致样本失败，在针对分析结果，增加或减少一些特征。

4. 减少或去除正则化： 这可以避免偏差，但会增大方差。

5. 修改模型结构，以适应你的问题：对于不同的问题，不同的模型结构会产生更好的结果，比如在CV中常用CNN，而在NLP领域常用LSTM。

如何降低方差（过拟合）

1. 重新分析，清洗数据。

   有时候，造成方差很大的原因往往是由于数据不良造成的，对于深度学习来说，有一个大规模，高质量的数据集是极为重要的。

2. 添加更多的训练数据。

   增大训练数据能够往往能够提高模型的泛化能力。可以采用数据增强技术。

3. 加入正则化。

4. 加入提前终止。

   意思就是在训练误差变化很慢甚至不变的时候可以停止训练，这项技术可以降低方差，但有可能增大了偏差。
   提前终止有助于我们能够在到达最佳拟合附近，避免进入过拟合状态。

5. 通过特征选择减少输入特征的数量和种类。

   显著减少特征数量能够提高模型的泛化能力，但模型的拟合能力会降低，这意味着，该技术可以减小方差，但可能会增大偏差。
   不过在深度学习中，我们往往直接将所有特征放入神经网络中，交给算法来选择取舍。

6. 减少模型规模，降低模型复杂度（每层神经元个数/神经网络层数）： 谨慎使用。

   一般情况下，对于复杂问题如CV或NLP等问题不会降低模型复杂度，而对于简单问题，采用简单模型往往训练速度更快，效果很好。

7. 根据误差分析结果修改输入特征。

8. 修改模型架构，使之更适合你的问题。 一般可以选择简单模型的情况下，不选择复杂模型。

9. 集成学习。

八、梯度消失，梯度爆炸

如果在训练过程中发生了梯度消失，这也就意味着我们的权重无法被更新，最终导致训练失败。而梯度爆炸所带来的梯度过大，从而大幅度更新网络参数，造成网络不稳定（可以理解为梯度步伐太大）。在极端情况下，权重的值变得特别大，以至于结果会溢出（NaN值）

sigmoid函数的导数的最大值为1/4，通常我们会将权重初始值|w|初始化为为小于1的随机值，随着层数的增多，那么求导结果越小，这也就导致了梯度消失问题。

那么如果我们设置初始权重|w| 较大，那么会有|w*σ’|>1，造成梯度太大（也就是下降的步伐太大），这也是造成梯度爆炸的原因。

无论是梯度消失还是梯度爆炸，都是源于网络结构太深，造成网络权重不稳定，从本质上来讲是因为梯度反向传播中的连乘效应。

解决方式

1. 采用 Relu 系激活函数
2. 合适的权重初始化
3. 残差结构
4. Batch Normalization， Layer Normalization
5. 梯度裁剪 - 梯度爆炸
   如果梯度超过某个阈值，就对其进行限制。

九、维数灾难问题

当数据维度过高时，会为学习带来一些困难。

1. 数据稀疏：因为维数增多，样本密度必然减少
2. 样本分布不均匀：确的来说，处于中心位置的训练样本比边缘训练样本更加稀疏。
3. 过拟合问题：在高维中训练得到的分类器其实相当于低维空间上的一个复杂非线性分类器，而了解过拟合的同学都应该知道， 模型过于复杂往往是造成过拟合的直接原因。

如何解决维数灾难问题？

1. 对于数据稀疏与分布不均的问题，只有通过增加训练样本和降维的方式来解决。
2. 对于过拟合问题，可以添加针对过拟合的一些操作来解决。

十、距离度量方法

1. 欧式距离：衡量点之间的直线距离
2. 曼哈顿距离：各个维度差值绝对值的求和
3. 余弦距离：将两个点看做是空间中的两个向量，通过衡量两向量之间的相似性来衡量样本之间的相似性。
4. 切比雪夫距离：各对应坐标数值差的最大值。

十一、局部最小值，鞍点

局部最小值：
从数学的角度来说，局部最小值点首先满足一阶导数均为0， 我们还要保证曲线是凹的，也就是说，局部最小值点二阶导数均大于0。 总结来说，局部最小值满足两个条件：

鞍点：
对于所有参数的一阶导数均为0.
存在对于某一个参数，其二阶导数小于0.

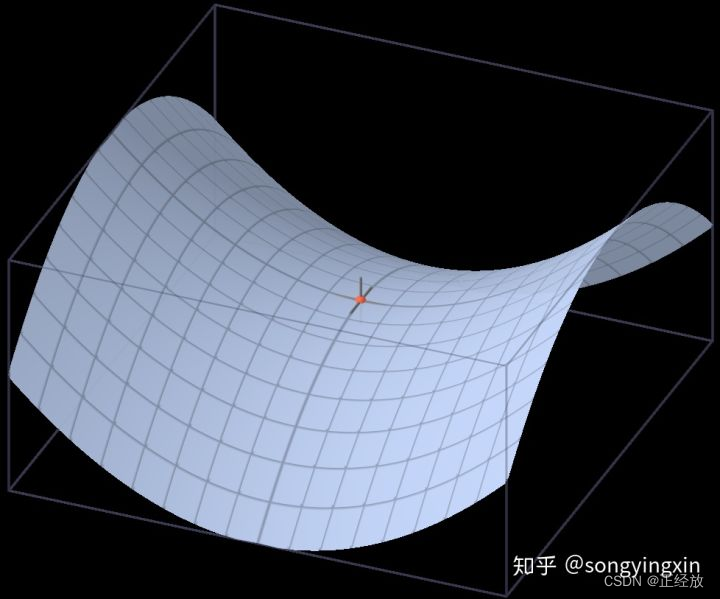
如何避免陷入局部最小值与鞍点？

1. SGD 或 Mini-batch：SGD 与 Mini-batch
   引入了随机性，每次以部分样本来计算梯度，能够相当程度上避免陷入局部最小值。
2. 动量：
   引入动量，相当于引入惯性。一些常见情况时，如上次梯度过大，导致进入局部最小点时，下一次更新能很容易借助上次的大梯度跳出局部最小点。
3. 自适应学习率：通过学习率来控制梯度是一个很棒的思想， 自适应学习率算法能够基于历史的累计梯度去计算一个当前较优的学习率。

十二、超参数调优

优化参数指的是反向传播中所涉及到的参数，主要包括：学习率， batch_size， 对应优化器参数， 损失函数参数等。

一般情况下， batch size 我往往会以 128 为起点，上下调整，注意，batch size 要设置为 2 的幂次方， 范围在 [1, 1024] 之间。

此外，需要一提的是 Batch Normalization 与 batch size 息息相关，如果你使用了 Batch Normalization， 那么 batch size 就不能设的太小， 这点我在 Normalization 那一节中有详细解释。

十三、深度学习项目流程

1. 定义问题
   确定是分类问题还是回归问题，还是无监督问题。
2. 探索和清洗数据
   探索和进一步清洗数据集一直都是深度学习中最重要的一步。
3. 选择模型并探索模型结果
   探索模型的结果，通常是需要对模型在验证集上的性能进行进一步的分析，这是如何进一步提升模型性能很重要的步骤。将模型在训练集和验证集都进行结果的验证和可视化，可直观的分析出模型是否存在较大偏差以及结果的正确性。
4. 监控训练和验证误差
   首先很多情况下，我们忽略代码的规范性和算法撰写正确性验证，这点上容易产生致命的影响。
   在训练和验证都存在问题时，首先请确认自己的代码是否正确。其次，根据训练和验证误差进一步追踪模型的拟合状态。若训练数据集很小，此时监控误差则显得格外重要。确定了模型的拟合状态对进一步调整学习率的策略的选择或者其他有效超参数的选择则会更得心应手。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！