电力电子技术笔记-整流电路5
电容滤波的不可控整流电路
在交—直—交变频器、不间断电源、开关电源等应用场合中，大量应用。
最常用的是单相桥和三相桥两种接法。
由于电路中的电力电子器件采用整流二极管，故也称这类电路为二极管整流电路。
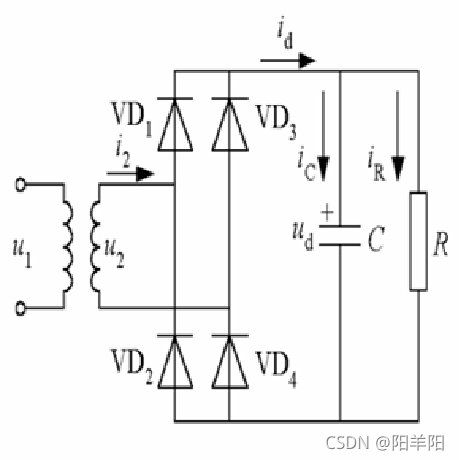
1、电容滤波的单相不可控整流电路
常用于小功率单相交流输入的场合，如目前大量普及的微机、电视机等家电产品中。
基本工作过程：
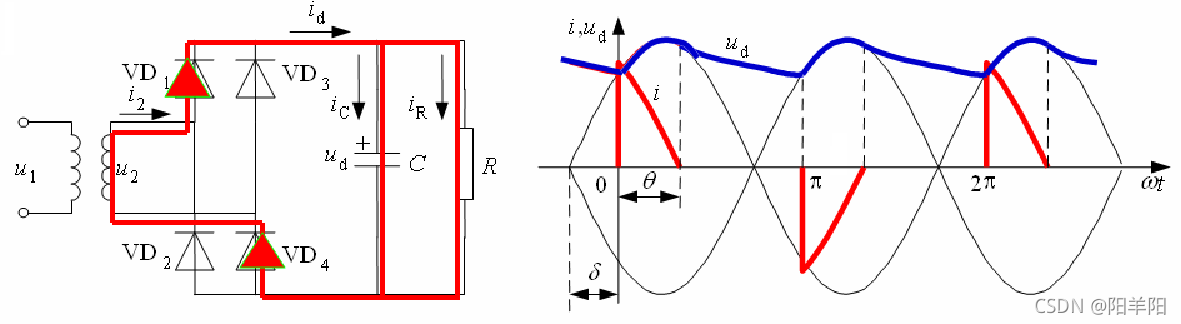
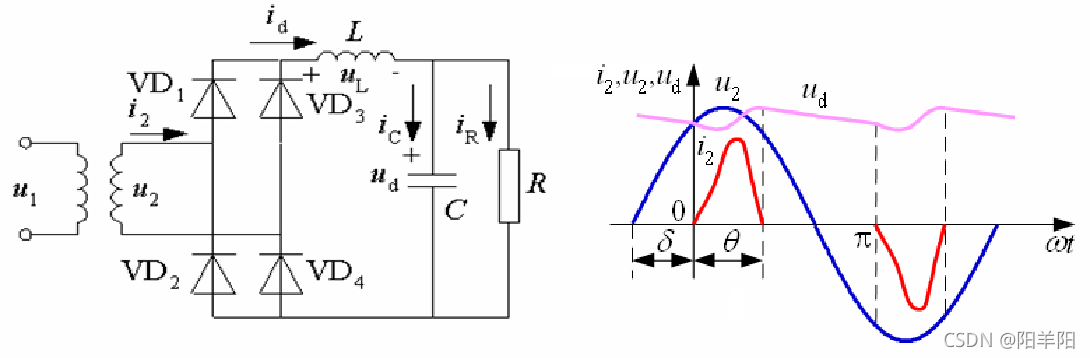
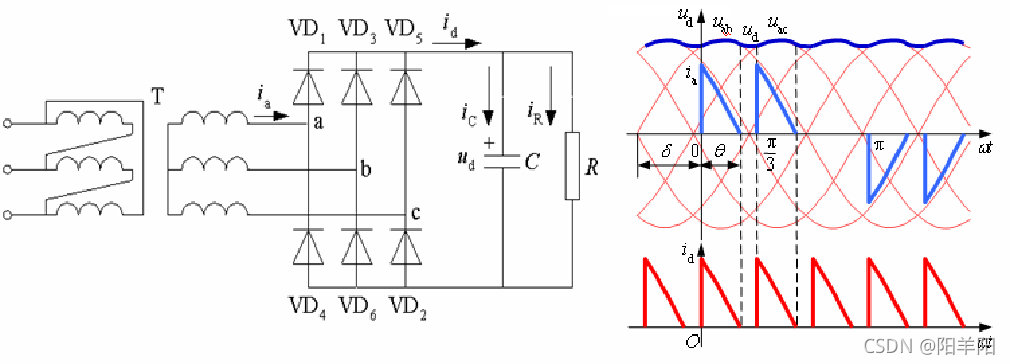
在u2 正半周过零点至wt=0期间，因u2 至wt=0 之后，u2 将要超过ud，使得VD1和VD4开通，ud=u2，交流电源向电容充电，同时向负载 R 供电。 主要的数量关系 输出电压平均值 空载时： 重载时， 在设计时，根据负载的情况选择电容C 值，使 此时输出电压为： 电流平均值 输出电流平均值IR为：IR = Ud /R Id = IR 二极管电流 iD平均值为：ID = Id / 2=IR/ 2 二极管承受的电压为： 实际广泛应用的电路：感容滤波的二极管整流电路 电路特点： ud波形更平直，电流i2的上升段平缓了许多，这对于电路的工作是有利的。 基本原理：某一对二极管导通时，输出电压等于交流侧线电压中最大的一个，该线电压既向电容供电，也向负载供电。 当没有二极管导通时，由电容向负载放电，ud按指数规律下降。 电流id 断续和连续的临界条件: 在轻载时,直流侧获得的充电电流是断续的： 在重载时，直流侧获得的充电电流是连续的： 主要数量关系 输出电压平均值: Ud 在（2.34U2 ~2.45U2）之间变化 电流平均值 输出电流平均值IR为： IR = Ud /R 与单相电路情况一样，电容电流iC平均值为零，则Id = IR 二极管电流平均值为Id的1/3，即： ID = Id / 3=IR/ 3 二极管承受的最大反向电压为线电压的峰值，即 随着电力电子技术的发展，其应用日益广泛，由此带来的谐波(harmonics)和无功(reactive power)问题日益严重，引起了关注。 1 、谐波和无功功率分析基础 谐波和功率因数的关系 电网施加给负载的电压为正弦信号，但负载从电网索取的电流是否也为正弦信号，则取决于负载是线性还是非线性的。 线性负载：如R,L,C等，电流为同频正弦波。 非线性负载：如电力半导体设备，尤其是常用的SCR整流， 电流变为非正弦信号。 基波与谐波：非正弦电流展开傅氏级数。 频率仍与工频相同的分量称为基波；频率为基波频率整数倍的分量称为谐波。 电流谐波总畸变率： 通常公用电网中的电压波形畸变很小，而电流波形畸变可能很大，故在分析中，将电压视为正弦，电流为非正弦，具有实际意义。 非正弦电路的有功功率 ： P = U I cosφ 功率因数为： 基波(畸变)因数—— 即基波电流有效值和总电流有效值之比 位移因数（基波功率因数）—— cosφ 功率因数由基波电流相移和电流波形畸变这两个因素共 同决定的。 1、单相桥式全控整流电路（阻感负载） 忽略换相过程和电流脉动，在大L-R(E)负载时，变压器副边电流 i2 为近似180°正负对称方波。 变压器二次侧电流谐波分析： 基波与各次谐波电流有效值之间关系为 功率因数计算 基波电流有效值为 i2的有效值 I = Id，结合上式可得基波因数为 电流基波与电压的相位差就等于控制角α，故位移因数为 则，功率因数为 2、三相桥式全控整流电路(阻感负载) L很大时，id近似恒流Id，ia比ua滞后角为 变压器二次侧电流谐波分析： 基波与各次谐波电流有效值为 功率因数计算 基波电流有效值为 基波因数为 位移因数为 则，功率因数为
，即接近电阻负载时的特性。
2、电容滤波的三相不可控整流电路
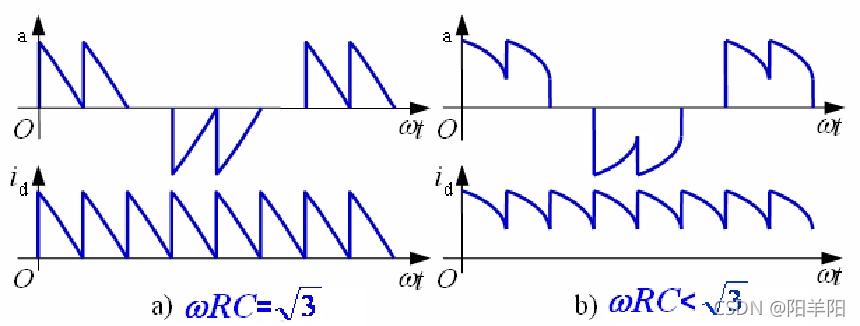
。整流电路的谐波和功率因数
---- 总谐波电流的有效值
---- 基波电流的有效值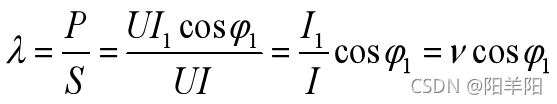
2 、阻感负载整流电路交流侧谐波和功率因数分析
n=1,3,5,…
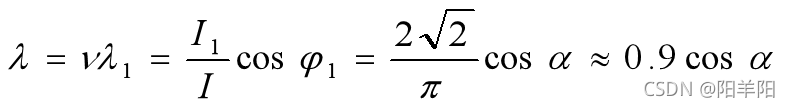
， ia为近似1200正负对称方波，总有效值为
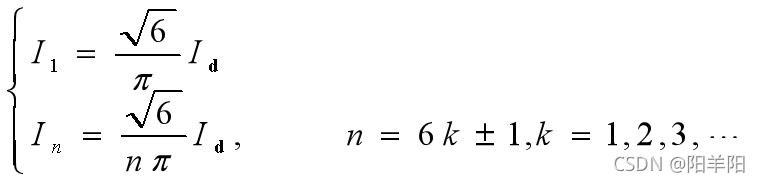
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！