Julia求解简谐振动的微分方程

文章目录

• • 简谐振动
  • SciML求解

简谐振动

简谐振动的方程为

x ¨ + ω x = 0 \ddot x+\omega x=0 x¨+ωx=0

解得

x ( t ) = A cos ⁡ ( ω t − ϕ ) v ( t ) = x ˙ ( t ) = − A ω sin ⁡ ( ω t − ϕ ) \begin{aligned} x(t)&=A\cos(\omega t-\phi)\\ v(t)&=\dot x(t) = -A\omega\sin(\omega t-\phi) \end{aligned} x(t)v(t)​=Acos(ωt−ϕ)=x˙(t)=−Aωsin(ωt−ϕ)​

SciML求解

通过SciML的求解代码如下，首先引入模块，并定义全局变量

using OrdinaryDiffEq, Plotsω = 1           #输入\omega然后按tab可打出ω
x₀ = [0.0]      #输入\_0 然后按tab可打出下标₀
dx₀ = [π/2]     #\pi tab
tspan = (0.0, 2π)ϕ = atan((dx₀[1]/ω)/x₀[1])
A = √(x₀[1]^2 + dx₀[1]^2)

接下来就是核心代码

#
function f(ddu,du,u,ω,t)ddu .= -ω^2 * u
end# 创建二阶ODE问题
prob = SecondOrderODEProblem(f, dx₀, x₀, tspan, ω)
sol = solve(prob, DPRKN6())#Plot
plot(sol, vars=[2,1], linewidth=2, title ="简谐振动", label = ["x" "dx"])
plot!(t->A*cos(ω*t-ϕ), lw=3, ls=:dash, label="解析解 x")
plot!(t->-A*ω*sin(ω*t-ϕ), lw=3, ls=:dash, label="解析解 dx")
savefig("ode_7.png")

结果如图所示

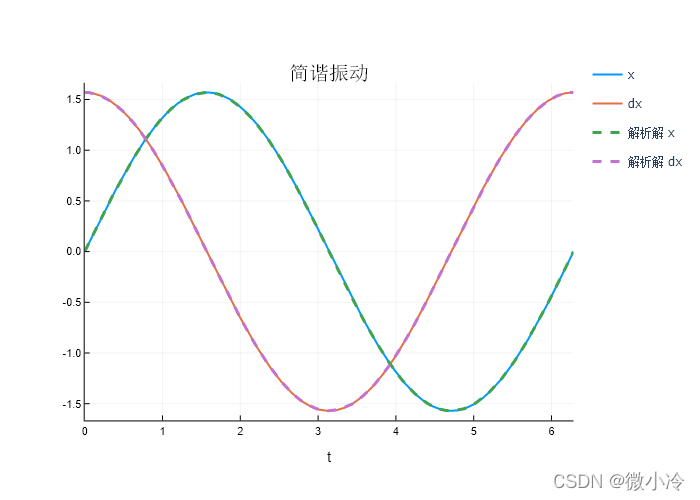
其中，DPRKN6是一个高效但不精确的求解器，采用的是龙格库塔法，并且具有6阶插值。如果感觉精度不够的话，可以改用DPRKN12，顾名思义有12阶插值，但相对来说会慢一些。

关于Runge-kutta法

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！