二阶电路的时域分析

目录

• 1. 零输入响应
• • （1）过阻尼
  • （2）欠阻尼
  • （3）临界状态
• 2. *零状态响应
• 3. *全响应

1. 零输入响应

以RLC电路为例

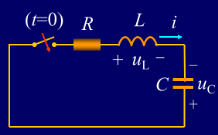
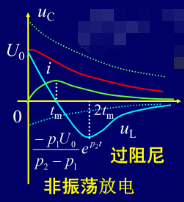
（1）过阻尼

u C = U 0 p 2 − p 1 ( p 2 e p 1 t − p 1 e p 2 t ) u_C = \frac{U_0}{p_2-p_1}(p_2e^{~p_1t} - p_1e^{~p_2t}) uC​=p2​−p1​U0​​(p2​e p1​t−p1​e p2​t)

i = − U 0 L ( p 2 − p 1 ) ( e p 1 t − e p 2 t ) i = -\frac{U_0}{L(p_2-p_1)}(e^{~p_1t} - e^{~p_2t}) i=−L(p2​−p1​)U0​​(e p1​t−e p2​t)

u L = − U 0 p 2 − p 1 ( p 1 e p 1 t − p 2 e p 2 t ) u_L = - \frac{U_0}{p_2-p_1}(p_1e^{~p_1t} - p_2e^{~p_2t}) uL​=−p2​−p1​U0​​(p1​e p1​t−p2​e p2​t)

t m = l n p 2 p 1 p 1 − p 2 t_m = \frac{ln\frac{p_2}{p_1}}{p_1-p_2} tm​=p1​−p2​lnp1​p2​​​

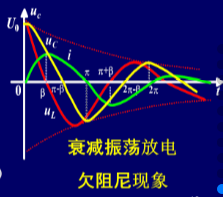
（2）欠阻尼

δ = R 2 L δ=\frac{R}{2L} δ=2LR​

ω = 1 L C − ( R 2 L ) 2 \omega=\sqrt{\frac{1}{LC} - (\frac{R}{2L})^2} ω=LC1​−(2LR​)2 ​

ω 0 : = ω 2 + δ 2 \omega_0: = \sqrt{\omega^2 +δ^2 } ω0​:=ω2+δ2 ​

β = a r c t a n ( ω δ ) \beta = arctan(\frac{\omega}{δ}) β=arctan(δω​)

u C = U 0 ω 0 ω e − δ t s i n ( ω t + β ) u_C = \frac{U_0\omega_0}{\omega}e^{-δt}sin(\omega t + \beta) uC​=ωU0​ω0​​e−δtsin(ωt+β)

i = U 0 ω L e − δ t s i n ( ω t ) i = \frac{U_0}{\omega L}e^{-δt}sin(\omega t) i=ωLU0​​e−δtsin(ωt)

u L = − U 0 ω 0 ω e − δ t s i n ( ω t − β ) u_L = -\frac{U_0\omega_0}{\omega}e^{-δt}sin(\omega t - \beta) uL​=−ωU0​ω0​​e−δtsin(ωt−β)

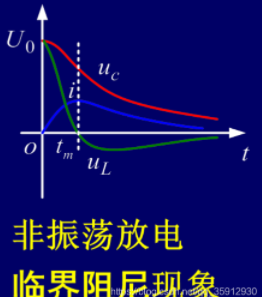
（3）临界状态

u C = U 0 ( 1 + δ t ) e − δ t u_C = U_0(1+δt)e^{-δt} uC​=U0​(1+δt)e−δt

i = U 0 L t e − δ t i = \frac{U_0}{L}te^{-δt} i=LU0​​te−δt

u L = U 0 e − δ t ( 1 − δ t ) u_L = U_0 e^{-δt}(1-δt) uL​=U0​e−δt(1−δt)

2. *零状态响应

列方程，求解

3. *全响应

列方程
求特解
求通解
定常数

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！