调和级数求和(打表/欧拉常数) - Harmonic Number LightOJ - 1234
调和级数求和(打表/欧拉常数) - Harmonic Number LightOJ - 1234
题意:
计 算 调 和 级 数 前 n 项 的 和 : 计算调和级数前n项的和: 计算调和级数前n项的和:
H n = 1 + 1 2 + 1 3 + . . . + 1 n = ∑ i = 1 n 1 i H_n=1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n}=\sum_{i=1}^n\frac{1}{i} Hn=1+21+31+...+n1=i=1∑ni1
Input
Input starts with an integer T (≤ 10000), denoting the number of test cases.
Each case starts with a line containing an integer n (1 ≤ n ≤ 108).
Output
For each case, print the case number and the nth harmonic number H n H_n Hn. Errors less than 10-8 will be ignored.
Sample Input
12
1
2
3
4
5
6
7
8
9
90000000
99999999
100000000
Sample Output
Case 1: 1
Case 2: 1.5
Case 3: 1.8333333333
Case 4: 2.0833333333
Case 5: 2.2833333333
Case 6: 2.450
Case 7: 2.5928571429
Case 8: 2.7178571429
Case 9: 2.8289682540
Case 10: 18.8925358988
Case 11: 18.9978964039
Case 12: 18.9978964139
T i m e l i m i t : 3000 m s , M e m o r y l i m i t : 32768 k B Time\ limit:3000 ms,Memory \ limit:32768 kB Time limit:3000ms,Memory limit:32768kB
分析:
方法一:打表
考 虑 到 空 间 限 制 , 1 0 8 组 数 据 不 能 够 全 部 打 出 来 , 考虑到空间限制,10^8组数据不能够全部打出来, 考虑到空间限制,108组数据不能够全部打出来,
但 可 以 每 隔 50 组 数 据 记 录 一 次 , 存 储 2 × 1 0 6 组 数 据 , 对 于 每 一 个 n , 再 做 一 个 50 次 以 内 的 递 推 。 但可以每隔50组数据记录一次,存储2×10^6组数据,对于每一个n,再做一个50次以内的递推。 但可以每隔50组数据记录一次,存储2×106组数据,对于每一个n,再做一个50次以内的递推。
方法二:欧拉常数
欧 拉 常 数 : 是 一 个 主 要 应 用 于 数 论 的 数 学 常 数 。 它 的 定 义 是 调 和 级 数 与 自 然 对 数 的 差 值 的 极 限 。 欧拉常数:是一个主要应用于数论的数学常数。它的定义是调和级数与自然对数的差值的极限。 欧拉常数:是一个主要应用于数论的数学常数。它的定义是调和级数与自然对数的差值的极限。
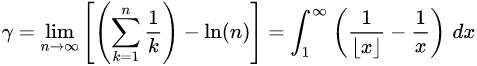
γ ≈ 0.57721566490153286060651209 。 γ≈0.57721566490153286060651209。 γ≈0.57721566490153286060651209。
渐进展开: γ = H n − l n n − 1 2 n + 1 12 n 2 − 1 120 n 4 + . . . γ=H_n-ln\ n-\frac{1}{2n}+\frac{1}{12n^2}-\frac{1}{120n^4}+... γ=Hn−ln n−2n1+12n21−120n41+...
故 当 n 较 大 时 , 我 们 可 近 似 计 算 H n = l n n + 1 2 n + γ 故当n较大时,我们可近似计算H_n=ln\ n+\frac{1}{2n}+γ 故当n较大时,我们可近似计算Hn=ln n+2n1+γ
由 于 本 题 误 差 在 1 0 8 数 量 级 , 故 当 n < 10000 时 , 我 们 递 推 计 算 ; 否 则 我 们 直 接 套 公 式 计 算 。 由于本题误差在10^8数量级,故当n<10000时,我们递推计算;否则我们直接套公式计算。 由于本题误差在108数量级,故当n<10000时,我们递推计算;否则我们直接套公式计算。
法一代码:
#include法二代码:
#include本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!