一阶电路误差分析_自控原理分析曲轴一阶二阶震动

时域方法是最基本的方法，也是我们在分析时最先想到的方法，它可以直接提供系统时间响应内的所有内容，直观且明确，但是也有它的缺点，那就是这一方法必须要基于求解系统输出的解析法，过程很是繁琐，这一局限性也就决定了应用时域法进行分析的系统阶数不能太高。
接下来分别给出一阶系统和二阶系统典型结构和其性能指标的定义，对系统输入典型输入信号，研究对应响应的情况，在这其中，最重点的是二阶系统的阶跃响应，其余的响应仅作了解即可。注意到性能指标只能定量的描述一个系统响应的情况，考虑前面所提到的对于一个系统的基本要求：“稳、准、快”。其中“快”——动态性能；“稳”——基本要求；“准”——稳态要求，往后的内容都是围绕这三个字。对于“快”，其实就是系统的性能指标，对于“稳”，时域法介绍了赫尔维玆判据和劳斯判据，对于“准”，介绍了稳态误差还有校正方法。NO.1 一阶系统
我们从最简单的一阶系统说起，以下是一阶系统的典型结构：

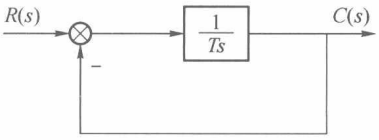
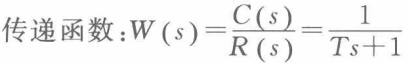
一阶系统中，只有特征参数：时间常数T。
虽然有五个典型输入信号，但一般我们只研究阶跃输入对应的响应，我们把阶跃信号称为“标准输入”，其单位阶跃响应曲线如下：

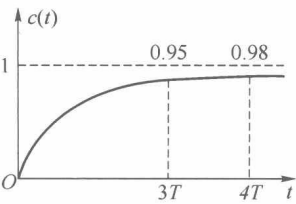
对于一阶系统，对应的性能指标有两个：上升时间

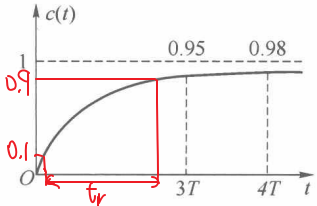
2.调节时间指第一次进入误差带且信号以后都不出误差带的时间。在响应曲线上表示为：

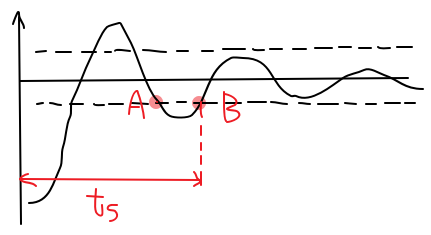
注意:如上图，调节时间不是到A点的时间，因为曲线在A点以后还有出了误差带的部分。而B点以后曲线再也不出误差带，所以调节时间应该为到B点的时间。因为一阶系统的响应是单调的，并没有振荡，所以在一阶系统中，并没有超调量的概念，因为响应曲线没有超出稳态值的部分。
在一阶系统求解对于五种输入信号时对应的响应时，虽然这部分只做了解，但这一求解过程中要求掌握一个重要的计算方法：留数定理。该种方法其实就是用来分解部分分式的，通式为：

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！