西电计科院大学物理二期末复习笔记下

大学物理二期末复习笔记下

博主是21级计科院的，大学物理二97分，这是期末复习期间整理的笔记（其二），基本全部涵盖期末考试重点范围，有需要的学弟学妹可以作为参考

第三章 电磁感应与电磁场

第一讲 电磁感应的基本规律

1.1 电动势

闭合回路上：
ξ = ∮ E k ⋅ d l (1) \xi = \oint\boldsymbol{E}_k\cdot d\boldsymbol{l}\tag{1} ξ=∮Ek​⋅dl(1)
对于一段电路$ab$：
ξ = ∫ a b E k ⋅ d l (2) \xi = \int_a^b\boldsymbol{E}_k\cdot d\boldsymbol{l}\tag{2} ξ=∫ab​Ek​⋅dl(2)
其中， E k \boldsymbol{E}_k Ek​表示非静电性电场强度；

1.2 法拉第电磁感应定律

ξ i = − d Φ d t (3) \xi_i=-\frac{d\Phi}{dt}\tag{3} ξi​=−dtdΦ​(3)
由楞次定律确定方向$\Rightarrow$方向相反；

1.3 多匝串联线圈

ξ i = − d d t ( ∑ k = 1 N Φ k ) = − d Ψ d t (4) \xi_i=-\frac{d}{dt}(\sum_{k=1}^N\Phi_k)=-\frac{d\Psi}{dt}\tag{4} ξi​=−dtd​(k=1∑N​Φk​)=−dtdΨ​(4)
ξ i = − d Ψ d t = − N d Φ d t ( Φ i = Φ j , 1 ≤ i , j ≤ N ) (5) \xi_i=-\frac{d\Psi}{dt}=-N\frac{d\Phi}{dt}(\Phi_i=\Phi_j, 1 \leq i,j \leq N)\tag{5} ξi​=−dtdΨ​=−NdtdΦ​(Φi​=Φj​,1≤i,j≤N)(5)
其中， Ψ = ∑ k = 1 N Φ k \Psi=\sum_{k=1}^N\Phi_k Ψ=∑k=1N​Φk​表示穿过各线圈的总磁通量，称为磁通链数；

1.4 长直螺线管

在长直螺线管外套一 $N$ 匝，总内阻为 $R$ 的圆线圈，$S$ 表示螺线管截面积：
B = μ 0 n I ⇒ Φ = B ⋅ S = μ 0 n I S 当通电电流均匀变化时，螺线管内的感应电动势 ξ i = − d Ψ d t = − N d Φ d t = − μ 0 n N S d I d t B=\mu_0nI\Rightarrow \Phi = \boldsymbol{B}\cdot\boldsymbol{S}=\mu_0nIS\\ 当通电电流均匀变化时，螺线管内的感应电动势\\ \xi_i=-\frac{d\Psi}{dt}=-N\frac{d\Phi}{dt}=-\mu_0nNS\frac{dI}{dt}\\ B=μ0​nI⇒Φ=B⋅S=μ0​nIS当通电电流均匀变化时，螺线管内的感应电动势ξi​=−dtdΨ​=−NdtdΦ​=−μ0​nNSdtdI​
【螺线管内磁感应强度】
感应电流  I i = ξ i R = − N R d Φ d t Δ q i = ∫ t 1 t 2 I i d t = − N R ∫ Φ 1 Φ 2 d Φ = − N R ( Φ 2 − Φ 1 ) ⟹ Φ 1 − Φ 2 = Δ q i R N 当 Φ 1 = 0 ∣ t = t 1 , Φ 2 = B S ∣ t = t 2 → + ∞ 时， ⇒ B = Δ q i R N S 感应电流\ I_i=\frac{\xi_i}{R}=-\frac{N}{R}\frac{d\Phi}{dt}\\ \Delta_{q_i}=\int_{t_1}^{t_2}I_idt=-\frac{N}{R}\int_{\Phi_1}^{\Phi_2}d\Phi=-\frac{N}{R}(\Phi_2-\Phi_1)\\ \Longrightarrow \Phi_1-\Phi_2=\frac{\Delta_{q_i}R}{N}\\ 当 \Phi_1=0\vert_{t=t_1},\Phi_2=BS\vert_{t=t_2\rightarrow+\infty} 时，\Rightarrow B=\frac{\Delta_{q_i}R}{NS} 感应电流 Ii​=Rξi​​=−RN​dtdΦ​Δqi​​=∫t1​t2​​Ii​dt=−RN​∫Φ1​Φ2​​dΦ=−RN​(Φ2​−Φ1​)⟹Φ1​−Φ2​=NΔqi​​R​当Φ1​=0∣t=t1​​,Φ2​=BS∣t=t2​→+∞​时，⇒B=NSΔqi​​R​

第二讲 动生电动势 感生电动势

2.1 动生电动势

导体棒 $ab$ 产生的动生电动势：
ξ i = ∫ a b E k ⋅ d l = ∫ a b ( v × B ) ⋅ d l (6) \xi_i=\int_a^b\boldsymbol{E}_k\cdot d\boldsymbol{l}=\int_a^b(\boldsymbol{v}\times\boldsymbol{B})\cdot d\boldsymbol{l}\tag{6} ξi​=∫ab​Ek​⋅dl=∫ab​(v×B)⋅dl(6)
闭合回路产生的动生电动势：
ξ i = ∮ L d ξ i = ∮ L ( v × B ) ⋅ d l (7) \xi_i=\oint_Ld\xi_i=\oint_L(\boldsymbol{v}\times\boldsymbol{B})\cdot d\boldsymbol{l}\tag{7} ξi​=∮L​dξi​=∮L​(v×B)⋅dl(7)
动生电动势方向由 $\mathbf{v}\times \mathbf{B}\cdot d\mathbf{l}$ 判定：
{ ξ i > 0 ⇒ u a < u b ξ i < 0 ⇒ u a > u b (8) \left\{\begin{array}{ccc}\xi_i>0\Rightarrow u_au_b\end{array}\right.\tag{8} {ξi​>0⇒ua​<ub​ξi​<0⇒ua​>ub​​(8)
注：积分路径：$a\to b$，在电源内部非静电性电场强度从负极指向正极， E k \boldsymbol{E}_k Ek​ 与积分方向一致时积分值为正，否则为负；

2.2 感生电动势

$感生电场假说\Rightarrow 有旋电场$

【回路固定不动】
ξ i = ∮ L E V ⋅ d l = − ∬ S ∂ B ∂ t ⋅ d S (9) \xi_i=\oint_L\boldsymbol{E}_V\cdot d\boldsymbol{l}=-\iint_S\frac{\partial \boldsymbol{B}}{\partial t}\cdot d\boldsymbol{S}\tag{9} ξi​=∮L​EV​⋅dl=−∬S​∂t∂B​⋅dS(9)
感生电动势方向由楞次定律判定；有旋电场度 E V E_V EV​ 的方向判定：闭合回路由右螺旋法则指向磁场方向选定回路绕行正方向，由式 $(9)$ 代入符号计算， E V E_V EV​ 正负与回路绕行方向保持一致；
当 E V E_V EV​ 相等，磁场均匀变化时，
ξ i = E V ∮ L d l = − ∂ B ∂ t ∬ S d S = − ∂ B ∂ t S ⟹ 计算某一闭合回路上的有旋电场强度 ( S 表示磁场面积 ) (10) \xi_i=E_V\oint_Ldl=-\frac{\partial{B}}{\partial{t}}\iint_SdS=-\frac{\partial{B}}{\partial{t}}S\tag{10}\\ \Longrightarrow\ 计算某一闭合回路上的有旋电场强度(\ S\ 表示磁场面积) ξi​=EV​∮L​dl=−∂t∂B​∬S​dS=−∂t∂B​S⟹ 计算某一闭合回路上的有旋电场强度( S 表示磁场面积)(10)

第三讲 自感与互感

3.1 自感电动势

Ψ = L I ⇒ ξ L = − d Ψ d t = − L d I d t ( L 为常量 ) (11) \Psi=LI\Rightarrow \xi_L=-\frac{d\Psi}{dt}=-L\frac{dI}{dt}\ \ (L为常量)\tag{11} Ψ=LI⇒ξL​=−dtdΨ​=−LdtdI​  (L为常量)(11)
式中 $L$ 表示自感系数，与 $I$ 无关(存在铁磁质时与 $I$ 有关)，仅有回路的匝数、几何形状、大小以及周围介质磁导率决定；

3.2 长直螺线管自感系数

【空心自感线圈】
B = μ 0 n I = μ 0 N l I ⇒ Ψ = N B S = μ 0 N 2 l π R 2 I ⟹ L = Ψ I = μ 0 N 2 π R 2 l = μ 0 n 2 V ( V = π R 2 l ) (12) B = \mu_0nI=\mu_0\frac{N}{l}I\Rightarrow \Psi=NBS=\mu_0\frac{N^2}{l}\pi R^2I\\ \Longrightarrow L=\frac{\Psi}{I}=\frac{\mu_0N^2\pi R^2}{l}=\mu_0n^2V\ (V=\pi R^2l)\tag{12} B=μ0​nI=μ0​lN​I⇒Ψ=NBS=μ0​lN2​πR2I⟹L=IΨ​=lμ0​N2πR2​=μ0​n2V (V=πR2l)(12)

3.3 传输线的分布电感

两长直平行导线电流 $I$，半径 r 0 r_0 r0​，轴线间距 $d$，且 r 0 ≤ d r_0\leq d r0​≤d；
导线微元 : d Φ 1 = B d S = μ 0 I 2 π r l d r ⇒ Φ 1 = ∫ r 0 d − r 0 μ 0 I l 2 π d r r = μ 0 I l 2 π ln ⁡ ( d − r 0 r 0 ) { Φ = Φ 1 + Φ 2 = 2 Φ 1 ( 电流反向 ) Φ = Φ 1 + Φ 2 = 0 ( 电流同向 ) L = Φ I = μ 0 π l ln ⁡ ( d − r 0 r 0 ) ≈ μ 0 π l ln ⁡ d r 0 ( 电流反向 ) (13) 导线微元:d\Phi_1=BdS=\frac{\mu_0I}{2\pi r}ldr\\ \Rightarrow \Phi_1=\int_{r_0}^{d-r_0}\frac{\mu_0Il}{2\pi}\frac{dr}{r}=\frac{\mu_0Il}{2\pi}\ln(\frac{d-r_0}{r_0})\\ \left\{\begin{array}{c}\Phi=\Phi_1+\Phi_2=2\Phi_1\ \ (电流反向)\\\Phi=\Phi_1+\Phi_2=0\ \ \ \ \ \ \ (电流同向)\end{array}\right.\\ L=\frac{\Phi}{I}=\frac{\mu_0}{\pi}l\ln(\frac{d-r_0}{r_0})\approx \frac{\mu_0}{\pi}l\ln\frac{d}{r_0}\ \ (电流反向)\tag{13} 导线微元:dΦ1​=BdS=2πrμ0​I​ldr⇒Φ1​=∫r0​d−r0​​2πμ0​Il​rdr​=2πμ0​Il​ln(r0​d−r0​​){Φ=Φ1​+Φ2​=2Φ1​  (电流反向)Φ=Φ1​+Φ2​=0       (电流同向)​L=IΦ​=πμ0​​lln(r0​d−r0​​)≈πμ0​​llnr0​d​  (电流反向)(13)

3.4 互感电动势

{ Ψ 21 = M 21 I 1 ( 回路 1 对回路 2 ) Ψ 12 = M 12 I 2 ( 回路 2 对回路 1 ) M 21 = M 12 = M ⟹ ξ M = − M d I d t (14) \left\{\begin{array}{c}\Psi_{21}=M_{21}I_1\ \ (回路1对回路2)\\\Psi_{12}=M_{12}I_2\ \ (回路2对回路1)\\M_{21}=M_{12}=M\end{array}\right.\\\Longrightarrow \xi_M=-M\frac{dI}{dt}\tag{14} ⎩ ⎨ ⎧​Ψ21​=M21​I1​  (回路1对回路2)Ψ12​=M12​I2​  (回路2对回路1)M21​=M12​=M​⟹ξM​=−MdtdI​(14)
式中 M 21 M_{21} M21​ 表示回路 $1$ 对回路 $2$ 的互感系数， M 12 M_{12} M12​ 表示回路 $2$ 对回路 $1$ 的互感系数；$M$ 表示两个回路间的互感系数，与 $I$ 无关(存在铁磁质时与 $I$ 有关)，由回路的匝数、几何形状、尺寸、周围介质磁导率以及回路的相对位置决定；

M 12 = M 21 = M ⇒ 转换研究对象简化计算互感系数 ⇒ 互感电动势 M_{12}=M_{21}=M\Rightarrow 转换研究对象简化计算互感系数\Rightarrow 互感电动势 M12​=M21​=M⇒转换研究对象简化计算互感系数⇒互感电动势

第四讲 磁能

4.1 自感磁能

{ d A = − ξ L i d t ξ L = − L d i d t ⇒ d A = L i d i ⟹ A = ∫ 0 I L i d i = 1 2 L I 2 (15) \left\{\begin{array}{c}dA=-\xi_Lidt\\\xi_L=-L\frac{di}{dt}\end{array}\right.\Rightarrow dA=Lidi\\ \Longrightarrow A=\int_0^ILidi=\frac{1}{2}LI^2\tag{15} {dA=−ξL​idtξL​=−Ldtdi​​⇒dA=Lidi⟹A=∫0I​Lidi=21​LI2(15)

$即\ \ \ \ \ W_m=\frac{1}{2}LI^2\ \ \ \ \ \ (自感磁能) $
当有磁场能量时可以利用  L = 2 W m I 2 计算自感系数 当有磁场能量时可以利用\ L=\frac{2W_m}{I^2}\ 计算自感系数 当有磁场能量时可以利用 L=I22Wm​​ 计算自感系数

式中，$L$ 表示线圈自感，$I$ 表示线圈所通电流；

4.2 长直螺线管磁能

由式 ( 12 ) ⇒ L = μ n 2 V ⇒ W m = 1 2 L I 2 = 1 2 μ n 2 I 2 V B = μ n I ⟹ H = B μ = n I (16) 由式(12)\Rightarrow L=\mu n^2V\Rightarrow W_m=\frac{1}{2}LI^2=\frac{1}{2}\mu n^2I^2V\\ B=\mu nI\Longrightarrow H=\frac{B}{\mu}=nI\tag{16} 由式(12)⇒L=μn2V⇒Wm​=21​LI2=21​μn2I2VB=μnI⟹H=μB​=nI(16)

W m = 1 2 B H V W_m=\frac{1}{2}BHV Wm​=21​BHV
磁能密度        ω m = W m V = 1 2 B H = 1 2 B 2 μ 0 μ r 磁能密度\ \ \ \ \ \ \ \omega_m=\frac{W_m}{V}=\frac{1}{2}BH=\frac{1}{2}\frac{B^2}{\mu_0\mu_r} 磁能密度       ωm​=VWm​​=21​BH=21​μ0​μr​B2​

4.3 有限体积内的磁能

W m = ∫ V d W m = 1 2 ∫ V B H d V (17) W_m=\int_VdW_m=\frac{1}{2}\int_VBHdV\tag{17} Wm​=∫V​dWm​=21​∫V​BHdV(17)

第五讲 麦克斯韦电磁场理论

5.1 位移电流

{ 传导电流 ⇐ 电荷定向移动形成的电流 位移电流 ⇐ 电位移通量的变化率 ( 变化的电场 ) Φ D = D S = ε E S = ε ⋅ σ ε S = σ S ⟹ d Φ d t = d d t ( σ S ) = d q d t = I ( 传导电流 ) (18) \left\{\begin{array}{c}传导电流\Leftarrow 电荷定向移动形成的电流\\位移电流\Leftarrow 电位移通量的变化率(变化的电场)\end{array}\right.\\ \Phi_D=DS=\varepsilon ES=\varepsilon\cdot\frac{\sigma}{\varepsilon}S=\sigma S\\ \Longrightarrow \frac{d\Phi}{dt}=\frac{d}{dt}(\sigma S)=\frac{dq}{dt}=I\ (传导电流)\tag{18} {传导电流⇐电荷定向移动形成的电流位移电流⇐电位移通量的变化率(变化的电场)​ΦD​=DS=εES=ε⋅εσ​S=σS⟹dtdΦ​=dtd​(σS)=dtdq​=I (传导电流)(18)

⟹ I D = d Φ D d t = d D d t S = ε d E d t S ( 位移电流 ) \Longrightarrow I_D = \frac{d\Phi_D}{dt}=\frac{dD}{dt}S=\varepsilon\frac{dE}{dt}S\ (位移电流) ⟹ID​=dtdΦD​​=dtdD​S=εdtdE​S (位移电流)
⟹ 全电流 = I + I D \Longrightarrow 全电流 = I+I_D ⟹全电流=I+ID​
非恒定电路中传导电流不连续但全电流保持连续

5.2 全电流安培环路定理

∮ L H ⋅ d l = I + I D I D = d Φ D d t = ∫ S d D d t ⋅ S (19) \oint_L\boldsymbol{H}\cdot d\boldsymbol{l}=I+I_D\\ I_D =\frac{d\Phi_D}{dt}= \int_S\frac{d\boldsymbol{D}}{dt}\cdot\boldsymbol{S}\tag{19} ∮L​H⋅dl=I+ID​ID​=dtdΦD​​=∫S​dtdD​⋅S(19)

5.3 麦克斯韦方程组

电场 E 、 D = { 自由电荷产生的静电场 E 1 、 D 1 变化磁场产生的有旋电场 E 2 、 D 2 ⇒ { E = E 1 + E 2 D = D 1 + D 2 磁场 B 、 H = { 传导电流产生的磁场 B 1 、 H 1 位移电流产生的磁场 B 2 、 H 2 ⇒ { B = B 1 + B 2 H = H 1 + H 2 (20) 电场\boldsymbol{E}、\boldsymbol{D}=\left\{\begin{array}{c}自由电荷产生的静电场\boldsymbol{E_1}、\boldsymbol{D_1}\\ 变化磁场产生的有旋电场\boldsymbol{E_2}、\boldsymbol{D_2}\end{array}\right.\Rightarrow \left\{\begin{array}{c}\boldsymbol{E}=\boldsymbol{E_1}+\boldsymbol{E_2}\\ \boldsymbol{D}=\boldsymbol{D_1}+\boldsymbol{D_2}\end{array}\right.\\ 磁场\boldsymbol{B}、\boldsymbol{H}=\left\{\begin{array}{c}传导电流产生的磁场\boldsymbol{B_1}、\boldsymbol{H_1}\\ 位移电流产生的磁场\boldsymbol{B_2}、\boldsymbol{H_2}\end{array}\right.\Rightarrow \left\{\begin{array}{c}\boldsymbol{B}=\boldsymbol{B_1}+\boldsymbol{B_2}\\ \boldsymbol{H}=\boldsymbol{H_1}+\boldsymbol{H_2}\end{array}\right.\tag{20} 电场E、D={自由电荷产生的静电场E1​、D1​变化磁场产生的有旋电场E2​、D2​​⇒{E=E1​+E2​D=D1​+D2​​磁场B、H={传导电流产生的磁场B1​、H1​位移电流产生的磁场B2​、H2​​⇒{B=B1​+B2​H=H1​+H2​​(20)

电场的高斯定理	∮ S D ⋅ d S = ∑ i q i \oint_S\boldsymbol{D}\cdot d\boldsymbol{S}=\sum_iq_i ∮S​D⋅dS=∑i​qi​	电场是有源场
法拉第电磁感应定律	∮ L E ⋅ d l = − ∬ S ∂ B ∂ t ⋅ d S \oint_L\boldsymbol{E}\cdot d\boldsymbol{l}=-\iint_S\frac{\partial{\boldsymbol{B}}}{\partial{t}}\cdot d\boldsymbol{S} ∮L​E⋅dl=−∬S​∂t∂B​⋅dS	静电场是保守(无旋、有势)场
磁场的高斯定理	∮ S B ⋅ d S = 0 \oint_S\boldsymbol{B}\cdot d\boldsymbol{S}=0 ∮S​B⋅dS=0	磁场是无源场
全电流安培环路定理	∮ L H ⋅ d l = ∑ ( I D + I ) \oint_L\boldsymbol{H}\cdot d\boldsymbol{l}=\sum(I_D+I) ∮L​H⋅dl=∑(ID​+I)	磁场是有旋(非保守)场

位移电流  I d 位移电流\ I_d 位移电流 Id​
Φ D = ∬ D ⋅ d S I d = d Φ D d t ⇒ 位移电流密度     j d = I d S \Phi_D = \iint\boldsymbol{D}\cdot d\boldsymbol{S}\\ I_d = \frac{d\Phi_D}{dt}\\ \Rightarrow 位移电流密度\ \ \ \ j_d = \frac{I_d}{S} ΦD​=∬D⋅dSId​=dtdΦD​​⇒位移电流密度    jd​=SId​​
$位移电流激发的磁场B$
∮ L H ⋅ d l = j d S \oint_L\boldsymbol{H}\cdot d\boldsymbol{l}=j_dS ∮L​H⋅dl=jd​S

第六讲 经典习题

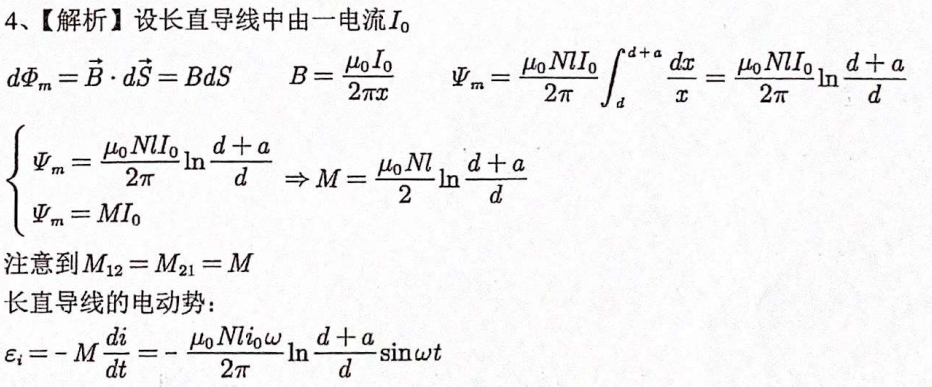
第四章 狭义相对论力学基础

第一讲 力学相对性原理

1.1 经典力学相对性原理

力学相对性原理	{ 对于描述力学现象的规律而言，所有惯性系都是等价的 力学规律的数学表达式应具有伽利略坐标变换的不变性 ( 协变性 ) \left\{\begin{array}{c}对于描述力学现象的规律而言，所有惯性系都是等价的\\力学规律的数学表达式应具有伽利略坐标变换的不变性(协变性)\end{array}\right. {对于描述力学现象的规律而言，所有惯性系都是等价的力学规律的数学表达式应具有伽利略坐标变换的不变性(协变性)​

1.2 伽利略坐标变化式

{ λ P S ′ + λ S ′ S = λ P S ⟹ λ ′ = λ − μ t ( λ = x , y , z , v , a , μ = u ) t ′ = t (1) \left\{\begin{array}{c}\lambda_{PS'}+\lambda_{S'S}=\lambda_{PS}\Longrightarrow \lambda' = \lambda-\mu t\ \ (\lambda=x,y,z,\boldsymbol{v},\boldsymbol{a},\mu=u)\\t'=t\end{array}\right.\tag{1} {λPS′​+λS′S​=λPS​⟹λ′=λ−μt  (λ=x,y,z,v,a,μ=u)t′=t​(1)

第二讲 狭义相对论基本假设

狭义相对论的相对性原理	{ 在所有惯性系中，一切物理学定理都相同，即具有相同的数学表达式 对于描述一切物理现象的规律而言，所有惯性系都是等价的 \left\{\begin{array}{c}在所有惯性系中，一切物理学定理都相同，即具有相同的数学表达式\\对于描述一切物理现象的规律而言，所有惯性系都是等价的\end{array}\right. {在所有惯性系中，一切物理学定理都相同，即具有相同的数学表达式对于描述一切物理现象的规律而言，所有惯性系都是等价的​
光速不变原理	$在所有惯性系中，真空中光沿各个方向传播的速率都等于同一个恒量c，与光源和观察者的运动状态无关$

第三讲 狭义相对论的时空观

3.1 同时性的相对性

{ 异地发生的两个同时事件，同时性具有相对性 ( 对任意参考系 ) 同地发生的两个同时事件，同时性具有绝对性 ( 对任意参考系 ) \left\{\begin{array}{c}异地发生的两个同时事件，同时性具有相对性(对任意参考系)\\ 同地发生的两个同时事件，同时性具有绝对性(对任意参考系)\end{array}\right. {异地发生的两个同时事件，同时性具有相对性(对任意参考系)同地发生的两个同时事件，同时性具有绝对性(对任意参考系)​

3.2 时间延缓

时间间隔具有相对性

τ = τ 0 1 − ( u c ) 2 = γ τ 0 (2) \tau=\frac{\tau_0}{\sqrt{1-(\frac{u}{c})^2}}=\gamma\tau_0\tag{2} τ=1−(cu​)2 ​τ0​​=γτ0​(2)
式中， γ = 1 1 − ( u c ) 2 \gamma = \frac{1}{\sqrt{1-(\frac{u}{c})^2}} γ=1−(cu​)2 ​1​， τ 0 \tau_0 τ0​ 表示同地不同时的两事件的时间间隔称为原时，且在不同参考系中测得的时间间隔以原时最短；

3.3 长度收缩

长度测量具有相对性

L ′ = L 1 − ( u c ) 2 (3) L'=L\sqrt{1-(\frac{u}{c})^2}\tag{3} L′=L1−(cu​)2 ​(3)
式中，$L$ 表示观测者静止时测得的长度(原长)， L ′ L' L′ 表示在沿尺长度方向运动速度为 $u$ 时测得的长度，且在不同参考系中测得的长度以原长最长；

第四讲 洛伦兹变换

4.1 时空坐标变换

P 在 S 中的时空坐标 ( x , y , z , t ) , 在 S ′ 中的时空坐标 ( x ′ , y ′ , z ′ , t ′ ) S 系中测得 S ′ 中坐标 x ′ ′ = x ′ 1 − ( u c ) 2 ( 长度收缩 ) ⟹ 在 S 系中 P 坐标 x = u t + x ′ ′ = u t + x ′ 1 − ( u c ) 2 S ′ 系中测得 S 中坐标 x 1 = x 1 − ( u c ) 2 ( 长度收缩 ) ⟹ 在 S ′ 系中 P 坐标 x ′ = x 1 − u t ′ = x 1 − ( u c ) 2 − u t ′ ⟹ x ′ = x − u t 1 − ( u c ) 2 , t ′ = t − u c 2 x 1 − ( u c ) 2 (4) P在S中的时空坐标(x,y,z,t),在S'中的时空坐标(x',y',z',t')\\ S系中测得S'中坐标x''= x'\sqrt{1-(\frac{u}{c})^2}\ \ \ (长度收缩)\\ \Longrightarrow 在S系中P坐标 x = ut + x''=ut+x'\sqrt{1-(\frac{u}{c})^2}\\ S'系中测得S中坐标x_1= x\sqrt{1-(\frac{u}{c})^2}\ \ \ (长度收缩)\\ \Longrightarrow 在S'系中P坐标 x' = x_1 -ut' = x\sqrt{1-(\frac{u}{c})^2} - ut'\\ \Longrightarrow x' = \frac{x-ut}{\sqrt{1-(\frac{u}{c})^2}},t' = \frac{t-\frac{u}{c^2}x}{\sqrt{1-(\frac{u}{c})^2}}\tag{4} P在S中的时空坐标(x,y,z,t),在S′中的时空坐标(x′,y′,z′,t′)S系中测得S′中坐标x′′=x′1−(cu​)2 ​   (长度收缩)⟹在S系中P坐标x=ut+x′′=ut+x′1−(cu​)2 ​S′系中测得S中坐标x1​=x1−(cu​)2 ​   (长度收缩)⟹在S′系中P坐标x′=x1​−ut′=x1−(cu​)2 ​−ut′⟹x′=1−(cu​)2 ​x−ut​,t′=1−(cu​)2 ​t−c2u​x​(4)
式中，$u$ 表示 S ′ S' S′ 相对于 $S$ 的速度(相对速度)， x ′ x' x′ 表示待求坐标系中参量；
推导时间变换式
由 x ′ = x − u t 1 − ( u c ) 2 及逆变换 x = x ′ + u t ′ 1 − ( u c ) 2 联立消去 x ′ 解 t ′ 由x' = \frac{x-ut}{\sqrt{1-(\frac{u}{c})^2}}及逆变换x = \frac{x'+ut'}{\sqrt{1-(\frac{u}{c})^2}}联立消去x'解t' 由x′=1−(cu​)2 ​x−ut​及逆变换x=1−(cu​)2 ​x′+ut′​联立消去x′解t′

4.2 时空间隔变换

P 1 , P 2 在 S 中的时空坐标 ( x 1 , y 1 , z 1 , t 1 ) , ( x 2 , y 2 , z 2 , t 2 ) , 在 S ′ 中的时空坐标 ( x 1 ′ , y 1 ′ , z 1 ′ , t 1 ′ ) , ( x 2 ′ , y 2 ′ , z 2 ′ , t 2 ′ ) 由 S → S ′ Δ t ′ = Δ t − u c 2 Δ x 1 − β 2 , Δ x ′ = Δ x − u Δ t 1 − β 2 ( β = u c ) 由 S ′ → S Δ t = Δ t ′ + u c 2 Δ x ′ 1 − β 2 , Δ x = Δ x ′ + u Δ t ′ 1 − β 2 ( β = u c ) (5) P_1,P_2在S中的时空坐标(x_1,y_1,z_1,t_1),(x_2,y_2,z_2,t_2),在S'中的时空坐标(x_1',y_1',z_1',t_1'),(x_2',y_2',z_2',t_2')\\ 由S\rightarrow S'\\ \Delta t'=\frac{\Delta t-\frac{u}{c^2}\Delta x}{\sqrt{1-\beta^2}},\Delta x'=\frac{\Delta x-u\Delta t}{\sqrt{1-\beta^2}}\ (\beta = \frac{u}{c})\\ 由S'\rightarrow S\\ \Delta t=\frac{\Delta t'+\frac{u}{c^2}\Delta x'}{\sqrt{1-\beta^2}},\Delta x=\frac{\Delta x'+u\Delta t'}{\sqrt{1-\beta^2}}\ (\beta = \frac{u}{c})\tag{5} P1​,P2​在S中的时空坐标(x1​,y1​,z1​,t1​),(x2​,y2​,z2​,t2​),在S′中的时空坐标(x1′​,y1′​,z1′​,t1′​),(x2′​,y2′​,z2′​,t2′​)由S→S′Δt′=1−β2 ​Δt−c2u​Δx​,Δx′=1−β2 ​Δx−uΔt​ (β=cu​)由S′→SΔt=1−β2 ​Δt′+c2u​Δx′​,Δx=1−β2 ​Δx′+uΔt′​ (β=cu​)(5)
式中，$u$ 关联于坐标轴选取的正方向，一般选定 $S$ 系运动方向为坐标轴正方向；

4.3 爱因斯坦速度相加定律

由式 ( 4 ) 求微分 ⇒ { d x ′ = ( v x − u ) 1 − β 2 d t d y ′ = d y d z ′ = d z d t ′ = ( 1 − u c 2 v x ) 1 − β 2 d t ⇒ v x ′ = d x ′ d t ′ = v x − u 1 − u c 2 v x ⇒ v y ′ = d y ′ d t ′ = v y 1 − β 2 1 − u c 2 v x ⇒ v z ′ = d z ′ d t ′ = v z 1 − β 2 1 − u c 2 v x (6) 由式(4)求微分\Rightarrow\left\{\begin{array}{c}dx'=\frac{(v_x-u)}{\sqrt{1-\beta^2}}dt\\dy'= dy\\dz'= dz\\dt' = \frac{(1-\frac{u}{c^2}v_x)}{\sqrt{1-\beta^2}}dt\end{array}\right.\\ \Rightarrow v_x'=\frac{dx'}{dt'}=\frac{v_x-u}{1-\frac{u}{c^2}v_x}\\ \Rightarrow v_y'=\frac{dy'}{dt'}=\frac{v_y\sqrt{1-\beta^2}}{1-\frac{u}{c^2}v_x}\\ \Rightarrow v_z'=\frac{dz'}{dt'}=\frac{v_z\sqrt{1-\beta^2}}{1-\frac{u}{c^2}v_x}\tag{6} 由式(4)求微分⇒⎩ ⎨ ⎧​dx′=1−β2 ​(vx​−u)​dtdy′=dydz′=dzdt′=1−β2 ​(1−c2u​vx​)​dt​⇒vx′​=dt′dx′​=1−c2u​vx​vx​−u​⇒vy′​=dt′dy′​=1−c2u​vx​vy​1−β2 ​​⇒vz′​=dt′dz′​=1−c2u​vx​vz​1−β2 ​​(6)

第五讲 狭义相对论质点动力学

5.1 相对论动量和质量

m ( v ) = m 0 1 − ( u c ) 2 ( 质速关系式 ) ⟹ p = m v = m 0 1 − ( u c ) 2 v ⟹ F = d p d t = d d t ( m 0 1 − ( u c ) 2 v ) (7) m(v) = \frac{m_0}{\sqrt{1-(\frac{u}{c})^2}}\ (质速关系式)\\ \Longrightarrow \boldsymbol{p}=m\boldsymbol{v}=\frac{m_0}{\sqrt{1-(\frac{u}{c})^2}}\boldsymbol{v}\\ \Longrightarrow \boldsymbol{F}=\frac{d\boldsymbol{p}}{dt}=\frac{d}{dt}(\frac{m_0}{\sqrt{1-(\frac{u}{c})^2}}\boldsymbol{v})\tag{7} m(v)=1−(cu​)2 ​m0​​ (质速关系式)⟹p=mv=1−(cu​)2 ​m0​​v⟹F=dtdp​=dtd​(1−(cu​)2 ​m0​​v)(7)
式中， m 0 m_0 m0​ 表示物体静止质量；

5.2 相对论动能

E k = ∫ F ⋅ d r = ∫ d ( m v ) d t ⋅ d r = ∫ d ( m v ) ⋅ d r d t = ∫ d ( m v ) ⋅ v m ∝ v ⟹ d ( m v ) ⋅ v = ( v d m + m d v ) ⋅ v = v 2 d m + m v d v 式 ( 7 ) ⇒ m 2 v 2 = m 2 c 2 − m 0 2 c 2 ⇒ v 2 d m + m v d v = c 2 d m E k = ∫ m 0 m c 2 d m = m c 2 − m 0 c 2 (8) E_k = \int \boldsymbol{F}\cdot d\boldsymbol{r}=\int \frac{d(m\boldsymbol{v})}{dt}\cdot d\boldsymbol{r}=\int d(m\boldsymbol{v})\cdot \frac{d\boldsymbol{r}}{dt}=\int d(m\boldsymbol{v})\cdot\boldsymbol{v}\\ m\propto\boldsymbol{v}\Longrightarrow d(m\boldsymbol{v})\cdot\boldsymbol{v}=(\boldsymbol{v}dm+md\boldsymbol{v})\cdot \boldsymbol{v}=v^2dm+mvdv\\ 式(7)\Rightarrow m^2v^2=m^2c^2-m_0^2c^2\Rightarrow v^2dm+mvdv=c^2dm\\ E_k=\int_{m_0}^mc^2dm=mc^2-m_0c^2\tag{8} Ek​=∫F⋅dr=∫dtd(mv)​⋅dr=∫d(mv)⋅dtdr​=∫d(mv)⋅vm∝v⟹d(mv)⋅v=(vdm+mdv)⋅v=v2dm+mvdv式(7)⇒m2v2=m2c2−m02​c2⇒v2dm+mvdv=c2dmEk​=∫m0​m​c2dm=mc2−m0​c2(8)

5.3 质能方程

{ E = m c 2 ( 运动能量 ) E 0 = m 0 c 2 ( 静止能量 ) (9) \left\{\begin{array}{c}E=mc^2\ \ (运动能量)\\ E_0=m_0c^2\ \ (静止能量)\end{array}\right.\tag{9} {E=mc2  (运动能量)E0​=m0​c2  (静止能量)​(9)

5.4 光子质量

光子能量 E = h ν ( 爱因斯坦光子假说 ) ⟹ m φ = E c 2 = h ν c 2 = h c λ (10) 光子能量 E= h\nu\ \ (爱因斯坦光子假说)\\ \Longrightarrow m_\varphi=\frac{E}{c^2}=\frac{h\nu}{c^2}=\frac{h}{c\lambda}\tag{10} 光子能量E=hν  (爱因斯坦光子假说)⟹mφ​=c2E​=c2hν​=cλh​(10)

光子、中微子在真空中速率为 $c$，不可能静止因此静止能量等于零

5.5 相对论能量与动量关系

式 ( 7 ) ⇒ m 2 ( 1 − v 2 c 2 ) = m 0 2 ⟹ m 2 c 4 = m 2 v 2 c 2 + m 0 2 c 4 p = m v ⇒ E 2 = p 2 c 2 + E 0 2 光子   m 0 = 0 ⇒ E 0 = 0 ⇒ E 2 = p 2 c 2 ⟹ p = h ν c = h λ (11) 式(7)\Rightarrow m^2(1-\frac{v^2}{c^2})=m_0^2\\ \Longrightarrow m^2c^4=m^2v^2c^2+m_0^2c^4\\ p=mv\Rightarrow E^2=p^2c^2+E_0^2\\ 光子\ \ m_0=0\Rightarrow E_0=0\Rightarrow E^2=p^2c^2\\ \Longrightarrow p=\frac{h\nu}{c}=\frac{h}{\lambda}\tag{11} 式(7)⇒m2(1−c2v2​)=m02​⟹m2c4=m2v2c2+m02​c4p=mv⇒E2=p2c2+E02​光子  m0​=0⇒E0​=0⇒E2=p2c2⟹p=chν​=λh​(11)

第五章 量子物理基础

第一讲 普朗克量子假设

1.1 基本概念

热辐射	物体由其温度所决定的电磁辐射(温度越高，单位时间内辐射的能量越高)
平衡热辐射	当辐射和吸收达到平衡时，物体的温度不再发生变化而处于热平衡状态时的热辐射
单色辐射出射度(单色辐出度)	物体单位表面积在单位时间内发射的，波长在 $\lambda \to \lambda +d\lambda$ 范围内的辐射能 d M λ dM_\lambda dMλ​与波长间隔 $d\lambda$ 的比值
绝对黑体(黑体)	能够全部吸收各种波长的辐射能而不发生发射和透射的物体

1.2 单色辐出度

M λ ( T ) = d M λ d λ (1) M_\lambda(T)=\frac{dM_\lambda}{d\lambda}\tag{1} Mλ​(T)=dλdMλ​​(1)
【单色辐出度图】

温度越高	单色辐出度越大，峰值波长越短

1.3 普朗克量子假设

$$\epsilon =nh\nu \text{\hspace{1em}(2)}$$
式中，$\epsilon$ 表示腔壁中带电谐振子离散变化的能量，振子的频率为 $\nu$，$n$ 表示量子数，$h\nu$ 表示能量子——谐振子能量的最小单位(不是物质而是能量单位)；

第二讲 爱因斯坦光子理论

2.1 光电效应

金属及其化合物在光的照射下发射电子的现象

【光电效应伏安特性曲线】

照射光光强越大，饱和光电流越大
光电子最大初动能与照射光强度无关，而与频率成线性关系

2.2 光电效应方程

1 2 m v m 2 = e U a ( 遏止电压 ) h ν = A + 1 2 m v m 2 ( 光电效应方程 ) ν 0 = A h ( 截止频率 ) ⟹ U a = h e ν − A e (3) \frac{1}{2}mv_m^2=eU_a\ (遏止电压)\\ h\nu = A + \frac{1}{2}mv_m^2\ \ (光电效应方程)\\ \nu_0=\frac{A}{h}\ (截止频率)\\ \Longrightarrow U_a = \frac{h}{e}\nu-\frac{A}{e}\tag{3} 21​mvm2​=eUa​ (遏止电压)hν=A+21​mvm2​  (光电效应方程)ν0​=hA​ (截止频率)⟹Ua​=eh​ν−eA​(3)

第三讲 康普顿效应及光子理论解释

3.1 康普顿效应

单色 $X$ 射线被物质散射时，散射光两种波长中有一种波长比入射线长的散射现象

3.2 光子理论解释

【微观机制】——等价于微观粒子的弹性碰撞
入射光子频率 ν 0 , 散射角为 θ 的光子频率为 ν , 电子沿着与入射线成 φ 角的方向运动 , 静质量 m 0 , 动质量 m 动量守恒定律     { h ν 0 c = h ν c cos ⁡ θ + m v cos ⁡ φ h ν c sin ⁡ θ = m v sin ⁡ φ ⟹ m 2 v 2 c 2 = h 2 ( ν 0 2 − ν 2 − 2 ν 0 ν cos ⁡ θ ) (4) 入射光子频率\nu_0,散射角为\theta的光子频率为\nu,电子沿着与入射线成\varphi角的方向运动,静质量m_0,动质量m\\ 动量守恒定律\ \ \ \ \left\{\begin{array}{c}\frac{h\nu_0}{c}=\frac{h\nu}{c}\cos\theta+mv\cos\varphi\\ \frac{h\nu}{c}\sin\theta=mv\sin\varphi\end{array}\right.\\ \Longrightarrow m^2v^2c^2=h^2(\nu_0^2-\nu^2-2\nu_0\nu\cos\theta)\tag{4} 入射光子频率ν0​,散射角为θ的光子频率为ν,电子沿着与入射线成φ角的方向运动,静质量m0​,动质量m动量守恒定律    {chν0​​=chν​cosθ+mvcosφchν​sinθ=mvsinφ​⟹m2v2c2=h2(ν02​−ν2−2ν0​νcosθ)(4)
能量守恒定律            h v 0 + m 0 c 2 = h v + m c 2 { 式 ( 5 ) 平方 − 式 ( 4 ) m 2 ( 1 − v 2 c 2 ) = m 0 2 ⟹ m 0 c 2 ( ν 0 − ν ) = h ν 0 ν ( 1 − cos ⁡ θ ) (5) 能量守恒定律\ \ \ \ \ \ \ \ \ \ \ hv_0+m_0c^2=hv+mc^2\tag{5}\\ \left\{\begin{array}{c}式(5)平方-式(4)\\m^2(1-\frac{v^2}{c^2})=m_0^2\end{array}\right.\Longrightarrow m_0c^2(\nu_0-\nu)=h\nu_0\nu(1-\cos\theta) 能量守恒定律           hv0​+m0​c2=hv+mc2{式(5)平方−式(4)m2(1−c2v2​)=m02​​⟹m0​c2(ν0​−ν)=hν0​ν(1−cosθ)(5)
⟹ Δ λ = λ − λ 0 = c ν − c ν 0 = h m 0 c ( 1 − cos ⁡ θ ) > 0 = 2 h m 0 c sin ⁡ 2 θ 2 = 2 λ C sin ⁡ 2 θ 2 (6) \Longrightarrow \Delta\lambda = \lambda - \lambda_0=\frac{c}{\nu}-\frac{c}{\nu_0}=\frac{h}{m_0c}(1-\cos\theta)>0\\ =\frac{2h}{m_0c}\sin^2\frac{\theta}{2}=2\lambda_C\sin^2\frac{\theta}{2}\tag{6} ⟹Δλ=λ−λ0​=νc​−ν0​c​=m0​ch​(1−cosθ)>0=m0​c2h​sin22θ​=2λC​sin22θ​(6)
式中， λ C = h m 0 c \lambda_C=\frac{h}{m_0c} λC​=m0​ch​ 称为电子的康普顿波长；

第四讲 氢原子光谱 玻尔氢原子理论

4.1 氢原子光谱实验规律

$氢原子光谱——线状光谱$
【里德伯 − 里兹合并原则】光谱线波数  ν ~ = 1 λ = T ( k ) − T ( n ) = R H ( 1 k 2 − 1 n 2 ) ( k 、 n ∈ Z 且  n > k ) 【里德伯-里兹合并原则】光谱线波数\ \widetilde{\nu}=\frac{1}{\lambda}=T(k)-T(n)=R_H(\frac{1}{k^2}-\frac{1}{n^2})\ \ (k、n\in Z\ 且\ n>k) 【里德伯−里兹合并原则】光谱线波数 ν =λ1​=T(k)−T(n)=RH​(k21​−n21​)  (k、n∈Z 且 n>k)
$k=1(n=2,3,4,\cdots )——赖曼系k=2(n=3,4,5,\cdots )——巴耳末系$

4.2 玻尔氢原子理论——氢原子或类氢原子

【辐射频率公式】——辐射或吸收一个频率为 ν k n \nu_{kn} νkn​ 的光子
ν k n = ∣ E k − E n ∣ h (7) \nu_{kn} = \frac{|E_k-E_n|}{h}\tag{7} νkn​=h∣Ek​−En​∣​(7)
【角动量量子化条件】——轨道角动量不能连续变化
L = m v r = n h 2 π = n h ‾ , n = 1 , 2 , 3 , ⋯ (8) L=mvr=n\frac{h}{2\pi}=n\overline{h},\ \ n = 1,2,3,\cdots\tag{8} L=mvr=n2πh​=nh,  n=1,2,3,⋯(8)
式中， h ‾ = h 2 π \overline{h}=\frac{h}{2\pi} h=2πh​ 表示约化普朗克常数；
【电子轨道半径】——电子轨道半径不能连续变化
m v 2 r = 1 4 π ε 0 e 2 r 2 又由式 ( 8 ) ⇒ r n = n 2 ( ε 0 h 2 π m e 2 ) = n 2 r 1 ( n = 1 , 2 , 3 , ⋯ ) (9) m\frac{v^2}{r}=\frac{1}{4\pi\varepsilon_0}\frac{e^2}{r^2}\\ 又由式(8)\Rightarrow r_n=n^2(\frac{\varepsilon_0h^2}{\pi me^2})=n^2r_1\ (n=1,2,3,\cdots)\tag{9} mrv2​=4πε0​1​r2e2​又由式(8)⇒rn​=n2(πme2ε0​h2​)=n2r1​ (n=1,2,3,⋯)(9)
式中 r 1 r_1 r1​ 表示氢原子中电子的最小轨道半径，称为玻尔半径；

$n=1的定态——基态n=2,3,4,\cdots 各态——受激态$

$氢原子能量=电子动能+电子电势能$

量子数为 $n$ 的定态时氢原子能量：
E = 1 2 m v 2 − 1 4 π ε 0 e 2 r = − 1 8 π ε 0 e 2 r ⟹ E n = − 1 8 π ε 0 e 2 r n = − 1 n 2 ( m e 4 8 ε 0 2 h 2 ) ( n = 1 , 2 , 3 , ⋯ ) (10) E=\frac{1}{2}mv^2-\frac{1}{4\pi\varepsilon_0}\frac{e^2}{r}=-\frac{1}{8\pi\varepsilon_0}\frac{e^2}{r}\\ \Longrightarrow E_n=-\frac{1}{8\pi\varepsilon_0}\frac{e^2}{r_n}=-\frac{1}{n^2}(\frac{me^4}{8\varepsilon_0^2h^2})\ \ \ (n=1,2,3,\cdots)\tag{10} E=21​mv2−4πε0​1​re2​=−8πε0​1​re2​⟹En​=−8πε0​1​rn​e2​=−n21​(8ε02​h2me4​)   (n=1,2,3,⋯)(10)
当  n → ∞ 时 , r n → ∞ , E n → 0 , 能级趋于连续 , 原子趋于电离 E > 0 时 , 原子处于电离状态 , 能量可连续变化 ⇓ { 电离能 : 使原子或分子电离所需要的能量 原子电离电势 : 电子使原子刚好电离所需的加速电势差 当\ n\rightarrow \infty\ 时,\ r_n\rightarrow \infty,\ E_n\rightarrow0,\ 能级趋于连续,\ 原子趋于电离\\ E>0\ 时,\ 原子处于电离状态,\ 能量可连续变化\\ \Downarrow\\ \left\{\begin{array}{c}电离能: 使原子或分子电离所需要的能量\\ 原子电离电势:电子使原子刚好电离所需的加速电势差\end{array}\right. 当 n→∞ 时, rn​→∞, En​→0, 能级趋于连续, 原子趋于电离E>0 时, 原子处于电离状态, 能量可连续变化⇓{电离能:使原子或分子电离所需要的能量原子电离电势:电子使原子刚好电离所需的加速电势差​
【氢原子跃迁】
高能态跃迁到低能态发射一个光子其频率和波数：
ν n k = E n − E k h ( n > k ) ν ~ n k = 1 λ n k = ν n k c = 1 h c ( E n − E k ) (11) \nu_{nk}=\frac{E_n-E_k}{h}\ \ \ (n>k)\\ \widetilde{\nu}_{nk}=\frac{1}{\lambda_{nk}}=\frac{\nu_{nk}}{c}=\frac{1}{hc}(E_n-E_k)\tag{11} νnk​=hEn​−Ek​​   (n>k)ν nk​=λnk​1​=cνnk​​=hc1​(En​−Ek​)(11)

常用物理常数

物理常数	物理符号	取值
普朗克常数	$h$	6.62607015 × 1 0 − 34 J ⋅ s 6.62607015\times 10^{-34} \ \ J\cdot s 6.62607015×10−34  J⋅s
电子电量	$e$	1.6 × 1 0 − 19 C 1.6\times 10^{-19}\ \ C 1.6×10−19  C
光速	$c$	3 × 1 0 8 m / s 3\times 10^8\ \ m/s 3×108  m/s
真空电容率/真空介电常量	ε 0 \varepsilon_0 ε0​	8.85 × 1 0 − 12 C 2 ⋅ N − 1 ⋅ m − 2 8.85\times 10^{-12}\ \ C^2\cdot N^{-1}\cdot m^{-2} 8.85×10−12  C2⋅N−1⋅m−2

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！