790. 多米诺和托米诺平铺-动态规划算法优化

有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 “L” 的托米诺形。两种形状都可以旋转。

给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。

平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。

示例 1:

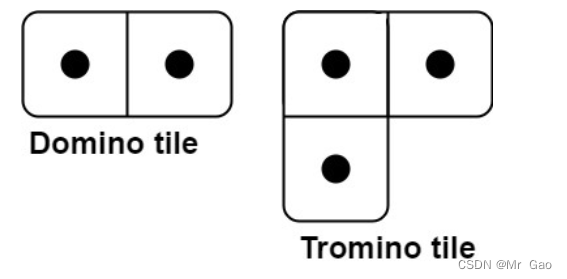
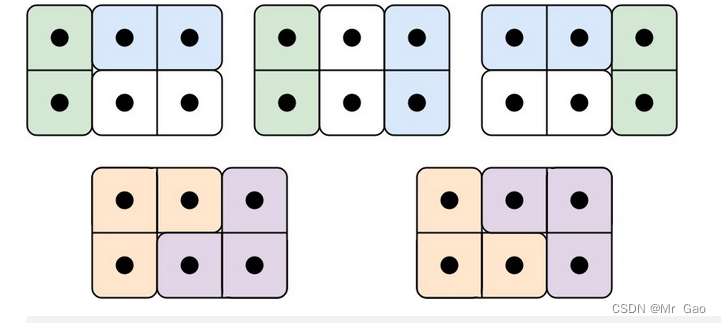
输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。

示例 2:

输入: n = 1
输出: 1

博主这个题目应该比很多动态规划的算法更好理解，我这个算法是更加优越的且更加易懂的，感兴趣的话，可以了解一下代码中的算法思想，解题代码如下：

const long long mod = 1e9 + 7;int numTilings(int n) {long long dp[n + 1][3];dp[0][0]=1;dp[1][0]=1;dp[1][1]=0;dp[1][2]=0;for(int i=2;i<=n;i++){dp[i][0]=(dp[i-1][0]+dp[i-1][1]+dp[i-1][2]+dp[i-2][0])% mod;dp[i][1]=(dp[i-2][0]+dp[i-1][2])%mod;dp[i][2]=(dp[i-2][0]+dp[i-1][1])%mod;}return dp[n][0]% mod;}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！