Matlab—计算圆周率近似值的4种方法

Matlab—计算圆周率近似值的4种方法

1.莱布尼茨公式

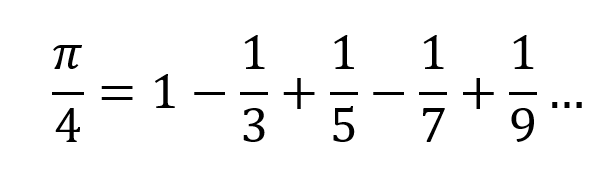
下面展示 代码——莱布尼茨公式

function s=count_pi(n)
s=0;
for n=1:n  s=s+(-1)^(n-1)/(2*n-1);
endpi=4*s;fprintf('π的近似值为%.6f ',pi)

2.欧拉公式

2.1 欧拉公式①

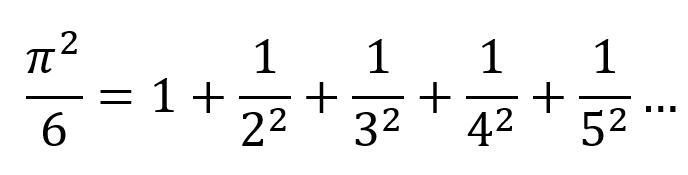
下面展示 代码——欧拉公式①

function s=count_pi(n)
s=0;
for n=1:n  s=s+1/n^2;
endpi=sqrt(6*s);fprintf('π的近似值为%.6f ',pi)

2.2 欧拉公式②

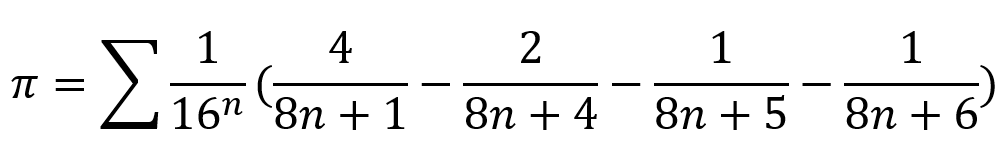
下面展示 代码——欧拉公式②

function s=count_pi(n)
s=0;
for n=0:n s=s+(1/16^n)*(4/(8*n+1)-2/(8*n+4)-1/(8*n+5)-1/(8*n+6));
endpi=s;fprintf('π的近似值为%.6f ',pi)

3.拉马努金公式

3.1 拉马努金公式①

下面展示 代码——拉马努金公式①

function s=count_pi(n)
s=0;
for n=0:n  s=((factorial(4*n)*(1103+26390*n))/((factorial(n))^4*396^(4*n)))+s;
ends=(2*sqrt(2)/9801)*s;pi=1/s;fprintf('π的近似值为%.6f ',pi)

3.2 拉马努金公式②

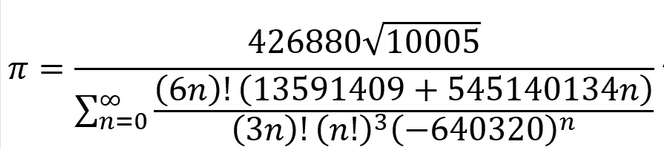
下面展示 代码——拉马努金公式②

function s=count_pi(n)
s=0;
for n=0:n  s=s+factorial(6*n)*(13591409+545140134*n)/(factorial(3*n)*(factorial(n))^3*(-640320)^(3*n));
enda=426880*sqrt(10005)/s;pi=a;fprintf('π的近似值为%.6f ',pi)

4.蒙特卡洛方法

4.1 蒙特卡洛方法①

下面展示 代码——蒙特卡洛方法①

function s=count_pi(n)
s=0;
n=10^n;
for n=1:n;x=rand(1);y=rand(1);if x^2+y^2<=1s=s+1;endend

4.2 蒙特卡洛方法②

下面展示 代码——蒙特卡洛方法②

function s=count_pi(n)
s=0;
for n=1:n  s=s+(-1)^(n-1)/(2*n-1);
endpi=4*s;fprintf('π的近似值为%.6f ',pi)

5.代码集合

下面展示 代码集合

function s=count_pi(n,flag)
%Mtalab计算Π的7种方法
%flag=1,2,3时，n取值尽可能大，数值越大，精确度越高
%flag=4时，n取值不宜超过40，否则输出结果为无效数值NaN
%flag=5时，n取值不宜超过27，否则输出结果为无效数值NaN
%flag=6,7时，n由于采用蒙特卡洛方法，误差是概率误差，所以只能得出一个近似值Π
%每次end之后，pi的赋值仅为个人习惯%% Method 1 莱布尼茨公式
if flag==1s=0;
for n=1:n  s=s+(-1)^(n-1)/(2*n-1);
endpi=4*s;fprintf('π的近似值为%.6f ',pi)%% Method 2 欧拉公式①
elseif flag==2s=0;for n=1:n  s=s+1/n^2;endpi=sqrt(6*s);fprintf('π的近似值为%.6f ',pi)%% Method 3 欧拉公式②
elseif flag==3s=0;for n=0:n s=s+(1/16^n)*(4/(8*n+1)-2/(8*n+4)-1/(8*n+5)-1/(8*n+6));endpi=s;fprintf('π的近似值为%.6f ',pi)%% Method 4 拉马努金公式①
elseif flag==4s=0;for n=0:n  s=((factorial(4*n)*(1103+26390*n))/((factorial(n))^4*396^(4*n)))+s;ends=(2*sqrt(2)/9801)*s;pi=1/s;fprintf('π的近似值为%.6f ',pi)%% Method 5 拉马努金公式②
elseif flag==5s=0;for n=0:n  s=s+factorial(6*n)*(13591409+545140134*n)/(factorial(3*n)*(factorial(n))^3*(-640320)^(3*n));enda=426880*sqrt(10005)/s;pi=a;fprintf('π的近似值为%.6f ',pi)%% Method 6 蒙特卡洛方法①
elseif flag==6s=0;n=10^n;for n=1:nx=rand(1);y=rand(1);if x^2+y^2 <= 1s=s+1;end
endpi=s/n*4;fprintf('π的近似值为%.6f ',pi)%% Method 7 蒙特卡洛方法②
elseif flag==7z=rand(n,2);a=z(:,1).^2+z(:,2).^2;b=(a<=1);m=sum(b);y=4*m/n;pi=y;fprintf('π的近似值为%.6f ',pi)end

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！