[HNOI2004]敲砖块

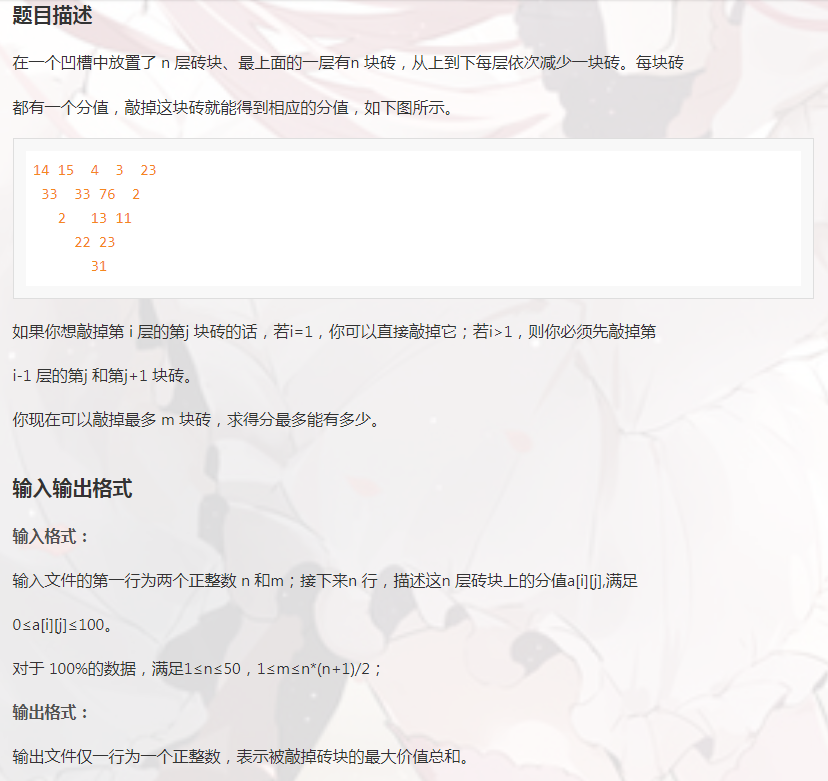
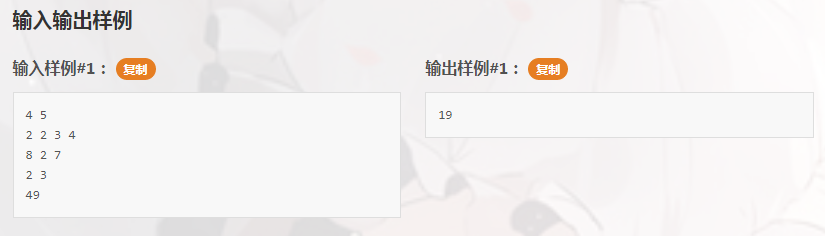
 直接用题目中三角形

我们发现无论是从上到下还是从下到上DP都会有后效性

这时我们发现第i列的情况只和第i+1列有关

于是我们产生了从右向左DP的思路

到这为止我的想法，就开始与别人不同了

我用f[i][j][k]表示，敲掉第i行第j列的那个块，和之前的k-1个块所能得到的最大分数

用ji[j][[k]表示，当前列的前一列j-n列敲掉k个块所能得到的最大分数

用滚动数组变为ji[k]方便书写

转移的话就拿f[j][i][k]=max(ji[k-j]+s[j][i],f[j][i][k]);来转移

但注意要特殊处理j=0的情况

for(int k=0;k<=m;k++) f[0][i][k]=ji[k];

总的来说此题细节极多，较好的DP题

实现如下：

#include 
#include 
#include 
#include 
#include 

转载于:https://www.cnblogs.com/cold-cold/p/10166498.html

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！