走进AC自动机
走进AC自动机
AC自动机,听这名字就很高大上的亚子,起初还以为就是“AC自动机”。。。。。。开始真正的走进AC自动机了
简单介绍:
AC自动机即为:多模匹配问题(像:经典的KMP算法就是单一模式匹配),于是要学会AC自动机,我们必须知道什么是Trie,也就是字典树。Trie树,又称单词查找树或键树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计和排序大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。
于是就了解字典树是个啥东西
字典树
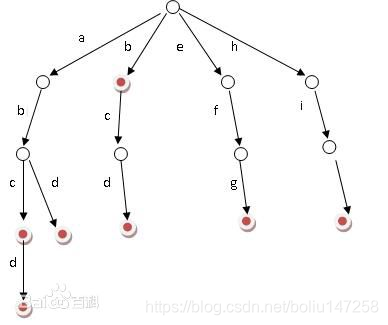
看图秒懂,有树的基本知识,就能明白字典树是个什么东东了
基本性质:
1、根节点不包含字符,除根节点外每一个节点都只包含一个字符;
2、从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串;
3、每个节点的所有子节点包含的字符都不相同。
实现方法:
(1) 从根结点开始一次搜索;
(2) 取得要查找关键词的第一个字母,并根据该字母选择对应的子树并转到该子树继续进行检索;
(3) 在相应的子树上,取得要查找关键词的第二个字母,并进一步选择对应的子树进行检索。
(4) 迭代过程……
(5) 在某个结点处,关键词的所有字母已被取出,则读取附在该结点上的信息,即完成查找。
再回到AC自动机:
AC自动机需要先了解的知识:字典树、KMP算法(其实也就是其中的构造失败指针像KMP中next函数一样比较巧妙,但是不了解也不是不行)
如果想看KMP算法的话,这插个小链接:模式匹配之BF算法与KMP算法
其中总结来说:
AC自动机算法分为3步:构造一棵Trie树,构造失败指针和模式匹配过程。
下面内容就是转载的大佬的博客:https://www.bestsort.cn/2019/04/28/402
下面开始用图学习ac自动机吧(个人比较喜欢放图,能用一张图解决的绝不叨叨)
首先给定模式串"ash",“shex”,“bcd”,“sha”,然后我们根据模式串建立如下trie树:
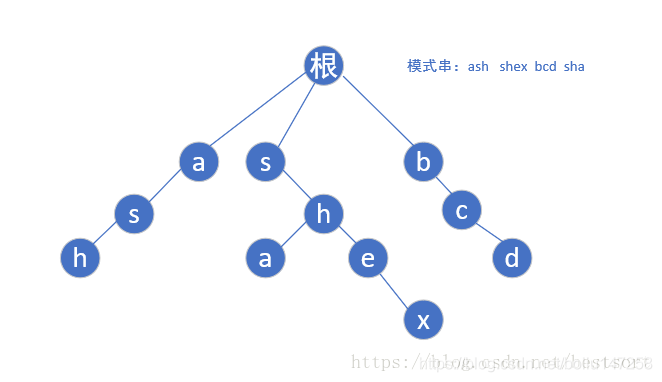
然后我们再了解下一步:
ac自动机,就是在tire树的基础上,增加一个fail指针,如果当前点匹配失败,则将指针转移到fail指针指向的地方,这样就不用回溯,而可以路匹配下去了.(当前模式串后缀和fail指针指向的模式串部分前缀相同,如abce和bcd,我们找到c发现下一个要找的不是e,就跳到bcd中的c处,看看此处的下一个字符(d)是不是应该找的那一个)
一般,fail指针的构建都是用bfs实现的
首先每个模式串的首字母肯定是指向根节点的(一个字母你瞎指什么指,指了也是头字母有什么用嘛)
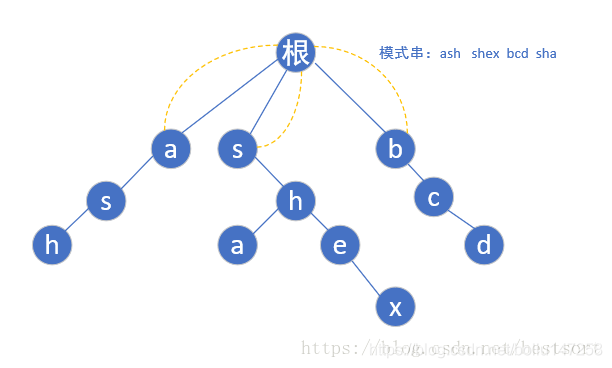
现在第一层bfs遍历完了,开始第二层
(根节点为第0层)第二层a的子节点为s,但是我们还是要从a-z遍历,如果不存在这个子节点我们就让他指向根节点(如下图红色的a)
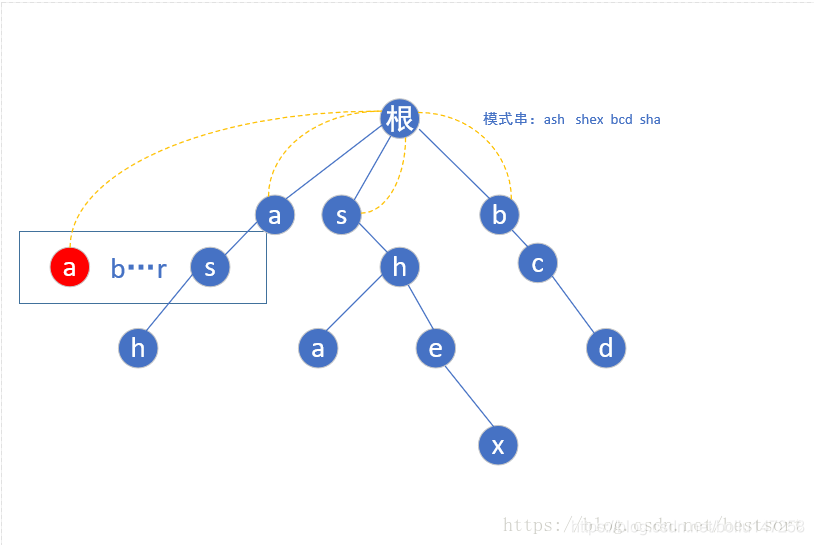
当我们遍历到s的时候,由于存在s这个节点,我们就让他的fail指针指向他父亲节点(a)的fail指针指向的那个节点(根)的具有相同字母的子节点(第一层的s),也就是这样
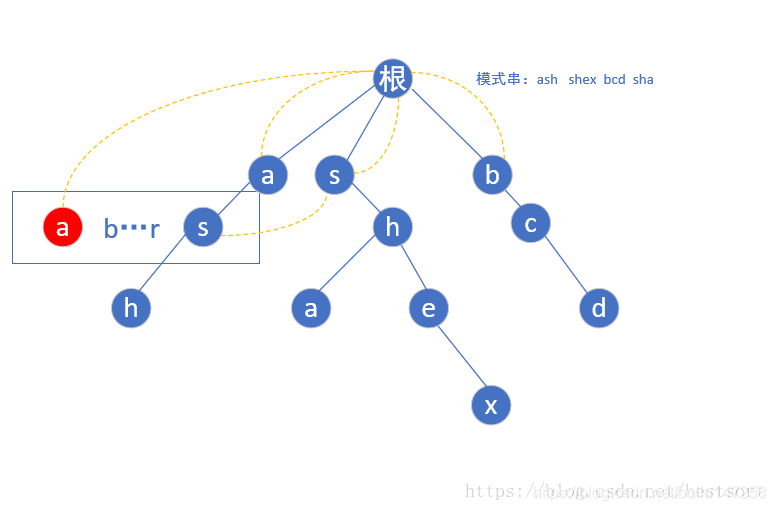
按照相同规律构建第二层后,到了第三层的h点,还是按照上面的规则,我们找到h的父亲节点(s)fail指针指向的那个位置(第一层的s)然后指向它所指向的相同字母根->s->h的这个链的h节点,如下图
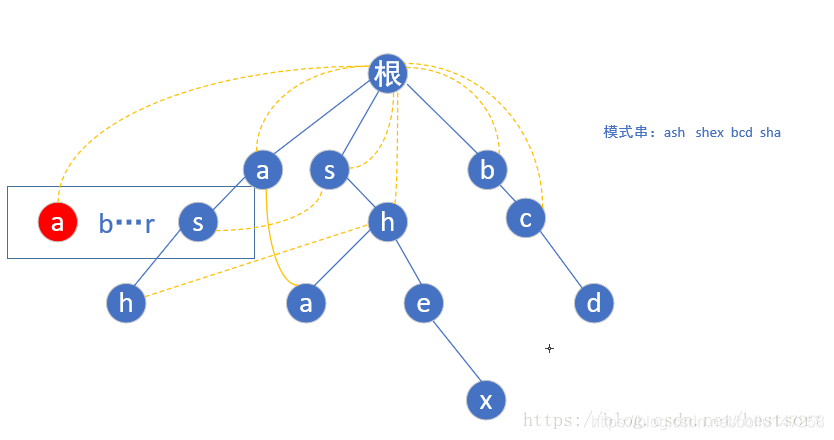
完全构造好后的树
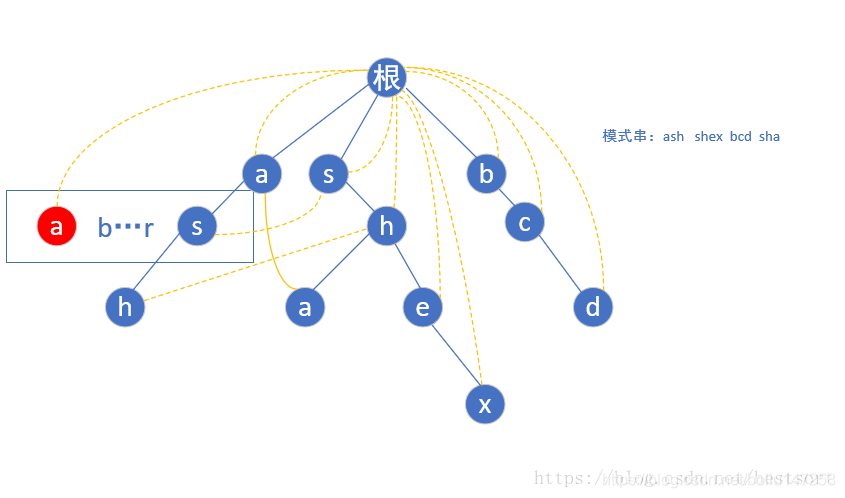
然后匹配就很简单了,这里以ashe为例
我们先用ash匹配,到h了发现:诶这里ash是一个完整的模式串,好的ans++,然后找下一个e,可是ash后面没字母了啊,我们就跳到hfail指针指向的那个h继续找,还是没有?再跳,结果当前的h指向的是根节点,又从根节点找,然而还是没有找到e,程序END

模板题: hdu 2222
开始想的肯定就只要用个KMP算法就应该能A吧,但是TLE,于是就学了AC自动机,其中好像string会A不了,还是用c的char[]数组吧,代码如下(惭愧、看着别人的模板敲的。。。。):
#include本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!