算法基础 - 2-sat问题

2-SAT问题

这个问题其实我们平时早就遇到过，只是从来没有认真的去思考这个问题的解法。这个在我们理解的时候，一般都是按照一个点开始，可以就继续，不可以就停止。

例子问题

例如我们有10个球，每个球都是编号好的，从：1 - 10这10个球，我们要从中拿出5个球，有以下要求：
并且选了1就不能选择3号球，选择了2号就不能选择4号球，选择了5号就不能选择6号。
但是这里面有个规则：{1, 2}不能同时存在。同理{3, 4}, {5 , 6}也不能存在。

这个问题很明了了，怎么解决呢？

最简单的就是枚举，首先选择一个球，看是否有规则，没有就选择下一个，有规则就按照规则选，不可以了，就回溯，一直到发现一个可以的情况，或者所有都不可以的时候，就有答案了。

可是这个方法是在太耗费时间了。更简单的办法，也就是利用图论的只是来解决。

下面是思想：

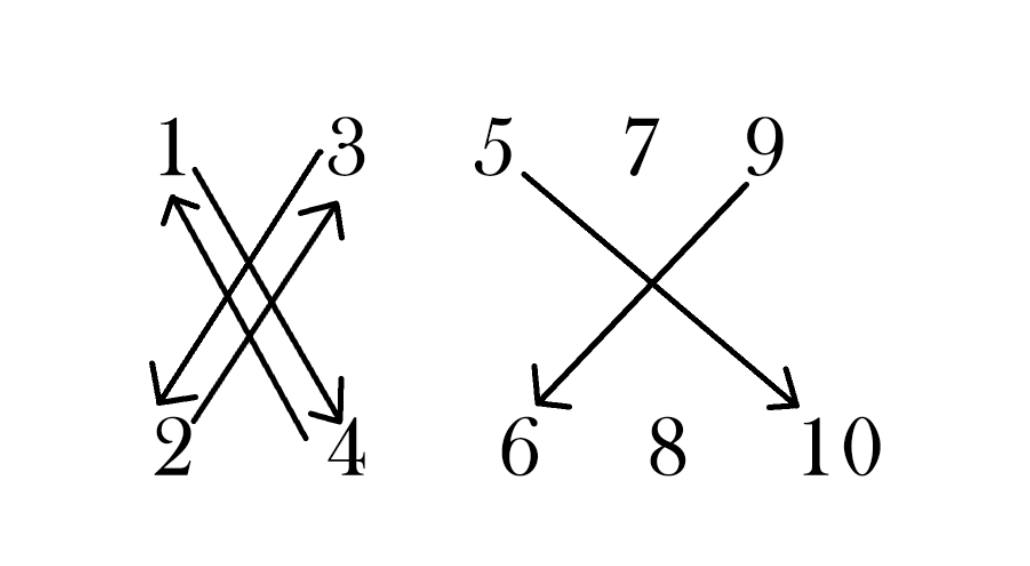
首先我们看第一个规则，1 3不能共存，那么这个时候可以得知，因为3 4必须选择一个，那么假如我们选择了1，就必须选择4了，这样我们就知道了一个边，就是1 -> 4这个边的意义就是，选择了1就必须选择4。那么假如我们选择的是3呢？那么另外一个就必须选择2。这个边就是3 -> 2了。依次类推，我们可以得到下面的图：

这样我们就得到了一个有向图，这个有向图的每条边都代表了选择了一个点，那么同时也要选择它指向的点。如果这个点是孤立的点，例如图中的7 8，那么就随便选择。那么怎么才算无解呢？

两个不相容的点，处在同一个环内，或者更通俗的说是，强连通图内。，就是无解的。

解法

上面通过例子已经讲解了如何解决这个问题：

1. 构造有向图，这个有向图是一个表示了选择了一个点，一定要选择它能够到达的点的图。
2. 对这个图求强连通图。
3. 假如有两个点处在同一个强连通图内，这两个点是必须只能选择一个的一组内的点，就不可以。
4. 否则可以

求强连通图的办法是Tarjan算法：传送门: Tarjan算法这是我之前博客里写的。

代码实现

下面这个代码是解决一个问题：

现在有一堆开关，1 2 3 4 5 ... n这么多，每个开关只有开关两个状态，现在要求，某些开关，不能同时开，或者不能同时关。

求解是否有这么一个状态，满足所有要求。

代码：

#include 
#include 
#include 
#include 
#include using namespace std;#ifndef MAXNODE
#define MAXNODE 20005
#endifint flag[MAXNODE] = {0};
int dfn[MAXNODE] = {0};
int low[MAXNODE] = {0};
int tpArr[MAXNODE] = {0};
int tpNum = 0;
int _index = 0;vector<int> graph[MAXNODE];stack<int> st;void tarjan(int n){st.push(n);flag[n] = 1;dfn[n] = ++_index;low[n] = _index;for (int i = 0; i < graph[n].size(); i++) {int cur = graph[n][i];if (dfn[cur] == 0) {tarjan(cur);low[n] = min(low[n], low[cur]);}else{if (flag[cur] == 1) {low[n] = min(low[n], dfn[cur]);}}}if (dfn[n] == low[n]) {tpNum++;do{n = st.top();st.pop();flag[n] = 0;tpArr[n] = tpNum;}while(dfn[n] != low[n]);}
}void addNode(int n1, int n2){if ((n1&1) > 0) {graph[n1].push_back(n2+1);graph[n2].push_back(n1+1);}else{graph[n1].push_back(n2-1);graph[n2].push_back(n1-1);}
}void transAddNode(int a, int b, int l){if (l == 1) {addNode(a*2, b*2);}else{addNode(a*2-1, b*2-1);}
}bool judge(int N){for (int i = 1; i <= N; i++) {if (tpArr[2*i-1] == tpArr[2*i]) {return false;}}return true;
}int main(){int M;cin>>M; //测试组数while (M--) {int N,T;cin>>N>>T; //N是开关个数，T是规则个数int a,b,c;for (int i = 0; i < T; i++) {cin>>a>>b>>c; //输入a b c分别代表开关a，开关b，已经开关状态c只有(0/1)，表示开关a,b不能同时处于状态ctransAddNode(a, b, c);}for (int i = 1; i <= 2*N; i++) {if (dfn[i] == 0) {tarjan(i);}}if(judge(N)){cout<<"Yes"<else{cout<<"No"<for (int i = 1; i <= 2*N;i++) {flag[i] = 0;dfn[i] = 0;low[i] = 0;graph[i].clear();}_index = 0;}return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！