sklearn分类指标函数sklearn.metrics.classification_repor的用法详解（含源码）

sklearn.metrics.classification_report

• • 调整方法及参数：
  • 参数说明
  • • parameters:
    • Returns:
  • 例子（官方文档）
  • • 代码
    • 分析（针对第一个例子）

该函返回一个分类指标的结果，包括样本的precision、recall、accuracy、f1-score等

调整方法及参数：

from sklearn.metrics import classification_report
sklearn.metrics.classification_report(y_true, y_pred, *, labels=None, target_names=None, sample_weight=None, digits=2, output_dict=False, zero_division='warn')

官方score

参数说明

parameters:

• y_true: 1d array-like, or label indicator array / sparse matrix. 真实标签
• y_pred：1d array-like, or label indicator array / sparse matrix.预测标签
• labels：array-like of shape (n_labels,), default=None.可选参数，要包含在报告中的可选标签索引列表，如[0,1,2]
• target_names: list of str of shape (n_labels,), default=None.可选参数，与labels对应，分类的标签名，如[‘class0’, ‘class1’]
• sample_weight: array-like of shape (n_samples,), default=None.样本的权重
• digits：int, default=2. 用于格式化输出浮点值的位数。当output dict为True时，该值将被忽略，返回值不会四舍五入。
• output_dict: bool, default=False. 如果为True则返回一个字典类型的报告
• zero_division： “warn”, 0 or 1, default=”warn”. 设置当有零除法时返回的值。如果设置为warn，则其作用为0，但也会引发警告。

Returns:

report: str or dict

返回的内容包括precision、recall、f1-score、accuracy（后文根据距离例子介绍）、averages包括macro average、weight average、Micro average。

• macro avarage: 每个标签的无权重均值；

• weighted average: 根据每个标签样本权重计算的均值

• Micro average: 所有TP、FN、FP的均值，只在多标签或者含子类的多分类问题中

例子（官方文档）

代码

from sklearn.metrics import classification_report
y_true = [0, 1, 2, 2, 2]
y_pred = [0, 0, 2, 2, 1]
target_names = ['class 0', 'class 1', 'class 2']
print(classification_report(y_true, y_pred, target_names=target_names))precision    recall  f1-score   supportclass 0       0.50      1.00      0.67         1class 1       0.00      0.00      0.00         1class 2       1.00      0.67      0.80         3accuracy                           0.60         5macro avg       0.50      0.56      0.49         5
weighted avg       0.70      0.60      0.61         5
y_pred = [1, 1, 0]
y_true = [1, 1, 1]
print(classification_report(y_true, y_pred, labels=[1, 2, 3]))precision    recall  f1-score   support1       1.00      0.67      0.80         32       0.00      0.00      0.00         03       0.00      0.00      0.00         0micro avg       1.00      0.67      0.80         3macro avg       0.33      0.22      0.27         3
weighted avg       1.00      0.67      0.80         3

分析（针对第一个例子）

首先对于y_true和y_pred画出混淆矩阵便于观察：

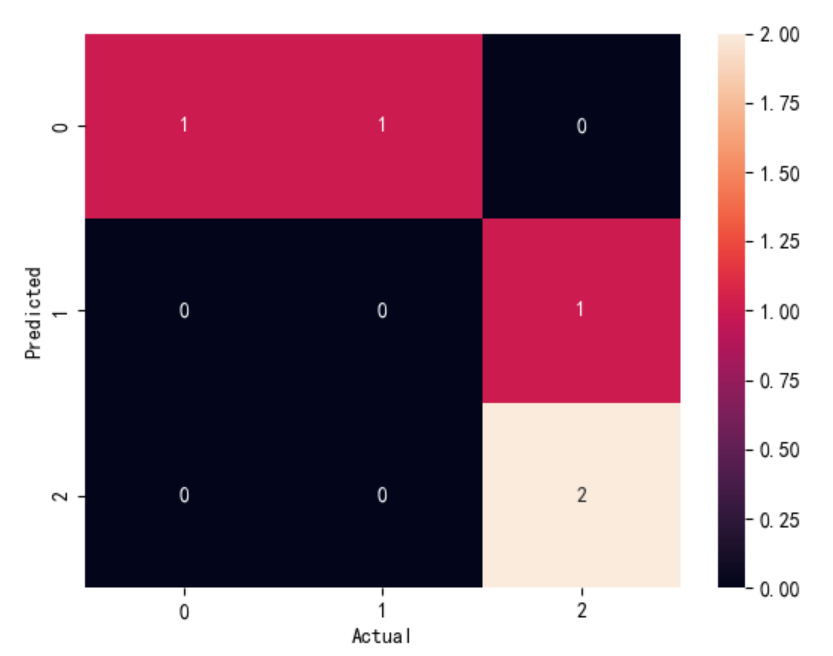
对于上图依次计算return中各个指标：

p r e c i s i o n = T P T P + F P precision = \frac{TP}{TP+FP} precision=TP+FPTP​

r e c a l l = T P T P + F N recall = \frac{TP}{TP+FN} recall=TP+FNTP​

a c c u r a c y = r i g h t a l l accuracy = \frac{right}{all} accuracy=allright​

f 1 − s c o r e = 2 1 p r e c i s i o n + 1 r e c a l l f1-score = \frac{2}{ \frac{1}{precision}+ \frac{1}{recall}} f1−score=precision1​+recall1​2​

从class0开始分析：

TP，就是实际为正样本，预测也为正样本的，为混淆矩阵的（0,0）处的值：1

FP，就是实际为负样本，被预测为正样本的，为混淆矩阵的（1,0）和（1,2）处的值：1+0=1

FN，就是实际为正样本，被预测为负样本的，为混淆矩阵的（0,1）和（0,2）处的值：0+0=0

right，就是正样本被预测为正样本，负样本被预测为负样本，为（0,0）、（1,1）、（2,2）出处的值：1+0+2=3

all，就是总体样本数：5

因此class0对应的指标依次为：

p r e c i s i o n = 1 1 + 1 = 0.5 precision = \frac{1}{1+1} = 0.5 precision=1+11​=0.5

r e c a l l = 1 1 + 0 = 1 recall = \frac{1}{1+0} = 1 recall=1+01​=1

a c c u r a c y = 3 5 = 0.6 accuracy = \frac{3}{5} = 0.6 accuracy=53​=0.6

f 1 − s c o r e = 2 1 0.5 + 1 1 = 0.67 f1-score = \frac{2}{ \frac{1}{0.5}+ \frac{1}{1}}=0.67 f1−score=0.51​+11​2​=0.67

class1&class2相关指标计算同上，注意，对于class0他自身的标签可以看作为正例，它自身之外的所有标签都是反例。

最后，macro average为对应垂直方向上的指标的非加权均值，如precision的macro average为(0.5+0+1)/3=0.5；weight average为对应的指标与所占总体样本的权重的乘积，如precision的加权average为[(1/5)x0.5+(1/5)x0+(3/5)x1]=0.7

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！