机器学习(ML)(五)——回归和聚类算法
回归和聚类算法
线性回归
线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值和因变量(目标值)之间关系进行建模的一种分析方式。
通用公式:h(w)=w1x1+w2x2+w3x3……+b=wTx+b
广义线性模型:
线性回归当中线性模型有两种,一种是线性关系,另一种是非线性关系。
线性关系:
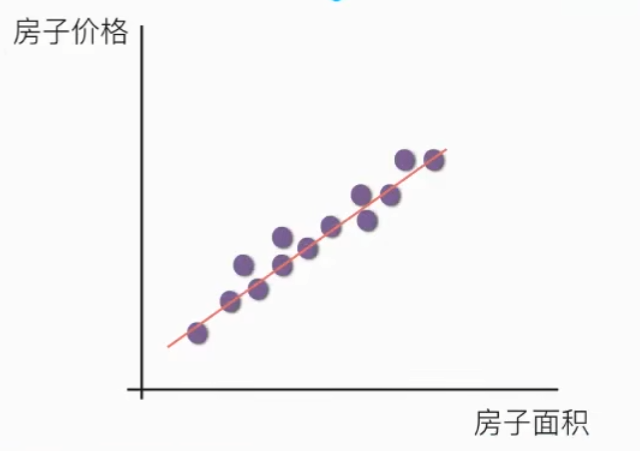
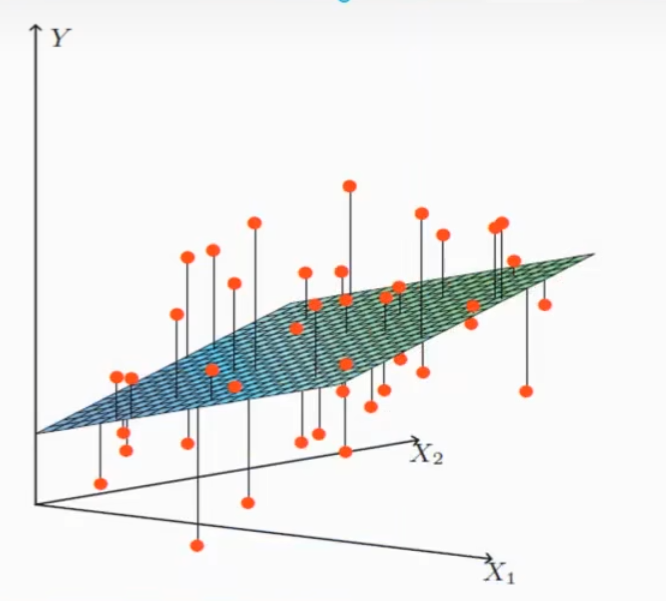
注释:单特征与目标值的关系呈直线关系,或者两个特征与目标值呈现平面的关系
非线性关系:
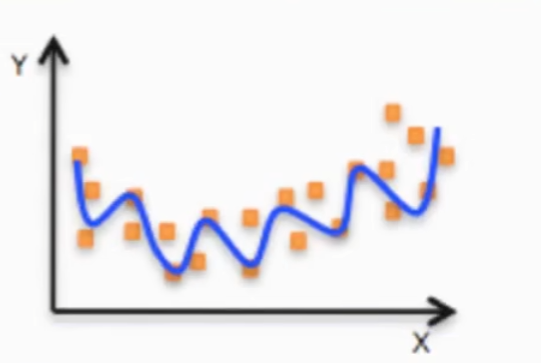
线性模型:自变量是一次的;参数是一次的
线性回归中的损失与函数优化原理
目标:
求模型参数,模型参数使得预测准确
真实关系:真实房子价格=0.0x中心区域的距离+0.04×城市一氧化氮浓度+(-0.12×自住房平均房价)
随意假定:预测房子价格=0.25×中心区域的距离+0.14×城市一氧化氮浓度+0.42×自住房平均房价
损失函数:
真实值与预测值之间的误差
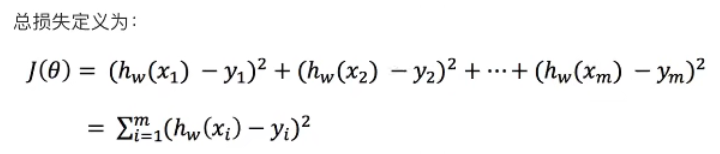
如何找到模型中的w,使得损失最小?
优化算法:
找到最小损失对应的w值
正规方程——直接求解
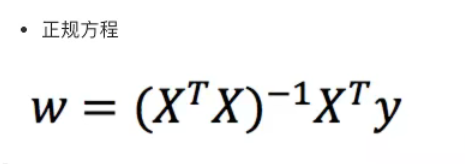
理解:X为特征值矩阵,y为目标值矩阵。直接求到最好的结果
缺点:当特征过多过复杂时,求解速度太慢并且得不到结果
梯度下降——不断试错,改进
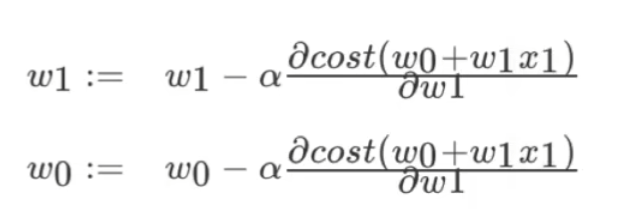
使用方法:
sklearn.linear_model.LinearRegression(fit_intercept=True)
#通过正规方程优化
#fit_intercept:是否计算偏置
#LinearRegression.coef_:回归系数
#LinearRegression..intercept_:偏置
sklearn.linear_model.SGDRegressor(loss="squared_loss",fit_intercept=True,learning_rate ='invscaling',eta0=0.01)
#SGDRegressor类实现了随机梯度下降学习,它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。
#loss:损失类型;loss=”squared_loss'”:普通最小二乘法
#fit_intercept:是否计算偏置
#learning_rate string,optional
#学习率填充
'constant':eta etao
'optimal':eta =1.0/(alpha *(t to))[default]
'invscaling':eta etao/pow(t,power_t)power_.t=0.25:存在父类当中
#对于一个常数值的学习率来说,可以使用learning_rate='constant',并使用eta0来指定学习率。
#SGDRegressor.coe_:回归系数
#SGDRegressor.intercept_:偏置
波士顿房价预测
流程分析:
流程:
1)获取数据集
2)划分数据集
3)特征工程:
无量纲化一标准化
4)预估器流程
fit()–>模型
coef_
intercept_
5)模型评估
from sklearn.datasets import load boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor
def linear1():
#正规方程的优化方法对波士顿房价进行预测
#1)获取数据boston=load boston()
#2)划分数据集x_train,x_test,y_train,y_test= train_test_split(boston.data,boston.target,random_state=22)
#3)标准化transfer=Standardscaler()x train=transfer.fit_transform(x_train)x_test=transfer.transform(x test)
#4)预估器estimator=LinearRegression()estimator.fit(x_train,y_train)
#5)得出模型print("正规方程-权重系数为:\n",estimator.coef_)print("正规方程-偏置为:\n",estimator.intercept_)
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!