【机器学习】Momentum梯度下降

梯度下降是机器学习中用来使模型逼近真实分布的最小偏差的优化方法。
在普通的随机梯度下降中，参数的更新是按照如下公式进行的：

W = W - αdW
b = b - αdb

其中α是学习率，dW、db是cost function对w和b的偏导数。

如图，在梯度下降过程中， 从某一点开始的梯度下降过程是曲折的，并不是直接走向中心点，而是需要浪费很多时间折来折去，这样的速度就会变慢，直接解决的方法就是增大学习率，但是学习率变大后可能会引起梯度下降的振荡现象，怎么样解决这个问题呢？

有一个梯度下降法叫做动量梯度下降，具体实现过程：

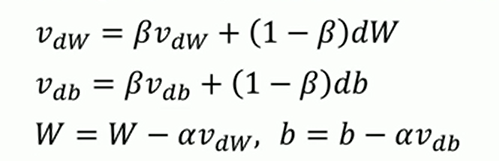
这个就是动量梯度下降的参数更新公式。
我们可以看出，在这个公式中，并不是直接减去αdW和αdb，而是计算出了一个vdW和vdb。

上图中的前两行公式叫做指数加权平均。使用这个公式，可以将之前梯度下降过程的dW和db联系起来，不再是每一次梯度都是独立的情况。其中β是可以自行设置的超参数，一般情况下默认为0.9（也可以设置为其他数值）。β代表了现在的vdW和vdb与之前的1 / (1 - β)个vdW和vdb有关。0.9就是现在的vdW和vdb是平均了之前10次的vdW和vdb的结果。

此时的梯度不再只是当前数据的梯度，而是有一定权重的之前的梯度。

而由于动量积攒了历史的梯度，如点P前一刻的梯度与当前的梯度方向几乎相反。因此原本在P点原本要大幅徘徊的梯度，主要受到前一时刻的影响，而导致在当前时刻的梯度幅度减小。
 直观上讲就是，要是当前时刻的梯度与历史时刻梯度方向相似，这种趋势在当前时刻则会加强；要是不同，则当前时刻的梯度方向减弱。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！