POJ 2942 Knights of the Round Table tarjan求双连通分量+判断奇环

题目：https://vjudge.net/problem/POJ-2942#author=0

大意：

国王要在圆桌上召开骑士会议，但是有若干对骑士之间互相憎恨。

出于各种各样奇怪的原因，每次开会都必须有如下要求：

1、相互憎恨的两个骑士不能坐在相邻的两个位置。

2、为了让投票表决议题时都能有结果（不平票），出席会议的骑士数必须是奇数。

如果有某个骑士无法出席任何会议，则国王会为了世界和平把他踢出骑士团。

现在给定骑士总数 n，以及 m 对相互憎恨的关系，求至少要踢掉多少个骑士。

（注意只有一个骑士是不能出席会议的）

首先就是先将可以相邻的骑士左右连，构建一幅图

出席会议的骑士需要连成环，所以需要在图上尽可能找出不同的环，并且这些环的节点有奇数个，然后将那些未能参与组成奇数环的点统计起来就是答案。（因为这些点组不成奇数环就表示无论如何都不能出席会议）

首先需要尽可能的找到环，然后去判断这个环是不是奇数环。

找环的话用tarjan求图的点双联通分量，就可以找出不同的环。但是此时这些环都是尽可能的最大的环，如何判断环上的人可以参加会议呢？

当然不可以单纯的直接判断这个大环是奇还是偶数环，因为：

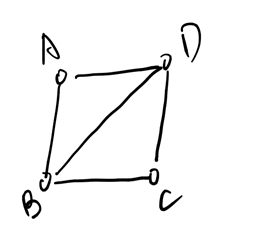
这个ABCD大环可以分成ABD  BDC 两个奇数环，他们都可以去参加会议。

引理：只要某个点双连通分量中存在奇环，那么这个点双连通分量上的所有点都处在至少一个奇环里面。

那么就只需要知道大环内是否包含奇环就可以了

判断奇数环的方法用奇偶染色法

#include
#include
#include
#include
#include
using namespace std;
const int maxn = 1e3 + 7;
const int maxm = 1e6 + 7;
int Head[maxn], Nxt[maxm], To[maxm], vis[maxn];
int heat[maxn][maxn];
int low[maxn], dfn[maxn], st[maxn], flag, color[maxn];
int tot, n, m, cnt, id, st_ind;
int ok[maxn];
vector V[maxn];
void init() {memset(Head, 0, sizeof(Head));memset(heat, 0, sizeof(heat));memset(dfn, 0, sizeof(dfn));memset(vis, 0, sizeof(vis));memset(ok, 0, sizeof(ok));memset(color, 0, sizeof(color));for (int i = 1; i <= n; i++) V[i].clear();tot = 1;cnt = id = st_ind = 0;
}
void add_edge(int fro, int to) {Nxt[++tot] = Head[fro];To[tot] = to;Head[fro] = tot;
}
void tarjan(int now) {if (Head[now] == 0) {++cnt;V[cnt].push_back(now);return;}dfn[now] = low[now] = ++id;st[++st_ind] = now;for (int i = Head[now]; i; i = Nxt[i]) {int &to = To[i];if (!dfn[to]) {tarjan(to);low[now] = min(low[now], low[to]);if (dfn[now] <= low[to]) {++cnt;int obj;do {obj = st[st_ind--];V[cnt].push_back(obj);} while (obj != to);V[cnt].push_back(now);}}else low[now] = min(low[now], dfn[to]);}
}
void dfs(int beg,int opt) {color[beg] = opt;for (int i = Head[beg]; i; i = Nxt[i]) {int to = To[i];if (vis[to] != vis[beg]) continue;if (color[to] == 0) dfs(to, 3 - opt);else if (color[to] == color[beg]) {//!!不是 to==3-begflag = 1;return;}if (flag == 1) return;}
}
int main() {while (cin >> n >> m, n) {init();int fro, to;for (int i = 1; i <= m; i++) {scanf("%d %d", &fro, &to);heat[fro][to] = 1;heat[to][fro] = 1;}for (int i = 1; i <= n; i++)for (int j = i+1; j <= n; j++) if (!heat[i][j]) //可以相邻的建边add_edge(i, j), add_edge(j, i);for (int i = 1; i <= n; i++) //因为可能整体不连通if(!dfn[i]) tarjan(i);int ans = 0;for (int i = 1; i <= cnt; i++) {if (V[i].size() == 1) {continue;}for (int j = 0; j < V[i].size(); j++) {vis[V[i][j]] = i, color[V[i][j]] = 0;}flag = 0;dfs(V[i][0], 1); //奇偶染色法if (flag == 1) {for (int j = 0; j < V[i].size(); j++) ok[V[i][j]] = 1;}}for (int i = 1; i <= n; i++) if (!ok[i]) ans++;printf("%d\n", ans);}
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！