梯度下降简单介绍
ps:本文章仅用于自身学习,主要为了自己去理解,可能写的不好,所以建议移步其他文章
一,什么是梯度下降?
梯度本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模),可理解为导数。
梯度下降就是使函数的点向着梯度方向变化小、变化率慢的点移动,可理解为使导数的绝对值趋向于零
二,梯度下降用于解决什么?
梯度下降大多用于求解损失函数的最小值,损失函数 是评定模型预测结果与实际情况的匹配度的。损失函数越大,匹配度越小,即误差越大;损失函数越小,匹配度越大,即误差越小。
下面给出损失函数的一般形式:
其中为数据组数,
为实际结果,
为模型预测的结果,通过求取损失函数的最小值即可使模型相对来说更准确。
三,具体理论实现与代码实现
前面我们知道梯度下降是使函数的点向着梯度方向变化小、变化率慢的点移动,即让函数的导数趋近于零,求取函数的极小值。那么具体如何实现呢?
这里先以一元函数为例:
设一元函数,现在要用梯度下降法求取它的极小值
第一步:先导入必要的库
import numpy as np
import matplotlib.pyplot as plt第二步:定义函数,求取导数
def f(x):return (x - 2.5)**2 + 3
def df1(x)return 2*x - 5同时导数也可以这样求取
def df2(x):return (f(x + 0.00001) - f(x - 0.00001)) / (2 * 0.00001) 第三步:设定学习率,误差范围
,以及初始位置
n=0.9
e=0.01
x0=1第四步:开始迭代
此处再具体分析:
1、令,求导数
2、判断导数的绝对值是否小于e。若小于e,停止循环;反之,继续执行循环,执行下一步
3、更新
4、重复上述步骤直至符合条件
x = x0
while 1:dy = df2(x)if abs(dy) < e: breakx = x - n*dyprint(x)第五步:得出结果
极小值点x=2.495466528151911
极小值为f(x)=3.0000205523669976
点的实际变化图像
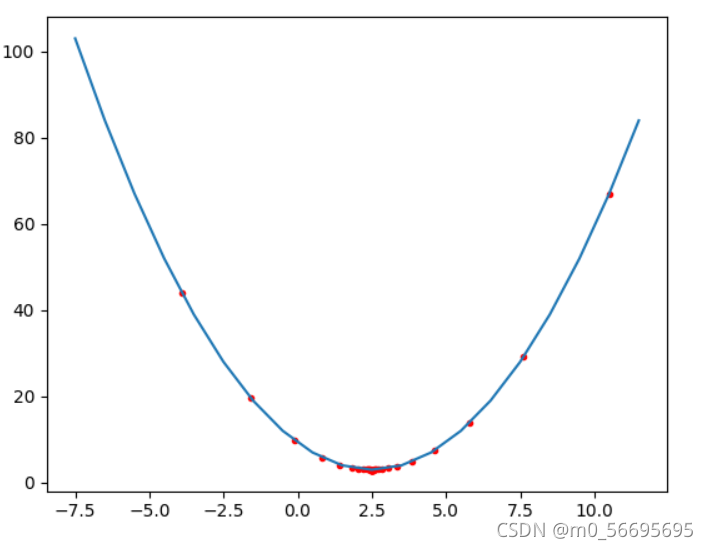
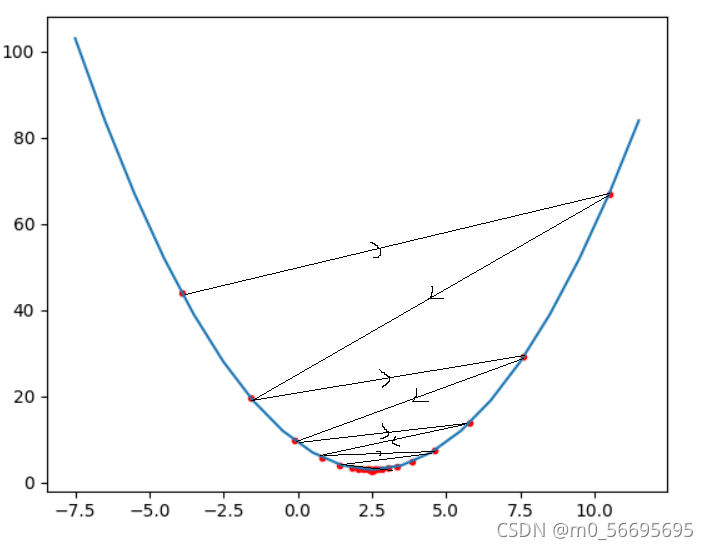
可以看出函数的点朝着极小值和导数绝对值小的方向移动
四,梯度下降的的三种训练方式
一,全量梯度下降法(Batch gradient descent)
将数据集的全部数据都拿来训练,优点是模型预测的更准确,但比较耗时
二、随机梯度下降法(Stochastic Gradient Descent)
每次迭代随机抽取数据集的一组部分数据拿来训练,耗时较短,但误差较大
三、小批量梯度下降法
每次迭代抽取数据集的多个数据进行训练,用此方法耗时短误差小
五、上述例题的完整代码
# 用梯度下降法手工写出下列式子的求解过程,用 python 编程实现,并画图。
# y=(x-2.5)²+3
import numpy as np
import matplotlib.pyplot as plt
def f(x):return pow(x-2.5,2) + 3
def df1(x):return 2*x - 5
def df2(x):return (f(x + 0.00001) - f(x - 0.00001)) / (2 * 0.00001)n=0.9
e=0.01
x0=-7.5x = x0
xs = []
while 1:dy = df2(x)if abs(dy) < e: breakx = x - n*dyxs.append(x)
#开始绘图
xs1 = np.arange(-7.5,12.5)
xs2= np.array(xs)
plt.plot(xs1,f(xs1))#绘制曲线图
plt.scatter(xs2,f(xs2),color = "red",marker=".")#绘制散点图
plt.show()print("极小值点x={}".format(x))
print("极小值为f(x)={}".format(f(x)))本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!