二分法求方程根

二分法是计算机上的一种常用算法，下面列出计算步骤：

step1：计算  在有根区间 [a,b] 端点处的值 

step2:  计算  在区间中点（a+b）/2 处的值 

step3:  若 ==0，则 即是根

           若,则

           若,则

代码如下：

erfen.m

%有根区间[a,b] 函数 y=x^2-2;调用了erfenhanshu();
a=1;b=6;e=10;
cnt=0;
while(e>0.1)cnt=cnt+1;fa=erfenhanshu(a);fb=erfenhanshu(b);c=(a+b)/2;fc=erfenhanshu(c);if(fc==0)c;e=0;break;elseif(fa*fc<0)b=c;elsea=c;endende=b-a;
end    
disp("迭代的次数, 求得的根");
cnt
c
%绘图
x=1:.1:5;
y=x.*x-5;
plot(x,y,'r');
hold on;
x=1:0.1:5;
y=0.*x;
plot(x,y,'b');

erfenhanshu(x):

function[y]=erfenhanshu(x);
y=x*x-5;
end

迭代了6次，求得结果为2.1719

图片：

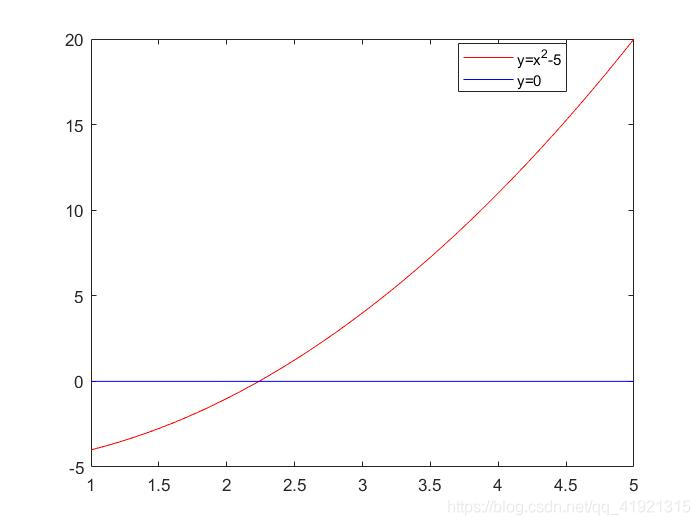
增加了注释:

clc;clear all;
a=input('输入左区间，a=');
b=input('输入左区间，b=');
err=input('输入精度: err=');%有根区间[a,b],误差为err
e=10000;    %初始误差
while(e>err)fa=erfenhanshu(a);%f(x)在点a处的值f(a)fb=erfenhanshu(b);%f(x)在点b处的值f(b)c=(a+b)/2;% c是区间[a,b]的中点fc=erfenhanshu(c);% f(x)在点c处的值f(c)if(fc==0)        %如果 f(c)==0,那么点c就是根c;e=0;break;elseif(fa*fc<0) %如果 f(a)*f(c)<0,那么区间可以缩短为[a,c],即b=c;b=c;else        %如果 f(b)*f(c)<0,那么区间可以缩短为[c,b],即a=c;a=c;endende=b-a;          %误差e=b-a;
end    
disp("求得的根");
c
function[y]=erfenhanshu(x)y=x*x*x/3-x;
end

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！