tarjan算法求强连通分支
Tarjan算法详解
近期做数据结构课程设计,遇到了有向图的强连通分支的问题,网上采用的是基于深度优先遍历的tarjan算法,在考了许多博客后,还是有些迷,在思考了一番后,终于明白了,所以写了这篇文章。
首先,明确以下几点。
-
tarjan算法基于深度优先遍历。使用时,会用到两个栈。一个栈用于DFS,(如果是递归的tarjan算法,是隐式地使用了系统堆栈);另一个栈就是要保存连通分支的信息了,以下说的栈都是这个栈。
-
每个顶点有两个属性标记,DFN和LOW。
- DFN:记录的是DFS的时间次序,在遍历到该节点时确定,后续不需要更改
- LOW:记录能够回溯到的栈中元素的DFN的最小值(比较难理解)
-
明确状态
- 入栈,开始访问一个节点时,DFN == LOW == 当前是第几个访问到的序列号index
- 出栈,当DFN == LOW,且该节点没有出边时,得到了子树的根,将其以及之后的(栈中)所有节点出栈,这样便找到了一个强连通分支
- 其他,当DFN != LOW,且该节点没有出边时,不做任何操作,只是回退到上一个节点,继续处理
-
算法过程
对一个顶点进行tarjan时,主要是对出边的检查
在进行tarjan(i)时,先后进行两步操作:边的检查、LOW和DFN的检查- 先进行边的检查
如果有这样的边:i->j,有以下三种情况:- 状态1,j未被访问过
- 进行tarjan(j)
- 更新i的LOW值:Low(i)=min( Low(i) ,Low(j))
- 状态2,j访问过且在栈中
更新i的LOW值:Low(i)=min( Low(i) ,DFN(j)) - 状态3,j访问过
不进行更新
- 状态1,j未被访问过
- 当i的出边均访问完后,检查DFN和LOW
- 相等,该点及其后点出栈,得到了连通分支
- 不相等,回退到上一个节点
最后,需要执行循环,防止不只有一个弱连通分支
- 先进行边的检查
-
c++代码
#include
#include using namespace std;int G[7][7]; //以邻接矩阵表示6*6的图,索引0不用
int index=0;
int DFN[7];
int LOW[7];
int C=1; //标记连通分支
stack tarjan; //储存节点的栈
int component[7]; //记录最终节点所属的强连通分支
bool isInStack[7]; //是否在栈中
bool visited[7]; //是否访问过void init(){int i[8]={1,1,2,3,3,4,4,5};int j[8]={2,3,4,4,5,1,6,6};for(int m=1;m<=6;m++) //初始化邻接矩阵for(int n=1;n<=6;n++)G[m][n]=0;for(int k=0;k<8;k++) //增加边G[i[k]][j[k]]=1;for(int k=1;k<=6;k++){component[k]=0;isInStack[k]=false;visited[k]=false;}
}void Tarjan(int i){DFN[i]=LOW[i]=++index;visited[i]=true;isInStack[i]=true;tarjan.push(i);for(int j=1;j<=6;j++){if(G[i][j]==0)continue;if(!visited[j]){ //状态1,未被访问Tarjan(j);LOW[i]= LOW[i] 运行输出:
1 : 3
2 : 3
3 : 3
4 : 3
5 : 2
6 : 1
- 算法模拟
接下来模拟上述过程。
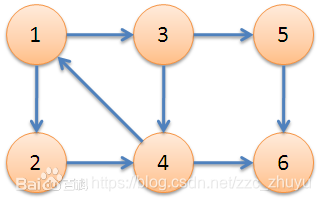
为方便,先记录下所有顶点的DFN和LOW的初始情况
| index | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| DFN | 1 | 6 | 2 | 5 | 3 | 4 |
| LOW | 1 | 6 | 2 | 5 | 3 | 4 |
tarjan(1):有边1->3(状态1),tarjan(3):有边3->5(状态1),tarjan(5):有边5->6(状态1),tarjan(6):DFN == LOW ,出栈得到连通分支{6}回退到上一个顶点5Low(5)=min( Low(5) ,Low(6))= 3DFN == LOW ,出栈得到连通分支{5}回退到上一个顶点3Low(3)=min( Low(3) ,Low(5))= 2有边3->4(状态1),tarjan(4):有边4->6(状态3)有边4->1(状态2):Low(4)=min( Low(4) ,DFN(1))= 1DFN != LOW回退到上一个顶点3Low(3)=min( Low(3) ,Low(4))= 1DFN != LOW回退到上一个顶点1Low(1)=min( Low(1) ,Low(3))= 1有边1->2(状态1),tarjan(2):有边2->4(状态2):Low(2)=min( Low(2) ,DFN(4))= 5DFN != LOW回退到上一个顶点1Low(1)=min( Low(1) ,Low(2))= 1DFN == LOW ,,出栈得到连通分支{1,3,2,4}
上述过程循环
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!