时间序列研(part4)--虚假回归
学习笔记,仅供参考,有错必纠
文章目录
- 时间序列
- 虚假回归
- 用蒙特卡罗模拟方法分析相关系数的分布
- t统计量的分布
- 简单回归中 β 1 = 0 \beta_1=0 β1=0的拒绝概率与变量单积阶数的关系
- 样本容量与虚假回归的关系(回归变量均为I(1)变量)
- 虚假回归的直观解释
时间序列
虚假回归
用蒙特卡罗模拟方法分析相关系数的分布


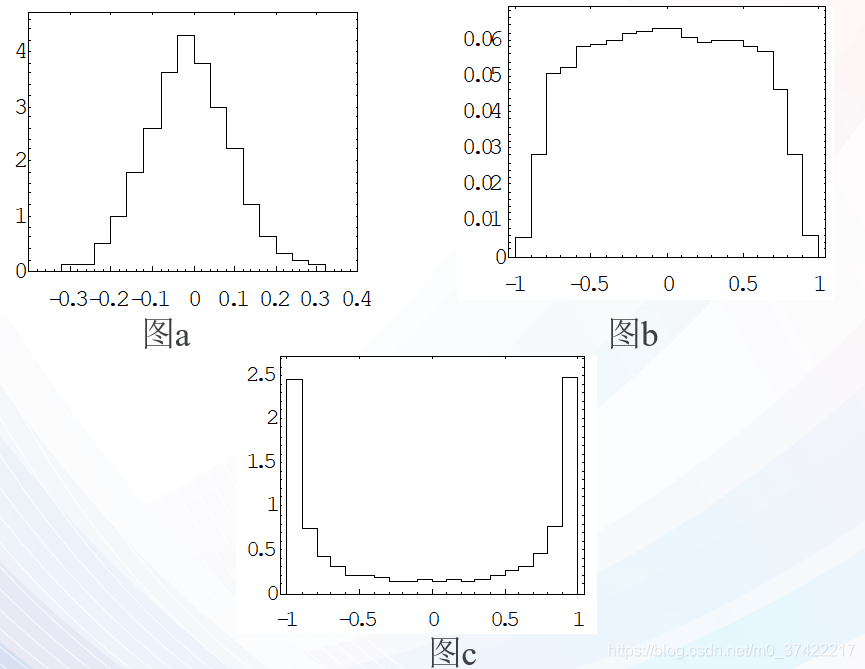
问题的严重性在于当变量非平稳时,认为R服从的是正态分布,但实际上R服从的却是图b和图c那样的倒U和U型分布,因此增加了拒绝概率,本不相关的两个变量结论却是相关.
t统计量的分布
有如下数据生成系统:

| 组距 | 频数 | 组距 | 频数 | 组距 | 频数 |
|---|---|---|---|---|---|
| [-20,-18) | 1 | [-6,-4) | 11 | [8,10) | 10 |
| [-18,-16) | 0 | [-4,-2) | 28 | [10,12) | 7 |
| [-16,-14) | 0 | [-2,0) | 30 | [12,14) | 4 |
| [-14,-12) | 4 | [0,2) | 21 | [14,16) | 4 |
| [-12,-10) | 3 | [2,4) | 21 | [16,18) | 2 |
| [-10,-8) | 6 | [4,6) | 11 | [18,20) | 3 |
| [-8,-6) | 17 | [6,8) | 17 |
t ( β 1 ^ ) t(\hat{\beta_1}) t(β1^)的分布见下图:
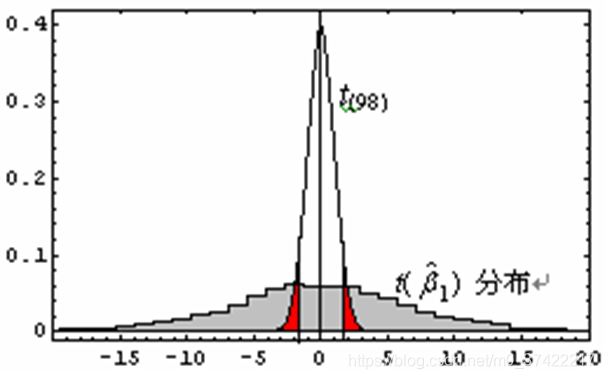
显然,上述条件下的 t ( β 1 ^ ) t(\hat{\beta_1}) t(β1^)不服从t分布。若在5%的检验水平上使用t检验,零假设b1 = 0将以(200-30-21)/200=0.745的比率被错误拒绝。这就是虚假回归问题。
简单回归中 β 1 = 0 \beta_1=0 β1=0的拒绝概率与变量单积阶数的关系
| 两变量的单积阶数 | P ( t ( ( ^ β 1 ) ) > 2 ) P(t(\hat(\beta_1)) > 2) P(t((^β1))>2) |
|---|---|
| I(0) 与I(0) | 0.045 |
| I(1) 与I(1) | 0.77 |
| I(2) 与I(2) | 0.95 |
样本容量与虚假回归的关系(回归变量均为I(1)变量)
随样本容量变化,拒绝 β 1 = 0 \beta_1=0 β1=0的概率,即 P ( t ( ( ^ β 1 ) ) > 2 ) P(t(\hat(\beta_1)) > 2) P(t((^β1))>2),如图所示:
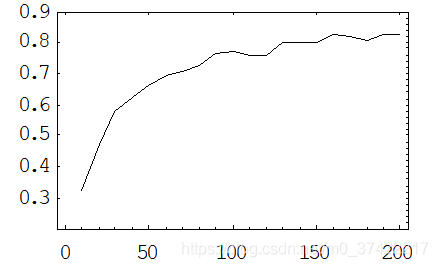
虚假回归的直观解释

Phillips(1986)利用泛函中心极限定理从理论上对虚假回归问题进行了分析:
- 用OLS法估计所得结果不能用通常的假设检验给以解释;
- 当样本容量趋于无穷大时,相应于模型的DW统计量的分布趋近于零;
- 实际中,若所估计的回归模型的DW值非常小,而表示模型拟合优度的多重确定系数 R 2 R^2 R2的值又非常大,说明所拟合的回归模型是有问题的.
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!