IFDS开山之作：Precise Interprocedual Dataflow Analysis via Graph Reachability

• <>
• 这篇文章是IFDS的开山之作，当然该作者还有一篇文章讲IDE的：《Precise interprocedural dataflow analysis with applications to constant propagation》；在实际的开源工具中，一般IFDS/IDE会同时支持
• 将数据流问题转化为图可达问题，是这篇文章的精华；另外，summary等思想也值得学习
• 值得注意的是，本文最初提出的IFDS算法，仍然有效率上的不足，比如它需要pre-compute爆炸超级图，实际上是需要一定开销的。而实际在分析过程中求解时用到的路径大小其实是远小于爆炸超级图的大小。所以有很多计算、空间是浪费了。
• 所以后来的文章有提出该算法的在实际应用中的扩展，大概的意思是边的计算是on the fly的，也就是边求解边计算边。
• 再后来，Sparse Value Flow的概念很火，也有提出Sparse IFDS概念。
• 再后来，也有提出利用磁盘核外计算，降低IFDS内存开销
• 最后，这篇文章是IFDS的经典文章，非常值得学习，认真研究后其实并不难。
  
  
• 这篇文章对应的算法演示：IFDS论文算法精解：应用于污点分析的例子

---

23年4月补充：如果要用简单的几句话来概括IFDS的贡献或者思想的话，我觉得可以这么总结：

1. IFDS将经典数据流分析的IN-OUT/GEN以集合传播数据流的方式，转换为图上的边(dataflow fact)的构造问题。(将经典数据流分析的Transfer Function转换为图可达/传递必包的问题)
2. 给出了Interprocedural control flow graph图上的括号匹配的算法

---

一大类的流程间数据流问题，通过将其转化为一种特殊的图可达性问题，能够在多项式时间复杂度内被精确求解。

对于这类数据流问题的唯一约束就是：数据流事实必须是有限集，数据流转换函数必须在交汇操作（Union或Intersection）上是可分配的。

这类数据流问题包括但不限于经典的seperable problems（也叫gen/kill，bit-vector），比如reaching definitions，avariable expressions，live variables。除此之外，也包括non-seperable problem，比如truly-live variables，copy propagation，possibly-uninitialized variables。

标题中的Precise什么意思？

我们知道流程内分析的精确定义就是MOP（Meet-Over-All-Paths），遍历所有路径并在路径末尾作交汇（理论模型）。

流程间分析的精确定义就是MVP（Meet-Over-All-Valid-Paths），遍历所有合理的路径，并在路径末尾作交汇。所谓合理，就是数据流从流程内返回时需返回给正确的调用点。

什么是IFDS（Interprocedual, finite, distribute, subset problem）？

• 数据流事实D是一个有限（ F inite）集合
• 数据流的transfer function: D 2 → D 2 D^{2} \rightarrow D^{2} D2→D2 在交汇操作（ S et的Union或者Intersection）上是可分配的（ D istribute）

使用IFDS框架要明确两个问题：

• 编码数据流问题以符合IDFS框架的要求（流程间，有限，分配性，子集）
• 数据流问题的编码需要与程序语言的语义保持一致

首先，编码数据流问题可能会损失精度（比如没有考虑别名等情况）。但是IFDS框架对这个问题的求解并不会损失精度。

定义2.1

在IFDS中，程序用一个有向图 G ∗ G^* G∗表示 ，图 G ∗ G^* G∗ 叫做超图(supergraph)
G ∗ = ( N ∗ , E ∗ ) G^* = (N^*, E^*) G∗=(N∗,E∗)

G ∗ G^* G∗ 由子流图 G 1 , G 2 , G 3 , . . . , G i , i ∈ P G_1, G_2, G_3, ..., G_i, i \in P G1​,G2​,G3​,...,Gi​,i∈P的集合组成, P为程序流程(procedure)的集合； G m a i n G_{main} Gmain​ 为入口main函数的流图

对于每个 G i G_i Gi​, 都有一个唯一的start节点 s p s_p sp​, 唯一的exit节点 e p e_p ep​，就是流程内控制流图的定义。其它的非调用相关的普通节点和流程内控制流图的一样。

对于调用节点，被表示成两个节点：call node 和 return-site node.对于流程p来说，这两个节点组成的集合表示为 C a l l p Call_p Callp​, R e t p Ret_p Retp​；而对于全程序的call，return-site node集合，表示为$Call$, $Ret$

除了一般的流程内流图边之外，每个 G i G_i Gi​多了几条边：

• call-to-return-site edge: 从call node到return-site node之间的流程内的边
• call-to-start edge: 从call node到callee的start node之间的流程间的边
• exit-to-return-site: 从callee的exit node到caller的return-site node之间的流程间的边

call-to-return-site边让IFDS能处理局部变量和参数?。

call-to-return-site和exit-to-return-site边能让局部变量在调用点的数据流和被调用流程末端的全局数据流做合并。

下面是超图的一个例子：

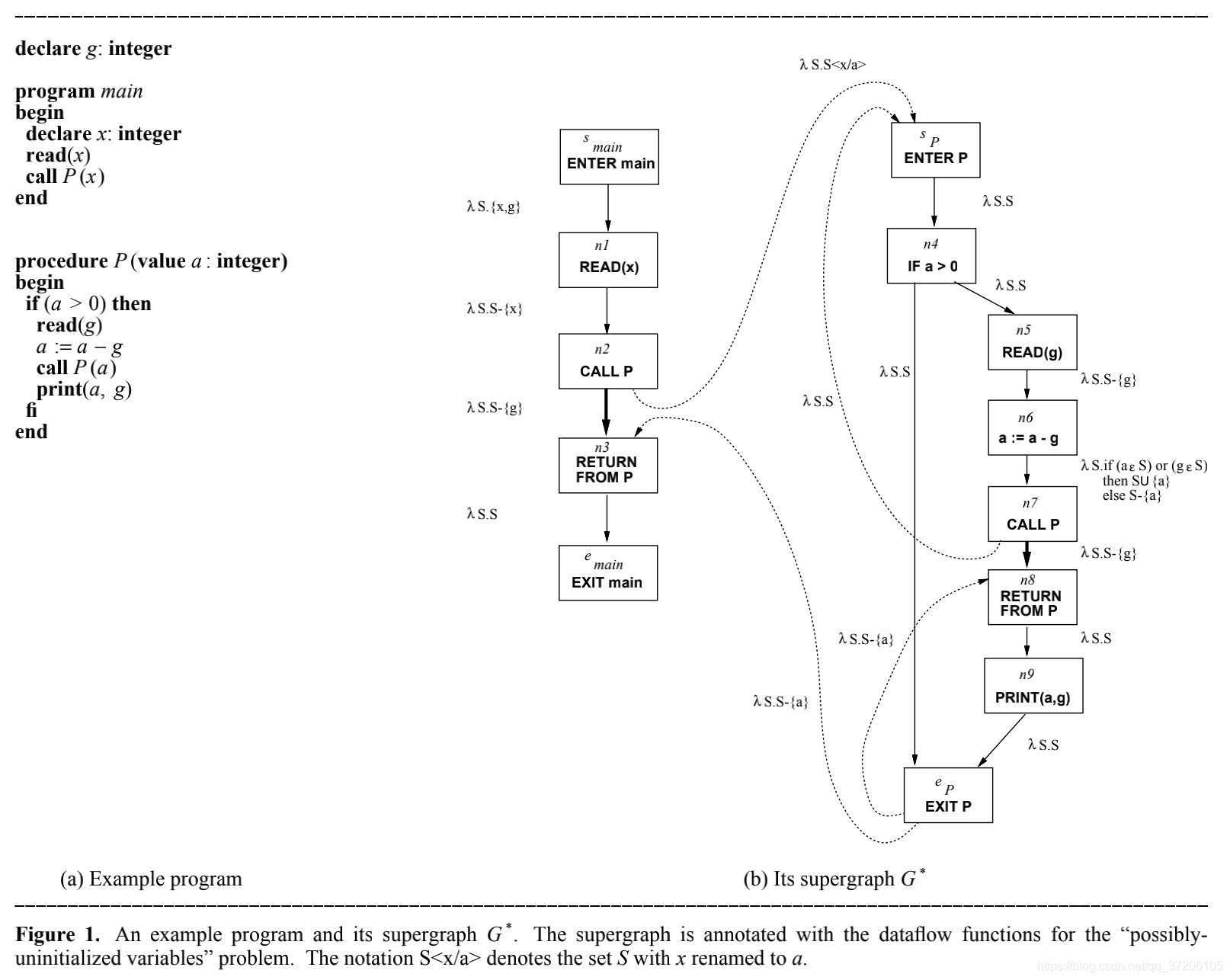
为了方便起见，我们使用集合的名字来表示其大小。

• 用$Call$ 表示Call node集合的大小
• 用$N$, $E$ 分别表示 N ∗ N^* N∗, E ∗ E^* E∗ 的大小

定义2.2

从节点m到n之间长度为j的路径由j条边组成，表示为:
[ e 1 , e 2 , . . . , e j ] 1 ≤ i ≤ j − 1 , e i 的 t a r g e t 就是 e i + 1 的 s o u r c e \begin{aligned} & [e1, e2, ..., e_j] \\ & 1 \le i \le j-1, e_i的target就是e_{i+1}的source \end{aligned} ​[e1,e2,...,ej​]1≤i≤j−1,ei​的target就是ei+1​的source​

定义2.3

让 G ∗ G^* G∗ 的每个调用点编个号，给个索引 $i$, 调用点记作 c i c_i ci​, 与之对应的call-to-start边被标记为 ( i (_i (i​, 与之对应的exit-to-return-site边被标记为 ) i )_i )i​

• 对于同一流程内的两个节点m, n. 从m到n的路径是同级合理的（same-level valid path），当且仅当这条路径上的边的标记序列是满足括号匹配的。可以用如下的正则语言表示 m a t c h e d → ( i m a t c h e d ) i m a t c h e d f o r 1 ≤ i ≤ C a l l ∣ ε matched \rightarrow \ (_i\ matched \ )_i \ matched \ \ \ \ \ for \ 1 \le i \le Call \\ | \ \varepsilon matched→ (i​ matched )i​ matched     for 1≤i≤Call∣ ε
  • 对于流程内的两个节点之间的路径，如果存在调用，必须满足括号匹配最终返回到同一流程中来。
• 更一般地，为了表示 G ∗ G^* G∗ 中的任意两个节点间路径是合理路径（valid path），他们之间的路径上的边的标记序列需要满足：
• v a l i d → v a l i d ( i m a t c h e d f o r 1 ≤ i ≤ C a l l ∣ m a t c h e d valid \rightarrow \ valid \ \ (_i\ matched \ \ \ \ \ for \ 1 \le i \le Call \\ | \ matched valid→ valid  (i​ matched     for 1≤i≤Call∣ matched
  • 也就是说对于流程间的路径它们不一定满足括号匹配，也可能是一直往深处调用，而没有返回，这也算是一条合理的路径；

这个其实在图上很容易理解，不过作者通过形式化的方式来解释什么是流程间一条合理的路径。

作者给出路径的定义，然后在路径上的边打标记，这条路径上标记组成的序列需要满足一定的规则(文法)，才是一条合理的路径。

我们将m, n之间所有合理的路径集合记作：IVP(m, n)

IVP: interprocedurally valid path

定义2.4

一个IFDS问题(简称IP)是个5元组：

I P = ( G ∗ , D , F , M , ⊓ ) IP \ = \ (G^*, \ D, \ F, \ M, \ \sqcap ) IP = (G∗, D, F, M, ⊓)

• $G\ast$ 为超图，定义2.1
• $D$ 是有限集合
• F ⊆ 2 D → 2 D F \subseteq 2^D \rightarrow 2^D F⊆2D→2D 是一个可分配的转换函数
• M : E ∗ → F M: E^* \rightarrow F M:E∗→F 是一个从 G ∗ G^* G∗ 中边到数据流转换函数之间的映射
• meet操作 $\sqcap$ 要么是Union要么是Intersection

定义2.4是对D有简化，实际上，由于每个procedure都有不同的变量，一般也有不同的数据流事实定义域。所以实际处理的过程中对每个流程p都有一个可能不同的数据流定义域 D p D_p Dp​

论文接下来只考虑IFDS问题中meet操作为union的。

一般来说，

• must-be-X问题是一个intersection IFDS问题，而may-not-be-X是一个union IFDS问题。
• 对于每个节点 n ∈ N ∗ n \in N^* n∈N∗, must-be-X问题的解是may-not-be-X问题解在D上的补给

定义2.5

I P = ( G ∗ , D , F , M , ⊓ ) IP \ = \ (G^*, \ D, \ F, \ M, \ \sqcap ) IP = (G∗, D, F, M, ⊓) 是一个IFDS问题，

• q = [ e 1 , e 2 , . . . , e j ] q = [e_1, e_2, ..., e_j] q=[e1​,e2​,...,ej​] 是 G ∗ G^* G∗ 中非空路径，则关于路径q的path function表示为 p f q = f j ∘ . . . ∘ f 2 ∘ f 1 pf_q = f_j \circ ... \circ f_2 \circ f_1 pfq​=fj​∘...∘f2​∘f1​，其中 f o r a l l i , 1 ≤ i ≤ j , f i = M ( e i ) for\ all\ i, \ 1 \le i \le j, \ f_i = M(e_i) for all i, 1≤i≤j, fi​=M(ei​)
• 路径长度为0的path function为单位函数(identity function) $\lambda x.x$

定义2.6

I P = ( G ∗ , D , F , M , ⊓ ) IP \ = \ (G^*, \ D, \ F, \ M, \ \sqcap ) IP = (G∗, D, F, M, ⊓) 是一个IFDS问题，IP的meet-over-all-valid-paths解是由 M V P n MVP_n MVPn​ 值的集合组成。

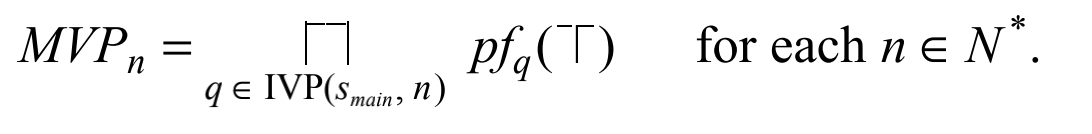
用自然语言描述这个公式，就是：

从main函数的start节点 s m a i n s_{main} smain​开始，到节点$n$的所有路径组成的集合为Q。

对于所有的$q\in Q$, 求解该路径的path function，输入为top。然后将所有路径求得的path function值进行meet。所得的解就是节点n的IFDS解。

下面是我理解MVP的大概逻辑的非正式代码，其实理解起来很容易。

Map<Edge, TransferFunction> M; 	   // M为IP定义的映射关系：edge -> TransferFunctionData mvp(Node n) {Set<Path> Q = ...;      	   // s_main到节点n的所有合理路径集合Data result = T;  			   // 节点n的ifds解for path in Q {Data pathResult = pathFunction(path, T);result = meet(result, pathResult); // meet即为IP定义的交汇操作}return result;
}/*** 定义2.5定义的 Path Function*/
Data pathFunction(Path p, Data initData) {// 获取组成路径的边Edge[] edges = p.getEdges();Data result = initData;for edge in edges {TransferFunction transfer = M[edge]; // TransferFunction 为IP定义的 Fresult = transfer.flow(result);		 // flow方法即为应用转换函数}
}

定义3.1

定义2.5，2.6已经给出了怎么用理想的方式（即MVP: meet-over-all-valid-paths）去求解IFDS解。

这里我们介绍怎么去将这种求解过程转化为图可达性问题。

再看到IP的定义： I P = ( G ∗ , D , F , M , ⊓ ) IP \ = \ (G^*, \ D, \ F, \ M, \ \sqcap ) IP = (G∗, D, F, M, ⊓)

• $G\ast$ 为超图，定义2.1
• $D$ 是有限集合
• F ⊆ 2 D → 2 D F \subseteq 2^D \rightarrow 2^D F⊆2D→2D 是一个可分配的转换函数
• M : E ∗ → F M: E^* \rightarrow F M:E∗→F 是一个从 G ∗ G^* G∗ 中边到数据流转换函数之间的映射
• meet操作 $\sqcap$ 要么是Union要么是Intersection

既然是数据流的可达性问题，而数据的转换是通过转换函数来进行操作的，那么就研究怎么去表示F，以至于能够表示数据流的可达性问题。

下面是定义

这里讨论怎么去表示可分配性函数： 2 D → 2 D 2^D \rightarrow 2^D 2D→2D ：

每个函数都能被表示成一个图，它最多有 ( D + 1 ) 2 (D + 1)^2 (D+1)2 条边，或者表示成(D + 1) × (D + 1) 的邻接矩阵

下面的例子都假定f，g作用在 2 D → 2 D 2^D \rightarrow 2^D 2D→2D, 并且它们是关于 $\cup$ 可分配的。

f用一个二元关系来表示： R f ⊆ ( D ∪ { 0 } ) × ( D ∪ { 0 } ) R_f \subseteq (D \cup \{0\}) \times (D \cup \{0\}) Rf​⊆(D∪{0})×(D∪{0})，它的定义为：

R f = { ( 0 , 0 ) } ∪ { ( 0 , y ) ∣ y ∈ f ( ∅ ) } ∪ { ( x , y ) ∣ y ∈ f ( { x } ) a n d y ∉ f ( ∅ ) } \begin{aligned} R_f = &\ \ \{(0, 0)\} \\ \cup &\ \ \{(0, y) | y \in f(\empty)\} \\ \cup &\ \ \{(x, y) | y \in f(\{x\}) \ and \ y \notin f(\empty) \} \end{aligned} Rf​=∪∪​  {(0,0)}  {(0,y)∣y∈f(∅)}  {(x,y)∣y∈f({x}) and y∈/f(∅)}​

R f R_f Rf​可以用图来表示，它有2(D + 1)个节点, 每个表示是D中的一个元素，其中0表示空集。

从定义可知

• R f R_f Rf​ 中不可能存在 ( x , 0 ) ∈ R f , x ∈ D (x, 0) \in R_f, x \in D (x,0)∈Rf​,x∈D
• 如果存在 ( 0 , y ) ∈ R , y ∈ ( D ∪ { 0 } ) (0, y) \in R, y \in (D \cup \{0\}) (0,y)∈R,y∈(D∪{0}), 那么不存在 $(x,y)\in R,x\in D$

定义3.2

上述 R ⊆ ( D ∪ { 0 } ) × ( D ∪ { 0 } ) R \subseteq (D \cup \{0\}) \times (D \cup \{0\}) R⊆(D∪{0})×(D∪{0}) 可表示成函数 [ [ R ] ] : 2 D → 2 D [[R]]: 2^D \rightarrow 2^D [[R]]:2D→2D, 函数的定义为:
[ [ R ] ] = λ X . ( { y ∣ ∃ x ∈ X , ( x , y ) ∈ R } ∪ { y ∣ ( 0 , y ) ∈ R } ) − { 0 } [[R]] = \lambda X.(\ \{y \ | \ \exists x \in X, (x, y) \in R \ \} \cup \{\ y \ | \ (0, y) \in R\ \}\ ) - \{0\} [[R]]=λX.( {y ∣ ∃x∈X,(x,y)∈R }∪{ y ∣ (0,y)∈R } )−{0}

定理3.3

$[[R]]=f$

接下来证明两个关系 R f , R g R_f, R_g Rf​,Rg​ 的表示对应于函数的组合$$g\circ f$$

定义3.4

给定两个关系 R f ⊆ S × S R_f \subseteq S \times S Rf​⊆S×S 和 R g ⊆ S × S R_g \subseteq S \times S Rg​⊆S×S ，它们的关系组合 R f ; R g ⊆ S × S R_f; R_g \subseteq S \times S Rf​;Rg​⊆S×S 被定义成如下：

R f ; R g = ( x , y ) ∈ S × S ∣ ∃ z ∈ S , ( x , z ) ∈ R f a n d ( z , y ) ∈ R g R_f; R_g = {(x, y) \in S \times S \ |\ \exists z \in S, (x, z) \in R_f \ and \ (z, y) \in R_g} Rf​;Rg​=(x,y)∈S×S ∣ ∃z∈S,(x,z)∈Rf​ and (z,y)∈Rg​

这其实就有关系的传递那味道了， 如果应用f(x)得到：x -> z，应用g(z)得到z -> y。那么意思就是应用$g\circ f(x)$ 能够得到y。

定理3.5

对于所有的 f , g ∈ 2 D → 2 D , [ [ R f ; R g ] ] = g ∘ f 对于所有的f, g \in 2^D \rightarrow 2^D, [[R_f; R_g]] = g \circ f 对于所有的f,g∈2D→2D,[[Rf​;Rg​]]=g∘f

3.4和3.5就表示：对于任意两个在 2 D → 2 D 2^D \rightarrow 2^D 2D→2D 上可分配的函数，都能够被表示成一个图(关系)，它最多有 ( D + 1 ) 2 (D+1) ^ 2 (D+1)2 条边。

引理3.6

给定一个函数集合
f i : 2 D → 2 D , ∀ i , 1 ≤ i ≤ j f_i: 2^D \rightarrow 2^D \ , \ \forall i, \ 1 \le i \le j fi​:2D→2D , ∀i, 1≤i≤j ,

f j ∘ f j − 1 ∘ . . . ∘ f 2 ∘ f 1 = [ [ R f 1 ; R f 2 ; . . . ; R f j ] ] f_j \circ f_{j-1} \circ \ ... \ \circ f_2 \circ f_1 = [[R_{f_1}; R_{f_2}; ... ; R_{f_j}]] fj​∘fj−1​∘ ... ∘f2​∘f1​=[[Rf1​​;Rf2​​;...;Rfj​​]]

从数据流问题到可行路径的可达问题

定义3.7

令 I P = ( G ∗ , D , F , M , ⊓ ) IP \ = \ (G^*, \ D, \ F, \ M, \ \sqcap ) IP = (G∗, D, F, M, ⊓) 是一个IFDS问题，定义爆炸超级图（exploded supergraph） G I P # G_{IP}^\# GIP#​

G I P # = ( N # , E # ) G_{IP}^\# = (N^\#, E^\#) GIP#​=(N#,E#)

N # = N ∗ × ( D ∪ { 0 } ) N^\# = N^* \times (D \cup \{0\}) N#=N∗×(D∪{0})

E # = { < m , d 1 > → < n , d 2 > ∣ ( m , n ) ∈ E ∗ a n d ( d 1 , d 2 ) ∈ R M ( m , n ) } E^\# = \{\ \ \rightarrow \ \ | \ (m, n) \in E^* \ and \ \ (d_1, d2) \in R_{M_{(m, n)}} \ \ \ \} E#={ <m,d1> → <n,d2> ∣ (m,n)∈E∗ and  (d1​,d2)∈RM(m,n)​​   }

爆炸图的节点是以pair的形式：。

• 每个节点n被爆炸成D+1个节点
• 每条边根据关系 R f R_f Rf​的表示也被爆炸成一定数量的边

数据流问题IP就对应了一个在图 G I P # G_{IP}^\# GIP#​ 上单源可行路径的可达性问题，单源对应的source node为 < s m a i n , 0 > <smain​,0>

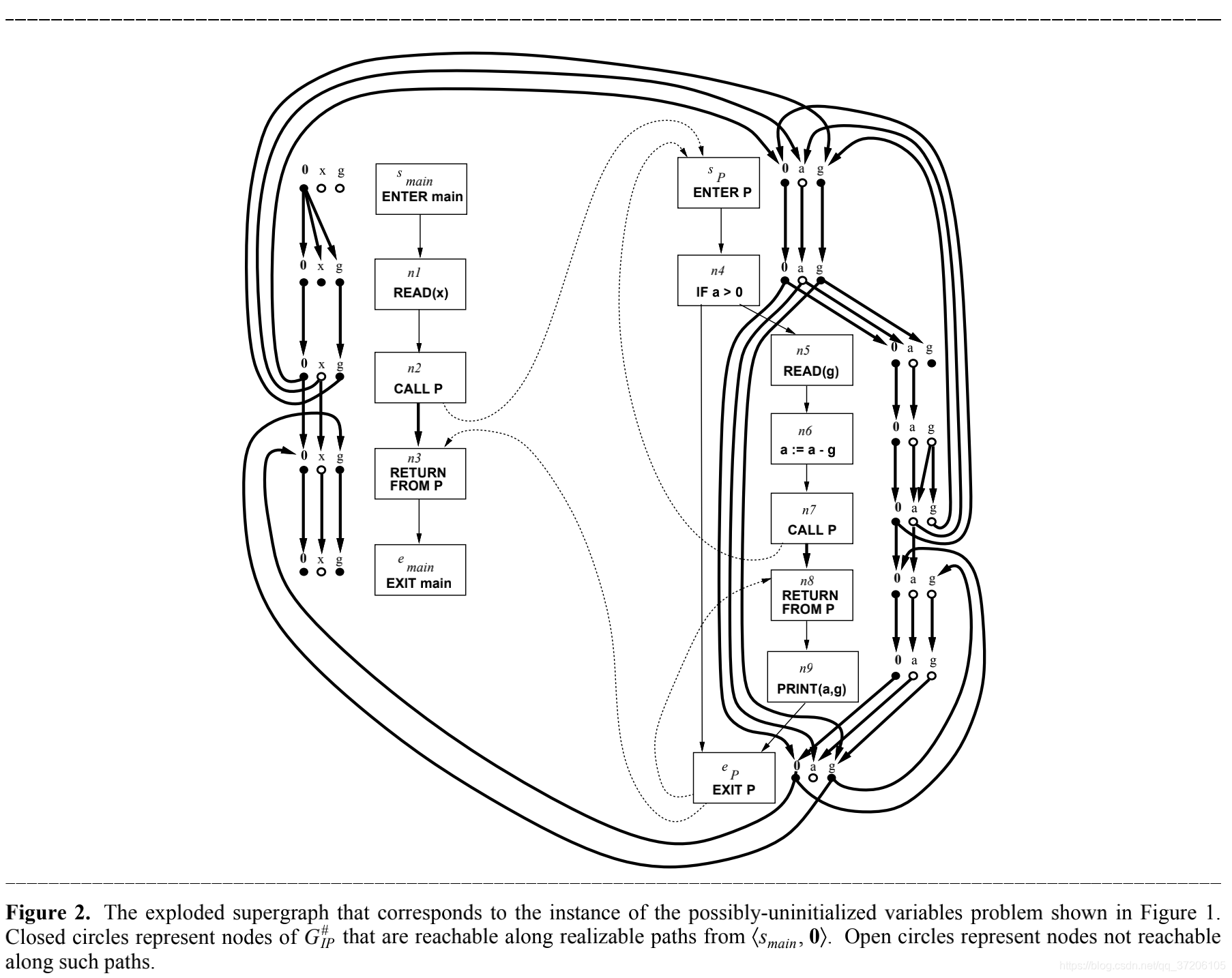
定理3.8

G I P # = ( N # , E # ) G_{IP}^\# = (N^\#, E^\#) GIP#​=(N#,E#) 是IFDS问题 I P = ( G ∗ , D , F , M , ⊓ ) IP \ = \ (G^*, \ D, \ F, \ M, \ \sqcap ) IP = (G∗, D, F, M, ⊓) .

令 n ∈ N ∗ , 那么 d ∈ M V P n , 当且仅当图 G I P # 上存在一条从 < s m a i n , 0 > 到 < n , d > 的可行路径 令n \in N^*, 那么d \in MVP_n, 当且仅当图G_{IP}^\# 上存在一条从到的可行路径 令n∈N∗,那么d∈MVPn​,当且仅当图GIP#​上存在一条从<smain​,0>到<n,d>的可行路径

这个定理就告诉我们，我们能够通过求解图 G I P # G_{IP}^\# GIP#​ 上的可行路径的可达性问题，找到IP的 MVP解。

有效的求解可行路径可达性问题的算法

这个算法是动态规划算法，它会tabulates same-level的可行路径。这个算法叫做Tabulation Algorithm

该算法用到的一些函数需要指出：

• returnSite: 映射 call node -> 与之对应的return-site node
• procOf: 映射 node -> 与之对应的enclosing函数
• calledProc: 映射 call node -> callee的函数名
• callers: 映射 函数名 -> 调用到该函数的call nodes

该算法使用PathEdge集合用来记录path edges的存在，这表示在 G I P # G_{IP}^\# GIP#​ 中 same-level 可行路径的子集。特别地，一个path edge的source总是以 < s p , d 1 > <sp​,d1​>形式表示的节点，以至于一条从 < s m a i n , 0 > <smain​,0>到 < s p , d 1 > <sp​,d1​> 的可行路径存在。换句话说，从 < s p , d 1 > <sp​,d1​> 到 < n , d 2 > <n,d2​> 的一条path edge表示一条从 < s m a i n , 0 > <smain​,0>到 < s p , d 1 > <sp​,d1​> 的可行路径的后缀。

该算法使用SummaryEdge集合来记录summary edges的存在，它表示从 < n , d 1 > <n,d1​> 到 < r e t u r n S i t e ( n ) , d 2 > <returnSite(n),d2​> 的 same-level 可行路径。（其中$n\in Call$）。在数据流问题被求解时，summary edges表示调用后的数据流值如何依赖调用前的数据流值 的（部分）信息。

该算法是一个worklist算法，它会不断地累积PathEdge和SummaryEdge集合。算法初始化时的path edges为表示长度为0的从 < s m a i n , 0 > 到 < s m a i n , 0 > 到 <smain​,0>到<smain​,0> 的same-level可行路径。在每次迭代的时候，算法会推导出其它的path edges和summary edges。

一旦已知有一个从 < s m a i n , 0 > 到 < s p , d > 到 <smain​,0>到<sp​,d> 的path edge存在，那么一个 < s p , d > → < s p , d > \ \rightarrow <sp​,d> →<sp​,d>的path edge 被插入WorkList。形为 < s p , d > → < s p , d > \ \rightarrow <sp​,d> →<sp​,d>的path edge表示从 < s m a i n , 0 > 到 < s p , d > 到 <smain​,0>到<sp​,d> 的可行路径的0长度的后缀。

• 2021-08-05: 这个算法还没完整的看完，过两天待续补完这篇文章…
• 2021-09-08: 算法已经完整地洗脑式地写了个PPT过了一遍，看具体情况，再更新到博客
• 2021-09-23: 这篇文章对应的算法演示：IFDS论文算法精解：应用于污点分析的例子

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！