【空间点绕任意直线旋转公式】
罗德里格旋转公式是计算三维空间中，一个向量绕旋转轴旋转给定角度以后得到的新向量的计算公式。百度百科
其表达式为：
其中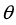
代表旋转角度，
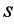代表旋转轴的单位方向向量。
对于空间中任意直线L，对其描述需要两个变量，即单位方向向量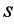与其上一点
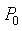。对于空间中任一点
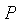，绕直线L逆时针旋转θ后成为点
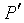。而点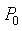绕直线L旋转后不变，故对于向量，根据罗德里格斯公式有：
故点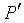
坐标可以表示为
具体代码可以参考其他博主的：
1.matlab版本：(214条消息) 三维空间任意一点绕任意轴线旋转_空间一点绕任意直线旋转_Marc Pony的博客-CSDN博客
2.python版本：(214条消息) 计算一个点 (结构式) 围绕一条直线旋转angle角之后的空间坐标，Python实现_空间点绕直线旋转的坐标_wangeil007的博客-CSDN博客
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！