Lossless CNN Channel Pruning via Gradient Resetting and Convolutional Re-parameterization

论文地址：https://arxiv.org/abs/2007.03260
代码地址：https://github.com/DingXiaoH/ResRep.

因为CNN的表征能力取决于宽度，所以通道剪枝往往会降低性能。传统的通道剪枝通过对参数进行惩罚来提高剪枝的鲁棒性，这样会在剪枝之前就降低性能。作者受神经生物学关于记忆和遗忘的独立性启发，将CNN再参数化为记忆部分(目标函数)和遗忘部分(惩罚损失)，记忆部分学习保持性能，遗忘部分学习提高效率。对前者使用SGD训练再参数化模型，对后者使用带惩罚梯度的新的更新规则，实现了结构的稀疏性，将再参数化模型转换成更窄的原始结构。在ImageNet上将具有76.15%的top1精度的ResNet50无损地剪枝成43.9%的FLOPs，在CIFAR10上将93.71%的ResNet56无损地剪枝成47.09%的FLOPs。

对于基于训练的剪枝方法，可以从两方面进行评估：

1. Resistance。训练的目的是向模型中引入一些必需的属性，如结构的稀疏性，然后进行剪枝，但是这些性质可能会引起模型性能下降。对于能抵制这种退化，保持高精度的模型具有高抵抗力。
2. Prunability。经过训练的模型如果保持较高的剪枝率且性能下降较低，则具有高剪枝能力。
   作者提出了ResRep方法可以实现这种完美剪枝。

ResRep

具体来说，就是用conv-BN-compactor将原始模型的conv-BN重新参数化，其中，压缩器(compactor)是$1\times 1$的卷积层。在训练过程中，只对compactor施加惩罚梯度，并让一些通道的梯度归零。经过训练可以得到更窄的compactor，在经过等效变换成原始结构，得到最终的剪枝后的模型。
ResRep和传统的基于惩罚的通道剪枝方法对比如下图。

对于卷积层，有：

其中，输入 I ∈ R N × C × H × W I \in R^{N\times C\times H\times W} I∈RN×C×H×W，卷积核 K ∈ R D × C × K × K K \in R^{D\times C\times K\times K} K∈RD×C×K×K，输出 O ∈ R N × D × H ′ × W ′ O \in R^{N\times D\times H'\times W'} O∈RN×D×H′×W′，偏置 b ∈ R D b \in R^{D} b∈RD，映射$B(\cdot )$将偏置$b$转换成 N × D × H ′ × W ′ N\times D\times H'\times W' N×D×H′×W′。
对于conv-BN层，均值$\mu$，标准差$\sigma$，放缩因子$\gamma$，偏置$\beta$，则有

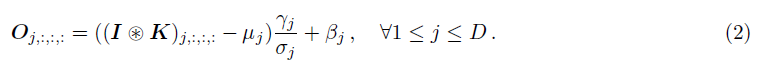
剪枝后，剪枝通道 P ( i ) ⊂ { 1 , 2 , . . . , D } P^{(i)} \subset \{1,2, ...,D\} P(i)⊂{1,2,...,D}，幸存的通道 S ( i ) = { 1 , 2 , . . . , D } \ P ( i ) S^{(i)}=\{1,2, ...,D\} \backslash P^{(i)} S(i)={1,2,...,D}\P(i)。剪枝保留了conv(i)的 S ( i ) S^{(i)} S(i)个的输出通道及对应的conv(i+1)的输入通道。得到卷积核：

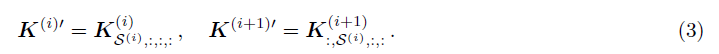
Convolutional Re-parameterization

记忆部分——卷积的再参数化，即利用$1\times 1$的compactor Q对conv-BN层再参数化。在开始训练时，令Q初始化为单位矩阵，conv-BN层初始化为base模型的权值，这样能够得到与base模型相同的输出；在梯度重置训练时，利用阈值 $ϵ$ ( $ϵ$ 取值为 1 × 1 0 − 5 1 \times 10^{-5} 1×10−5)对compactor进行剪枝(剪掉L2范数小于 $ϵ$ 的通道)，则剪枝通道 P = { j ∣ ∣ ∣ Q j < ϵ ∣ ∣ } P=\{j| ||Q_j< \epsilon||\} P={j∣∣∣Qj​<ϵ∣∣} ，幸存通道 S = { j ∣ ∣ ∣ Q j ≥ ϵ ∣ ∣ } S=\{j| ||Q_j \geq \epsilon||\} S={j∣∣∣Qj​≥ϵ∣∣} 。剪枝后的compactor为 Q ′ = Q S , : Q' = Q_{S,:} Q′=QS,:​ 。
经过剪枝的compactor的行数明显少于列数，即 Q ′ ∈ R D ′ × D , D ′ = ∣ S ∣ Q' \in R^{D' \times D}, D'=|S| Q′∈RD′×D,D′=∣S∣ .。因此只需要找到能将conv-BN-compactor转化成卷积层的 K ′ ∈ R D ′ × C × K × K K' \in R^{D' \times C\times K\times K} K′∈RD′×C×K×K和 b ′ ∈ R D ′ b' \in R^{D'} b′∈RD′。
首先，构造一个新的conv层：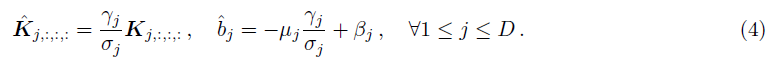
易证得：

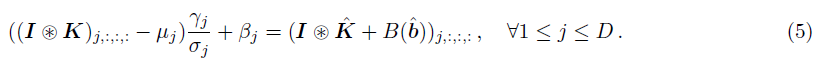
只需令：

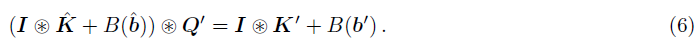
展开：

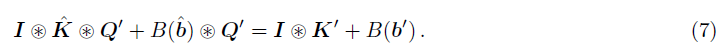
令$T(\cdot )$为一个转置函数，即将$D\times C\times K\times K$转置成$C\times D\times K\times K$，则有：

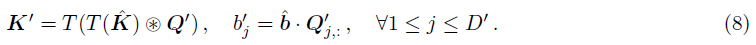
Gradient Resetting

整体目标函数为：

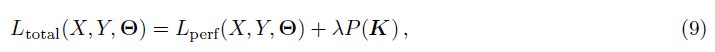
其中第一项为性能相关的目标函数，第二项为惩罚损失(如L1，L2，group Lasso)，选择group Lasso，则：

对于某个特定的通道 F = K j F=K_j F=Kj​，梯度为：

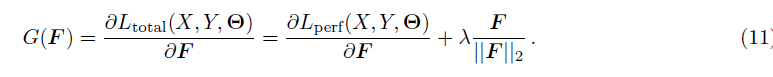
作者引入了一个mask m ∈ { 0 , 1 } m \in \{0,1\} m∈{0,1}来选择是否对通道$F$进行重置。即：

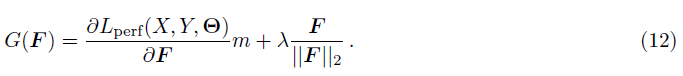
其中，$\lambda$取 1 × 1 0 − 4 1 \times 10^{-4} 1×10−4。

Experiments

在cifar10上复现实验结果：

以上结果是做了5次实验取平均。实验结果和论文结果比较接近，可以算是完美剪枝(降低不到0.01%)，并且剪枝率比论文的结果高了0.31%。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！