斐波那契数列与尾递归

斐波那契数列,又称黄金分割数列,形如0、1、1、2、3、5、8、13、21、34、……

不难发现：n>=2时，f(n) = f(n-1)+f(n2)

如果用代码来体现就是

    function f(n) {if (n <= 2) return n;return f(n - 1) + f(n - 2);}

时间复杂度分析

你会发现，如果你执行f(50),需要很久才能出结果。

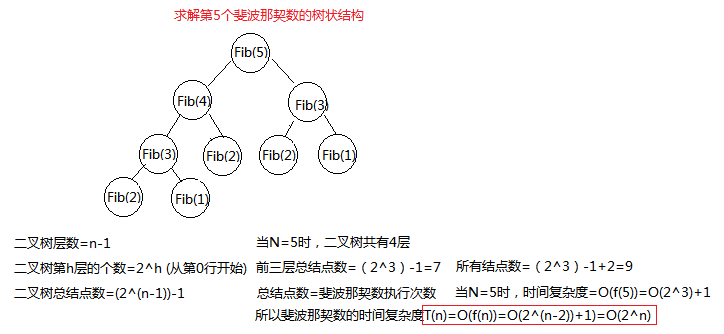
因为f(50)=f(49)+f(48)，而其中f(49)=f(48)+f(47)...如此反复，直到f(3)=f(2)+f(1) ,我们才开始计算结果；由下图可知，计算f(50)需要计算2^(50-2) + 1次，这也就不难解释需要算很久了。

反向思考

不难发现，之所以时间复杂度这么大，是因为每一次计算结果都依赖下一次的计算结果，那我们反过来思考，从后面开始算起，f(3)=f(2)+f(1)=2,f(4)=f(3)+f(2)=3...,把每一次的计算结果存起来

function f(n) {let arr = [1, 2];if (n <= 1) return arr[n];for (let i = 2; i < n; i++) {arr[i] = arr[i - 1] + arr[i - 2];}return arr[n - 1];}

又或者，方法二

function f(n) {let prev1 = 1;let prev2 = 2;if (n === 1) return prev1;if (n === 2) return prev2;let result;for (let i = 2; i < n; i++) {// result = prev1 + prev2;[prev1, prev2] = [prev2, result = prev1 + prev2]; //解构赋值更简化}return result;}

思想都是从已知开始算起，把计算过的结果保存起来，然后不断前进计算，很显然，上面两种时间复杂度为O(n)

对于方法二，如果我们改造一下，把prev1和prev2作为函数的参数，然后改造成递归会是什么样？

function f(n, prev1 = 1, prev2 = 2) {if (n === 1) return prev1;if (n === 2) return prev2;[prev1, prev2] = [prev2, prev1 + prev2];return f(n - 1, prev1, prev2);}
// f(50) =20365011074

f(50)计算出来了。显然，这里的时间复杂度也为O(n)，因为参数n 只是不断递减，n=2就可以直接返回结果了。

但是其实这里也是不断返回 f 函数，也就是会往执行栈里一共添加n-1个 f 函数，如果 n很大，不会爆栈吗？

尾递归

当递归调用是整个函数体中最后执行的语句且它的返回值不属于表达式的一部分时，这个递归调用就是尾递归。

我们看递归和尾递归写法区别

//递归
return f(n - 1) + f(n - 2)
//尾递归
return f(n-1,...)

显然，尾递归的返回值不像递归又参与了加法运算

编译器会利用这种特点自动生成优化的代码，编译器会用f(n-1)直接覆盖f(n)，而不是再在栈中创建新的函数，显然这样能大大减少栈空间，所以就不会爆栈了。

总结

递归求斐波那契数列的第n项，时间复杂度O(2^n)，n稍大时计算就很复杂，所以我们从尾部开始算起，通过记录上一次的结果，不断计算。

如果要用递归写法，应改成尾递归形式，时间复杂度O(n)，而且可以利用编译器的优化，极大节省内存

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！