现代密码学实验7 椭圆加密算法ECC的实现
赞赏码 & 联系方式 & 个人闲话
【实验名称】ECC算法
【实验目的】
1、掌握密码学中常用的公钥密码算法ECC的算法原理;
2、掌握ECC的算法流程和实现方法。
【实验原理】
椭圆加密算法(ECC)是一种公钥加密体制,最初由Koblitz和Miller两人于1985年提出,其数学基础是利用椭圆曲线上的有理点构成Abel加法群上椭圆离散对数的计算困难性。
ECC的主要优势是在某些情况下它比其他的方法使用更小的密钥,比如RSA加密算法,提供相当的或更高等级的安全。ECC的另一个优势是可以定义群之间的双线性映射,基于Weil对或是Tate对;双线性映射已经在密码学中发现了大量的应用,例如基于身份的加密。不过一个缺点是加密和解密操作的实现比其他机制花费的时间长。
【实验内容】
实验内容: 完成数据的加密运算和解密运算,输入明文:security,输入密钥:cryption 对ASCII码进行加密和解密。
代码:(代码解释见代码中注释)
#include
#include
#include
using namespace std;class point
{
public:int x;int y;
};
point P[100];
int num = 0;//取模
int my_mod(int a, int p)
{//注意负数情况要加上一个pint i;i = a / p;int re = a - i * p;if (re >= 0){return re;}else{return re + p;}
}//幂次运算,含模运算,防止溢出
int my_pow(int a, int m, int p)
{int result = 1;for (int i = 0; i < m; i++){result = (result*a) % p;}return result;
}//用于求y,并判断平方根是否为整数
int my_sqrt(int s)
{int t;t = (int)sqrt(s);if (t*t == s){return t;}else {return -1;}
}void all_points(int a,int b,int p)
{for (int i = 0; i < p; i++){int s = i * i * i + a * i + b;while (s < 0){s += p;}s = my_mod(s, p);//判断是否为平方剩余//p为23,是奇素数//Euler准则int re = my_pow(s, (p - 1) / 2, p);if (re == 1){//求yint n = 1, y;int f = my_sqrt(s);if (f != -1){y = f;}else {for (; n <= p - 1;){s = s + n * p;f = my_sqrt(s);if (f != -1){y = f;break;}n++;}}y = my_mod(y, p);P[num].x = i;P[num].y = y;num++;if (y != 0){P[num].x = i;P[num].y = (p - y) % p;num++;}}}
}void show()
{for (int i = 0; i < num; i++){cout << P[i].x << " " << P[i].y << endl;}
}//扩展欧几里得法,递归法
int extend(int a, int b, int&x, int&y)
{if (b == 0){x = 1;y = 0;return a;}int r = extend(b, a % b, x, y);int t = x;x = y;y = t - a / b * y;return r;
}//借助递归扩展欧几里得求逆
int inv(int a, int b)
{int x, y;int r = extend(a, b, x, y);if (r != 1){return 0;}x = x % b;if (x < 0){x = x + b;}return x;
}//两点的加法运算
point add(point p1, point p2, int a, int p)
{long t;int flag = 0;int x1 = p1.x;int y1 = p1.y;int x2 = p2.x;int y2 = p2.y;int tx, ty;int x3, y3;if ((x2 == x1) && (y2 == y1)){//相同点if (y1 == 0){flag = 1;}else {t = (3 * x1*x1 + a)*inv(2 * y1, p) % p;}}else {//不同点相加ty = y2 - y1;tx = x2 - x1;while (tx<0){tx = tx + p;}while (ty<0){ty = ty + p;}if (tx == 0 && ty != 0){flag = 1;}else {//点不相等t = ty * inv(tx, p) % p;}}if (flag == 1){//无限点p2.x = -1;p2.y = -1;}else {x3 = (t*t - x1 - x2) % p;y3 = (t*(x1 - x3) - y1) % p;while (x3<0){x3 += p;}while (y3<0){y3 += p;}p2.x = x3;p2.y = y3;}return p2;
}//随机选取一个生成元并计算阶
int jie(point &pp, int a, int p)
{int ii = rand() % num;point P0 = P[ii];point p1, p2;int number = 1;p1.x = P0.x; p2.x = P0.x;p1.y = P0.y; p2.y = P0.y;while (true){p2 = add(p1, p2, a, p);if (p2.x == -1 && p2.y == -1){break;}number++;if (p2.x == p1.x){break;}}pp.x = p1.x;pp.y = p1.y;int n = ++number;return n;
}//素数判断
bool judge(int num)
{bool ret = true;int ubound = sqrt(num) + 1;for (int i = 2; i < ubound; i++){if (num % i == 0){ret = false;break;}}return ret;
}//计算kG
point cal(point G, int k, int a, int p)
{point temp = G;for (int i = 0; i < k - 1; i++){temp = add(temp, G, a, p);}return temp;
}int main()
{srand(time(NULL));int a, b, p;point generator; int n;char SE[10];char CR[10];cout << "请输入椭圆曲线群(a,b,p):";cin >> a >> b >> p;cout << "请输入明文:";cin >> SE;cout << "请输入密钥:";cin >> CR;//计算所有点all_points(a, b, p);//选取生成元,直到阶为素数do{n = jie(generator, a, p);} while (judge(n) == false);cout << endl << "选取生成元(" << generator.x << "," << generator.y << "),阶为:" << n << endl;//选取私钥int ka = int(CR[0]) % (n - 1) + 1;//选取使用的密钥point pa = cal(generator, ka, a, p);//计算公钥cout << "私钥:" << ka << endl;cout << "公钥:(" << pa.x << "," << pa.y << ")" << endl;//加密int k = 0;//随机数kk = rand() % (n - 2) + 1;point C1 = cal(generator, k, a, p);//计算C1//m嵌入到椭圆曲线int t = rand() % num; //选择映射点point Pt = P[t];point P2 = cal(pa, k, a, p);point Pm = add(Pt, P2, a, p);cout << endl << "要发送的密文:" << endl;cout << "kG=(" << C1.x << "," << C1.y << "),pt+kPa=(" << Pm.x << "," << Pm.y << ")";int C[100];cout<<",C = { ";for (int i = 0; i 运行演示:
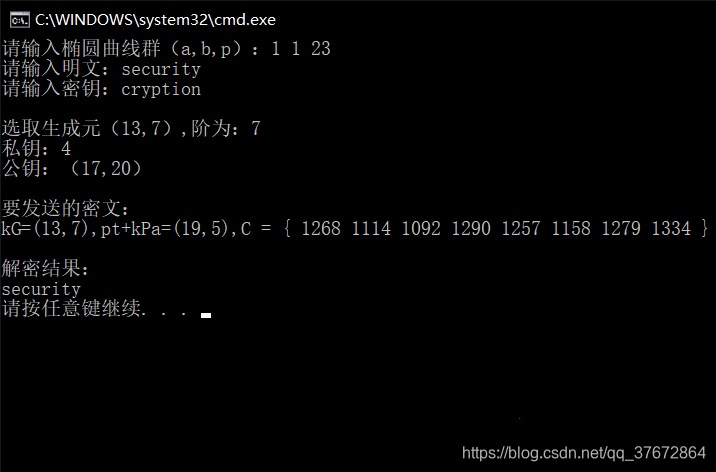
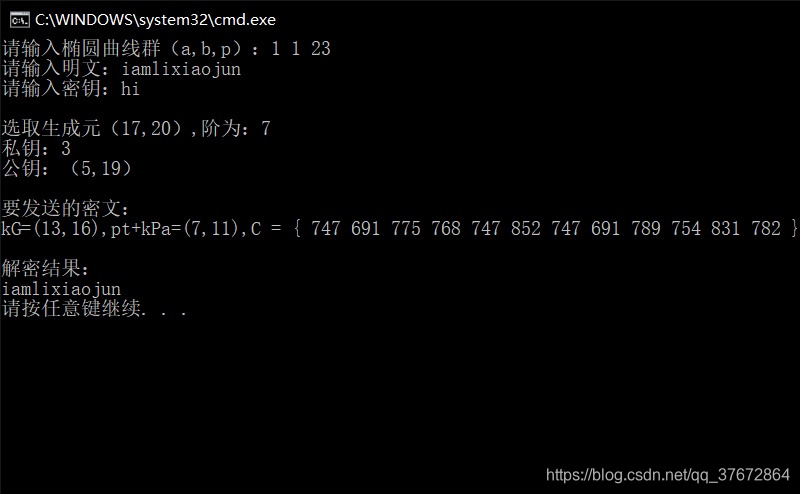
【小结或讨论】
这一次是实验可以说是很有难度的。虽然这个实验和之前的ElGamal算法原理相似,但是其主要是引入了椭圆曲线群。有限域上的椭圆曲线,再加上自己定义的“+”法,其中又涉及到取模、幂次运算、判断平方根、扩展欧几里得法、模数求逆、生成元计算阶、素数判断等等内容,可以说是十分复杂了。
我结合着自己的理解,对算法流程和题目要求做了一些修改,以便更好地实现。由于题目给定的p为23,小了一些,我就不能按照指导书上的流程来完整实现,这不仅是,x取值范围固定为0~22的范围而导致数据无法恢复的问题,还有其可表示的信息太少了,以至于不能表示出26个英文字母的ASCII码值。为了解决这个问题,我结合着网上的一些资料,对把信息m嵌入椭圆曲线的过程做了少许修改,具体实现可以参考上文代码,大概流程就是任意取一个椭圆曲线上的点,C[i] = int(SE[i]) * Pt.x + Pt.y,这样等于隐藏的是我们选择的这一点。解密时通过m = (C[i] - temp1.y) / temp1.x,反向计算即可恢复,这也算是一种信息的嵌入方式。此外,由于给的密文和密钥是英文字符,如果转换成ASCII码我担心计算过程的溢出问题,所以我是拆成一个一个字母处理的,不过这并不影响整个ECC的实现原理和方法。
这一次的实验我感觉有些的综合性,用上了我们之前实验用过的模数求逆、幂次运算、素数判断等,也加上了平方根判断、生成元计算计算等新内容。实验代码虽然不是历次实验最多的,我却觉得是最为复杂的。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!