特征和多项式回归

日萌社

人工智能AI：Keras PyTorch MXNet TensorFlow PaddlePaddle 深度学习实战（不定时更新）

4.特征和多项式回归1.特征选择下面讨论了不单止可以使用两个特征是房子临街宽度frontage和房子纵深长度depth，还可以把两个特征房子临街宽度frontage和房子纵深长度depth两者相乘得到一个特征房子面积大小，上面两个方式都可以应用到线性回归模型，也即可以自由徐选择使用什么特征，并通过设计不同的特征，能够用更复杂的函数拟合数据，而不是只用一条直线去拟合数据。特别是可以使用多项式函数(二次函数/三次函数)去拟合数据。在以后的课程中，会介绍一些算法他们自动会选择要使用什么特征，并且可以让算法观察给出的数据并自动选择使用二次函数/三次函数/其他函数的其中一种。1.如下图中，分别设置有两个特征，分别是房子临街宽度frontage和房子纵深长度depth，然后建立如下的线性回归模型。第一个特征x_1：房子临街宽度frontage。第二个特征x_2：房子纵深长度depth。但当在运用线性回归时，不一定非要直接用给出的特征x_1和特征x_2，也即是可以创造新的特征来使用。比如我要预测房子价格，那么首先需要创造一个房子面积大小的新特征x，也即是房子临街宽度frontage和房子纵深长度depth的乘积，得出公式：房子面积大小(特征x) = 房子临街宽度frontage(特征x_1) * 房子纵深长度depth的乘积个(特征x_2)。2.使用两个特征的线性回归模型：hθ(x)=θ0 + θ1*frontage + θ2*depth第一个特征x_1：房子临街宽度frontage。第二个特征x_2：房子纵深长度depth。3.使用一个特征的线性回归模型：hθ(x)=θ0 + θ1*x唯一一个特征x：房子面积大小(特征x)，他实际是 房子临街宽度frontage(特征x_1) 和 房子纵深长度depth的乘积个(特征x_2) 的乘积。4.此处我们不一定使用两个特征的线性回归模型，也可以转换为使用一个特征的线性回归模型，可能会得到更好的模型。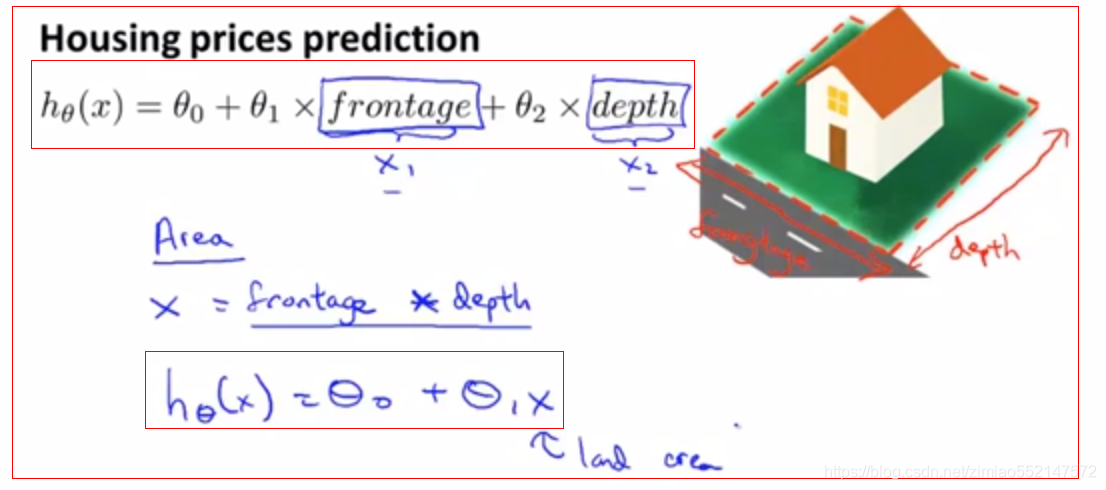

	2.多项式回归多项式回归能够使用线性回归的方法来拟合非常复杂的函数，甚至是非线性函数。下面主要探讨如何将一个多项式(比如二次函数/三次函数)拟合到数据上。1.下图是一个住房价格的数据集，然后还提供有多个不同的公式模型可分别用于拟合数据集。1.第一个公式模型：二次函数模型θ0+θ1*x+θ2*x^2因为直线似乎并不能很好地拟合这些数据，因此可以使用这样的二次函数模型去拟合。考虑到价格可能是一个二次函数，那么便可以画出如下图曲线般去拟合这些数据。但是二次函数模型也存在不合理的地方，比如说二次函数模型最终会降下来，那么就意味着随着房子面积的不断增加达到一个临界点之后，房子面积还继续增加，但是此时的房子价格却不会继续上升，而是开始下降。那么这样的二次函数模型明显并不是我们想要的。

			2.可以选择一个不同的多项式模型，并转而选择使用一个三次函数模型。图中绿色曲线即是三次函数模型的曲线。三次函数模型即使超过了某个临界点，也不会下降，只会继续上升。也即意味着随着房子面积的不断增加，房子价格也继续会上升。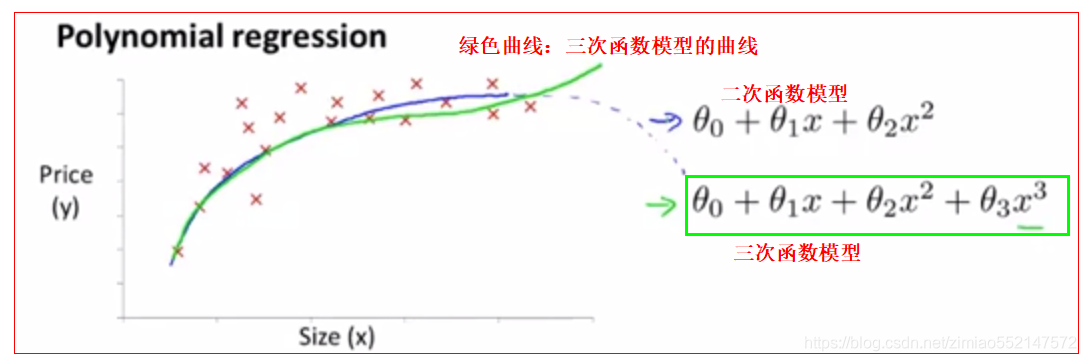

		2.如何使用上述的三次函数模型θ0+θ1*x+θ2*x^2+θ3*x^3与数据集进行拟合1.使用多元线性回归的方法，我们还需要对他进行简单的修改来实现它。按照以前假设函数的形式，那么可以按照下图中般的使用hθ(x)=θ0+θ1*x1+θ2*x2+θ3*x3假设函数来拟合数据。2.下面讨论使用三次函数模型θ0+θ1*x+θ2*x^2+θ3*x^3来拟合数据。例子：下图中要进行预测房子价格。1.θ0+θ1*(size)+θ2*(size)^2+θ3*(size)^3 表示用θ0加θ1乘以房子面积加上θ2乘以房子面积的平方再加上θ3乘以房子面积的立方。2.hθ(x)=θ0+θ1*x1+θ2*x2+θ3*x3 中的x1、x2、x3 均为输入特征。3.要把hθ(x)=θ0+θ1*x1+θ2*x2+θ3*x3 和 θ0+θ1*(size)+θ2*(size)^2+θ3*(size)^3 两者关联起来的话，就需要把特征x1设置为房子面积size，把特征x2设置为房子面积size的平方，把特征x3设置为房子面积size的立方，即设置x1=(size)、x2=(size)^2、x3=(size)^3。然后再运用线性回归方法hθ(x)=θ0+θ1*x1+θ2*x2+θ3*x3，就可以拟合这个三次函数模型θ0+θ1*x+θ2*x^2+θ3*x^3到数据集上。4.如果像上述那样设置特征 x1=(size)、x2=(size)^2、x3=(size)^3的话，那么运用特征缩放就显得更加尤为重要了。特征x1=(size)：房子面积范围大小在1到1000之间特征x2=(size)^2：房子面积的平方的范围大小就在1到一百万(1000的平方)之间特征x3=(size)^3：房子面积的平方的范围大小就在1到10的9次方之间可以看出上述3个特征的范围相差很大，因此如果此时使用梯度下降法的话，那么运用特征缩放就显得更加尤为重要了，因为这样才能控制值的范围变得具有可比性。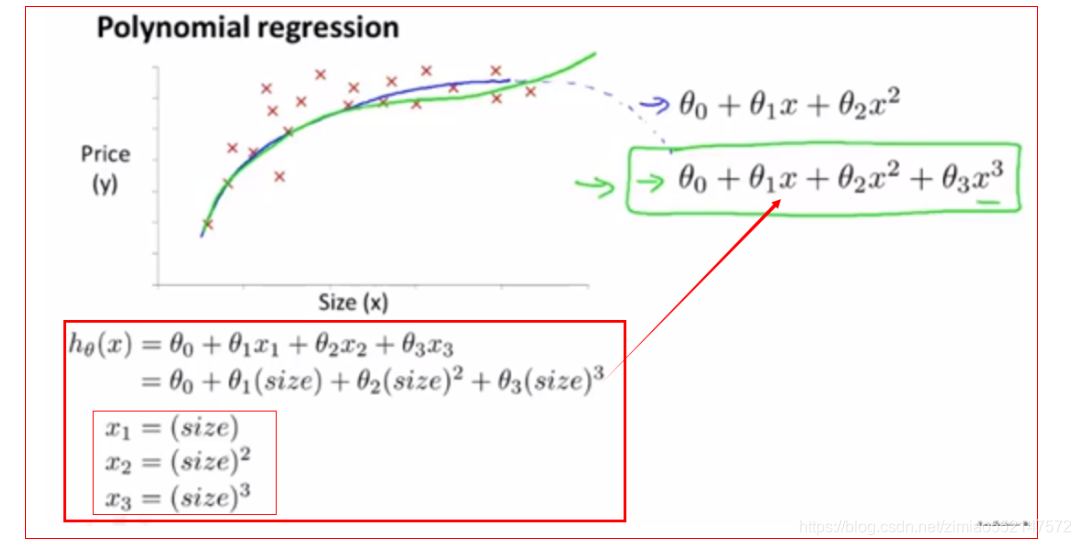

			3.此前所述的二次函数模型θ0+θ1*x+θ2*x^2拟合数据并不是很理想，因为二次函数模型拟合数据到最终曲线会下降，曲线会下降即意味着房子面积增加的情况下房子价格反而下降的情况，这是我们认为该二次函数模型不理想的地方。因此后面我们便改为采用了三次函数模型θ0+θ1*x+θ2*x^2+θ3*x^3来拟合数据。除了使用三次函数模型之外，下图还介绍其他可选的特征所构成合理选择的例子。另外一种合理选择是：hθ(x)=θ0+θ1*(size)+θ2*√￣(size)。√￣(size)表示求房子面积size的平方根。上述公式表示预测的房子价格为θ0加θ1乘以房子面积加θ2乘以房子面积的平方根。那么该函数的曲线是如下图的趋势上升但上升到一定程度之后便慢慢变得平缓，曲线最终也不会下降的，最多也只会缓慢上升。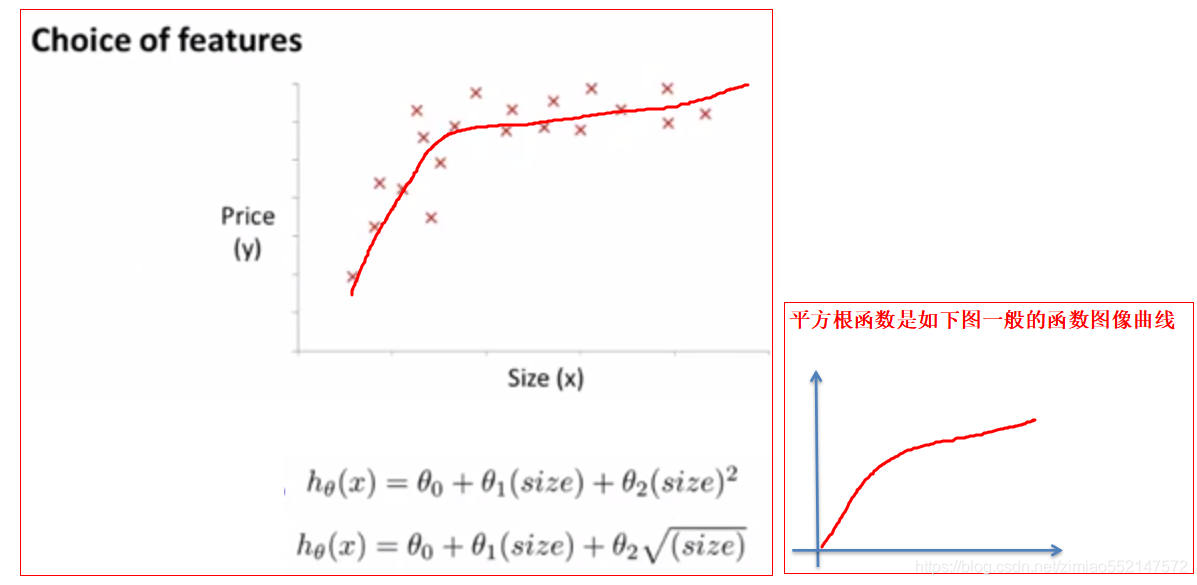

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！