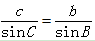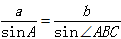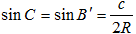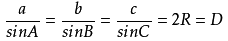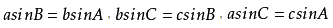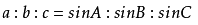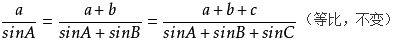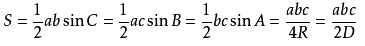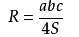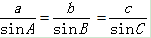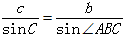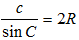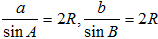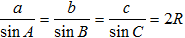1、余弦定理
如下图所示,在△ABC中,余弦定理可表示为:
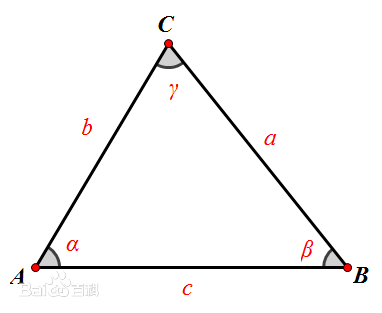

余弦定理的三个证明
转自:http://www.matrix67.com/blog/archives/2324
证明1:
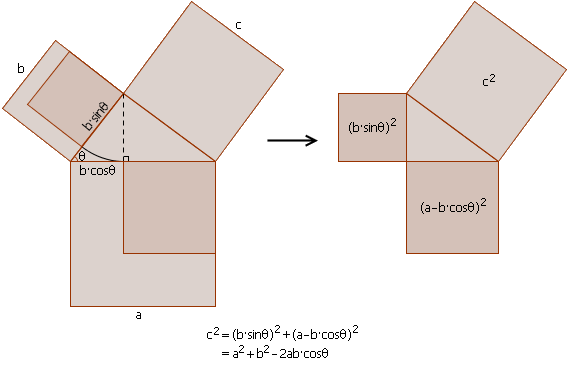
证明2:
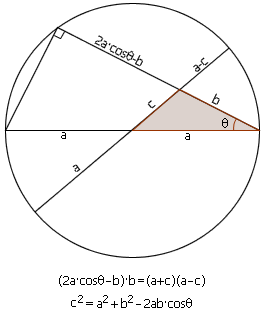
证明三
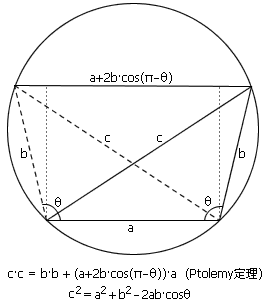
2、正弦定理
在任意△ABC中,角A、B、C所对的边长分别为a、b、c,三角形外接圆的半径为R
则有
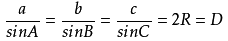
公式变形
△ABC中,若角A,B,C所对的边为a,b,c,三角形外接圆半径为R,直径为D,正弦定理进行变形有
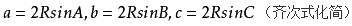
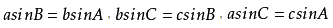
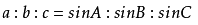
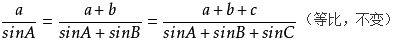
三角形面积公式:
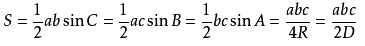
外接圆半径公式: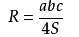
定理证明
前三项的证明
利用三角形的高证明
当△ABC是锐角三角形时,设边 AB 上的高是 CD ,CD = a * sinB,CD = b * sinA
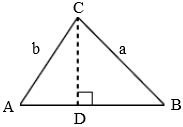
由此,得
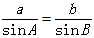
,同理可得
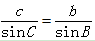
故有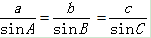
当△ABC是钝角三角形时,过点 C 做 AB 边上的高,交 AB 的延长线于点 D,CD = a * sin∠CBD = a * sin∠ABC ,CD = b * sinA
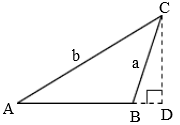
由此,得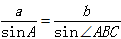 ,同理可得
,同理可得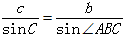
故有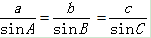
外接圆证明正弦定理
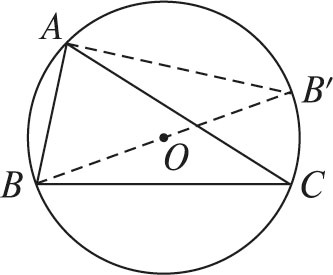
在△ABC中,已知 BC = a,AC = b,AB = c,做三角形 ABC 的外接圆,O 为圆心
连接 BO并延长交圆于 B' ,BB' = 2 * R
根据直径所对的的圆周角是直角以及同弧所对的圆周角相等可以得到 ∠BAB' = 90°,∠C = ∠B',
所以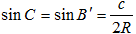 ,
,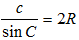
同理可得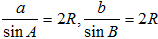
所以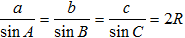
HDU 1374 The Circumference of the Circle
题意:
给出三角形三个顶点的坐标,求外接圆的周长
解题思路:
p = (a + b + c) / 2.0
S = sqrt(p * (p - a) * (p - b) * (p - c))
外接圆直径 D = (a * b * c) / (2.0 * S)
周长 = PI * D
#include
#include
#include
#include
#include
#include
#include
#include
#include
CodeForces_1C Ancient Berland Circus
参考:http://blog.csdn.net/aholic/article/details/21733777
题意:
给出正多边形上的三个点的坐标,,求这个正多边形的最小的面积
解题思路:
由于是确定是正多边形,所以一定存在外接圆
所以可以分为如下几步:
海伦公式求面积:
p = (a+b+c) / 2.0
S = sqrt(p * (p - a) * (p - b) * (p - c))
1.求外接圆半径r = abc / 4S
2.由余弦定理求出三个圆心角
(要注意的是,有可能有三个点在同一段半圆弧上,这是第三个圆心角应该用2π - ang1 - ang2, 所以干脆全部都是 ang3 = 2π - ang1 - ang2)
3.求这三个角的最大公约数为 gcd, 那么这就是一个 n = 2π / gcd 的正 n 边形
4.一个小三角形的面积S = 1/2·r * r * sin(gcd)
5.nS即为所求
#include
#include
#include
#include
#include
#include
#include
#include
#include
三、
内心:内角平分线的交点
旁心:外角平分线的交点
外心:垂直平分线的交点
垂心:高的交点
重心:各边中线的交点
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!
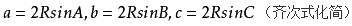

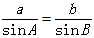 ,同理可得
,同理可得