整理总结：深入浅出统计学——概率计算

参考资料：电子工业出版社的《深入浅出统计学》

前言

内容完全是《概率论》的基础知识，故不展开总结。需要指出的是，概率计算的重点应该根据现有的概率去推算出目标概率值。

本篇目录

• 参考资料：电子工业出版社的《深入浅出统计学》
• • 前言
  • 具体内容
  • • 一、概率
    • 二、条件概率
    • 三、全概率公式
    • 四、贝叶斯公式
    • 五、相交、互斥和独立事件
    • 六、绘图工具
    • • 1、维恩图
      • 2、概率树

具体内容

一、概率

二、条件概率

P ( A ∣ B ) = P ( A ∩ B ) P ( B ) P(A|B)=\frac{P(A \cap B)}{P(B)} P(A∣B)=P(B)P(A∩B)​

三、全概率公式

P ( B ) = P ( A ) × P ( B ∣ A ) + P ( A ′ ) × P ( B ∣ A ′ ) P(B)=P(A) \times P(B|A)+P(A') \times P(B|A') P(B)=P(A)×P(B∣A)+P(A′)×P(B∣A′)

四、贝叶斯公式

P ( A ∣ B ) = P ( A ) × P ( B ∣ A ) P ( A ) × P ( B ∣ A ) + P ( A ′ ) × P ( B ∣ A ′ ) P(A|B)=\frac{P(A) \times P(B|A)}{P(A) \times P(B|A)+P(A') \times P(B|A')} P(A∣B)=P(A)×P(B∣A)+P(A′)×P(B∣A′)P(A)×P(B∣A)​

五、相交、互斥和独立事件

1、相交， P ( x 1 ) + P ( x 2 ) > 1 P(x_1)+P(x_2)>1 P(x1​)+P(x2​)>1。
2、互斥， P ( x 1 ) + P ( x 2 ) = 1 P(x_1)+P(x_2)=1 P(x1​)+P(x2​)=1
3、独立， P ( x 1 ∗ x 2 ) = P ( x 1 ) ∗ P ( x 2 ) P(x_1*x_2)=P(x_1)*P(x_2) P(x1​∗x2​)=P(x1​)∗P(x2​)。

六、绘图工具

1、维恩图

主要用于指出基本概率及各种关系。

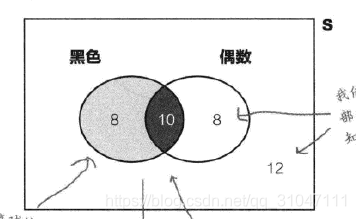
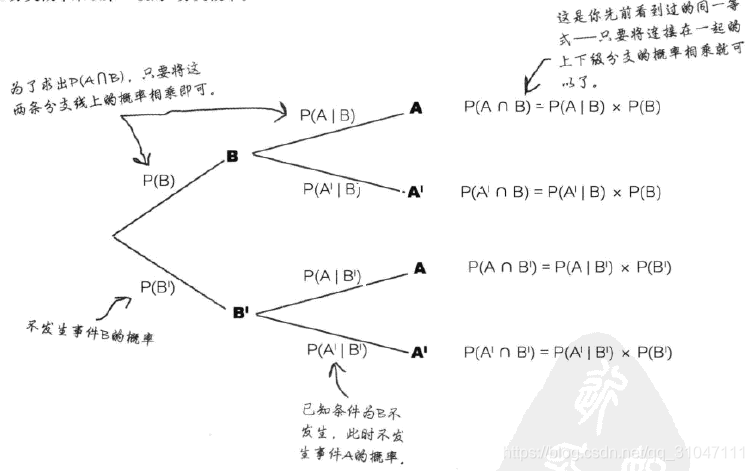
2、概率树

主要用于条件概率的计算。当忘了条件概率的公式时，通过勾画概率树也能轻松地解决。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！