两平面平行方向向量关系_立体几何平行证明的四大必杀绝技------赞!很赞!!非常赞!!!...

类型一:
根据已有平行关系证平行
例题1:已知四棱锥P-ABCD,且G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,且有BC∥平面GEFH,证明GH∥EF。
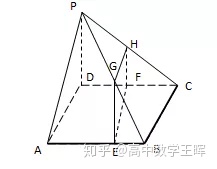
证明:
∵BC∥平面GEFH,
平面GEFH∩平面ABCD=EF且BC⊂平面ABCD
∴BC∥EF
∵EF⊄平面PBC,BC⊂平面PBC
∴平面EF∥平面PBC
∵平面EFGH∩平面PBC=GH
∴EF∥GH
例题2:如图,三棱台DEF-ABC,AB=2DE,且G,H分别为AC,BC的中点,求证:BD∥平面FGH。
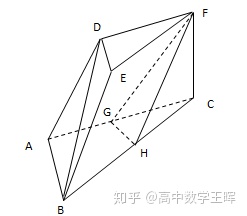
证明:
在三棱台DEF-ABC中,AB=2DE
且H为BC的中点,
∴BH∥EF,且BH=EF
∴四边形BHEF是平行四边形
又G是AC中点,H为BC的中点,根据三角形中位线可得:GH∥AB,又GH∩HF=H
∴平面FGH∥平面ABED
∵BD⊂平面ABED
∴BD∥平面FGH
变式:如图所示,在三棱锥P-ABQ中, D,C,E,F分别是AQ,BQ,AP,BP的中点, PD与EQ交于点G,PC与FQ交于点H,连接GH,求证AB∥GH。
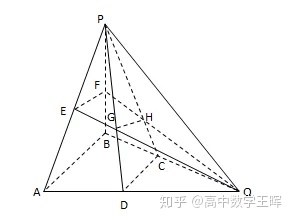
类型二:
利用三角形的中位线证平行
例题:如图,四棱锥P-ABCD,AD∥BC,且AD=2BC,且E,F分别为线段AD,PC的中点,求证:AP∥平面BEF。
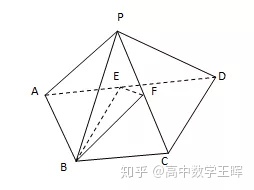
证明:
连接AC,CE,且AC与BE相交于点O,连接OF,如下图:
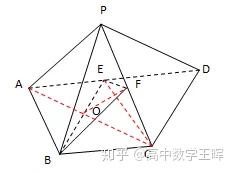
∵AD∥BC,且AD=2BC,且E是AD的中点,
可得:四边形ABCE是平行四边形
∴O是AC的中点,又F是PC的中点
∴OF是△ACP的中位线
∴OF∥PA
∵PA⊄平面BEF,OF⊂平面BEF
∴AP∥平面BEF
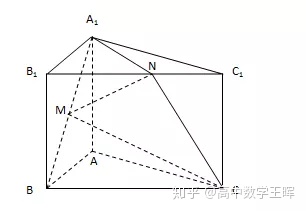
变式:如图,直三棱柱ABC-A1B1C1,点M,N分别为A1B和B1C1的中点,求证:MN∥A1ACC1
类型三:
利用平行四边形的性质证平行
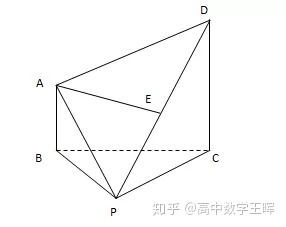
例题1:在四棱锥P-ABCD中,AB∥CD,CD=2AB,E为PD的中点,求证:AE∥平面PBC。
证明:
取PC的中点F,连接EF,BF,如下图:
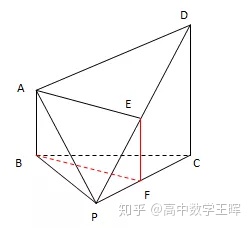
∵E,F分别是PD,PC的中点
∴EF∥CD,且CD=2EF
又AB∥CD,且CD=2AB
∴AB∥EF,且AB=EF即四边形ABFE是平行四边形
∴AE∥BF
又AE⊄平面PBC,BF⊂平面PBC
∴AE∥平面PBC
例题2:如图,三棱柱ABC-A1B1C1中,底面ABC是等边三角形,侧面BCC1B是矩形,AB=A1B,N是B1C的中点,M是棱AA1上的一点,且AA1⊥CM,证明:MN∥ABC
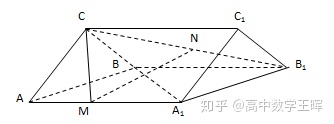
证明:
连接BM,取BC得中点P,连接AP,NP,如下图:
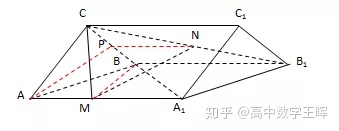
∵BCC1B1是矩形,
∴BC⊥BB1,
∵AA1∥BB1
∴AA1⊥BC
∵AA1⊥MC,BC∩MC=C,
∴AA1⊥平面BCM
∴AA1⊥MB
∵AB=A1B
∴M是AA1的中点,
又P,N分别是CB,CB1的中点,
由三角形的中位线可得:NP∥BB1,且BB1=2NP
∴NP∥MA,且NP=MA
∴四边形AMNP是平行四边形
∴MN∥AP∵MN⊄平面ABC,AP⊂平面ABC
∴MN∥平面ABC
变式:如图,四棱锥P-ABCD,PA⊥底面ABCD,AD∥BC,AD=3,BC=4,且M为线段AD上一点,AM=2MD,N为PC的中点,证明:MN∥平面PAB。
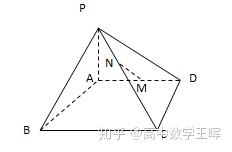
类型四:
利用向量法证平行
1.利用平面法向量
利用法向量证明直线与平面平行的基本原理为:
若平面外一条直线的方向向量垂直于此平面的法向量,则该向量与此平面平行。即若法向量n⊥平面ɑ,且法向量n⊥向量a,则向量a∥平面ɑ
例题:如图,直四棱柱ABCD-A1B1C1D1的底面是正方形,AA1=4,AB=2,E,M,N分别是BC,BB1,A1D的中点,证明:MN∥C1DE
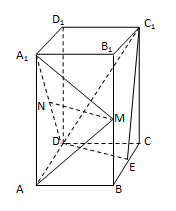
证明:
以D为原点,以DA所在直线为x轴,DC所在直线为y轴,DD1所在直线为z轴,建立空间直角坐标系如下:
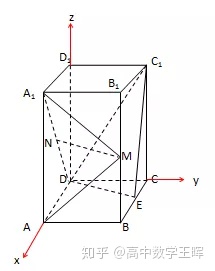
根据AA1=4,AB=2,
可得点的坐标如下:
D(0,0,0),E(1,2,0),C1(0,2,4)M(2,2,2),N(1,0,2)
则有:

2.利用向量共面定理
向量共面定理:
已知向量a,向量b,向量c两两不共线,若存在实数x,y,使得向量c=xa+yb,则向量a,向量b,向量c共面。具体如下动图所示:
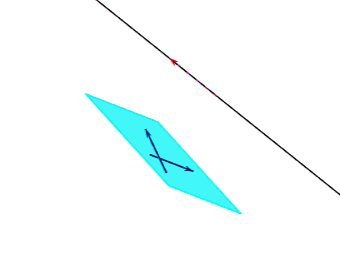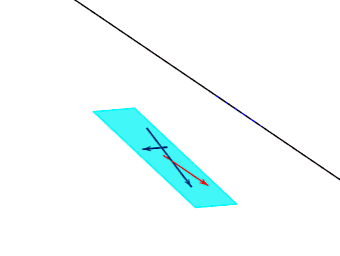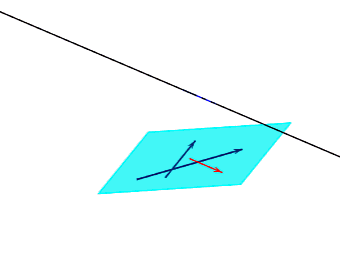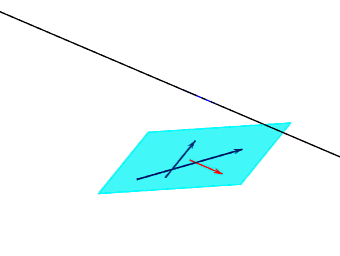
备注:因为向量是可以移动的,所以几个向量共面不代表向量所对应的直线是相互共面的。
例题:如图所示四棱锥P-ABCD中,底面ABCD为正方形,AB=4,PA=2,E为PD的中点,证明:PB∥平面AEC
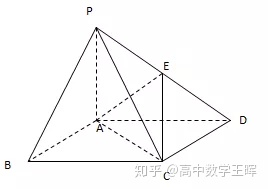
证明:
以A为原点,以AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,建立空间直角坐标系如下:
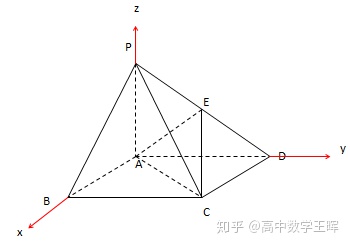
根据AB=4, PA=2,
可得点的坐标如下:
A(0,0,0),P(0,0,2) ,B(4,0,0)D(0,4,0) ,C(4,4,0)
∵E为PD的中点,
∴E(0,2,1)

3.利用平面向量共线定理
平面向量共线定理:
不共线的两条直线所对应的向量分别为向量a,向量b,若向量a=λb,则向量a∥向量b接下来用平面向量共线定理再解上面用法向量求解的例题
例题:如图,直四棱柱ABCD-A1B1C1D1的底面是正方形,AA1=4,AB=2,E,M,N分别是BC,BB1,A1D的中点,证明:MN∥C1DE

证明:
以D为原点,以DA所在直线为x轴,DC所在直线为y轴,DD1所在直线为z轴,建立空间直角坐标系如下:

根据AA1=4,AB=2,
可得点的坐标如下:
D(0,0,0),E(1,2,0)M(2,2,2),N(1,0,2)
则有:

本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!