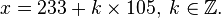算法中那些奇奇妙妙的数学方法

笛卡尔积

通俗点说就是指包含两个集合中任意取出两个元素构成的组合的集合.
例题：不同的二叉搜索树
对于边界情况，当序列长度为 1（只有根）或为 0（空树）时，只有一种情况，即：G(0)=1,G(1)=1
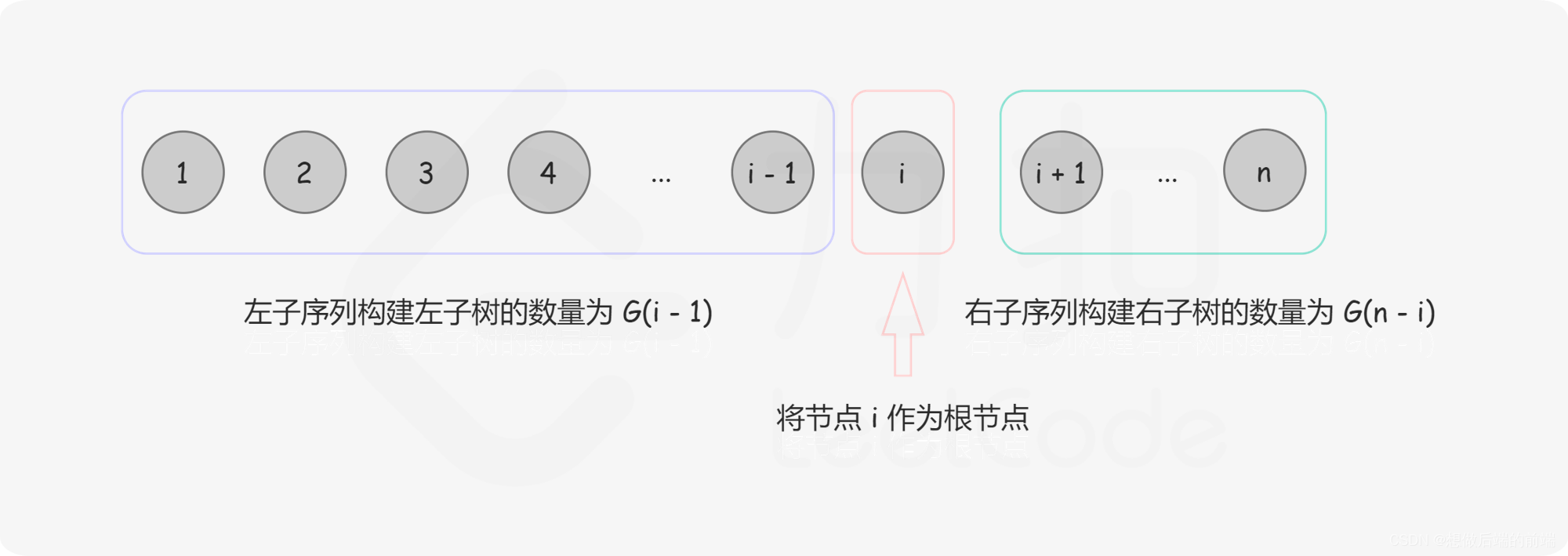
给定序列 1 ⋯n，我们选择数字 ii 作为根，则根为 i 的所有二叉搜索树的集合是左子树集合和右子树集合的笛卡尔积，对于笛卡尔积中的每个元素，加上根节点之后形成完整的二叉搜索树，如下图所示：

class Solution {
public:int numTrees(int n) {vector<int> G(n + 1, 0);G[0] = 1;G[1] = 1;for (int i = 2; i <= n; ++i) {for (int j = 1; j <= i; ++j) {G[i] += G[j - 1] * G[i - j];}}return G[n];}
};

高斯求和公式

给定一个正整数 n，返回 连续正整数满足所有数字之和为 n 的组数 。

class Solution {
public:int consecutiveNumbersSum(int n) {int ans=0;for(int k=1;k*k<=2*n;k++)ans+=(n-(k-1)*k/2)%k==0;return ans;}
};

中国余数定理

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？
即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。一个这样的解为23，所有的解是形如23+105k（k为任意整数）的整数。
《孙子算经》中首次提到了同余方程组问题，以及以上具体问题的解法，因此在中文数学文献中也会将中国剩余定理称为孙子定理。
中国余数定理提出：对于一对两两互质的模数来说，起取模运算的方程组与其对积取模运算的方程之间存在着一种对应关系。

求解方法：

1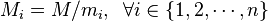）是除了mi以外的n - 1个整数的乘积。

三个模数m1=3, m2=5, m3=7的乘积是M=105，对应的M1=35, M2=21, M3=15.

2）计算出相应的数论倒数：

则求得 t1=2, t2=1, t3=1.

3）

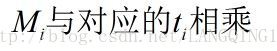
35×2=70 21×1=21 15×1=15

4）3）得到的结果与对应的余数相乘，结果相加

70×2 + 21×3 + 15×2 = 233

5）解的形式

《孙子算经》中实际上给出了最小正整数解，也就是k=-2时的解：x=23.

拒绝采样

给定方法 rand7 可生成 [1,7] 范围内的均匀随机整数，试写一个方法 rand10 生成 [1,10] 范围内的均匀随机整数。

我们可以用拒绝采样的方法实现 Rand10()生成Rand10()。在拒绝采样中，如果生成的随机数满足要求，那么就返回该随机数，否则会不断生成，直到生成一个满足要求的随机数为止。
我们可以调用两次Rand7()，那么可以生成 [1, 49]之间的随机整数，我们只用到其中的前 40 个用来实现Rand10()，而拒绝剩下的 9 个数，如下图所示。

class Solution {
public:int rand10() {int row, col, idx;do {row = rand7();col = rand7();idx = col + (row - 1) * 7;} while (idx > 40);return 1 + (idx - 1) % 10;}
};

三角形面积问题

已知三个点的坐标求面积
由A–>B–>C–>A 按逆时针方向转。(行列式书写要求）
设三角形的面积为S
则S=（1/2)(下面行列式）
|x1 y1 1|
|x2 y2 1|
|x3 y3 1|
S=(1/2)(x1y21+x2y31+x3y11-x1y31-x2y11-x3y21)
即用三角形的三个顶点坐标求其面积的公式为:
S=(1/2)*|(x1y2+x2y3+x3y1-x1y3-x2y1-x3y2)|

凸包算法 - Jarvis Match

Jarvis 算法背后的想法非常简单。我们从给定点集中最左边的点开始，按逆时针方向考虑将所有给定点包围起来的边界点。

这意味着对每一个点 p，我们试图找到一个点 q，满足点 q 是所有点中相对于 p 点逆时针方向最近的点。为了找到点 q，我们使用函数 orientation()，这个函数有 3 个参数，分别是当前凸包上的点 p，下一个会加到凸包里的点 q，其他点空间内的任何一个点 r。如果 q 点相对于 r 点来说在点 p 的逆时针方向上的话，这个函数返回一个负值。
下图说明了这样的关系，点 q 相比点 r 在点 p 的逆时针方向上。

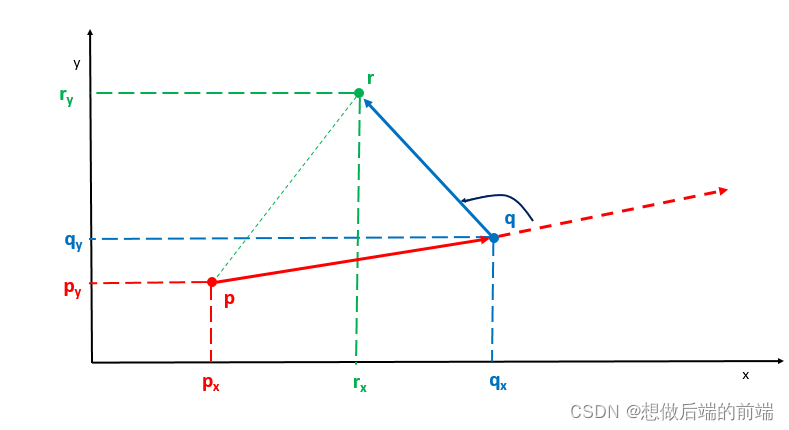
从上图中，我们可以观察到点 p，q 和 r 形成的向量相应地都是逆时针方向，向量 pq和 qr 的方向都朝平面向外，也就是是个正值。

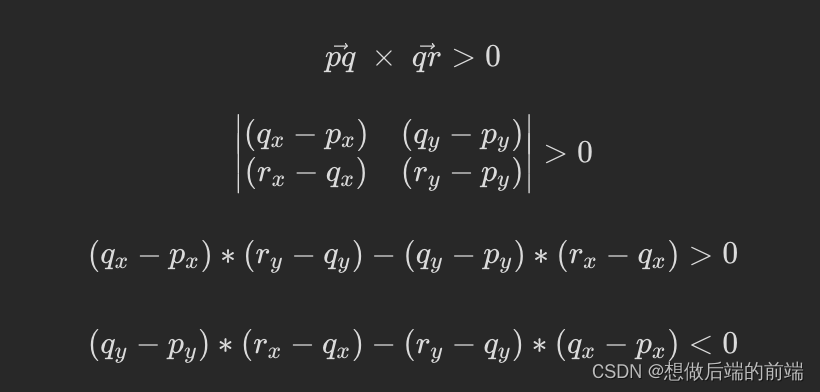
上面的结果通过函数 orientation() 计算。
我们遍历所有点 r，找到相对于点 p 来说逆时针方向最靠外的点 q，把它加入凸包。进一步的，如果存在 2 个点相对点 p 在同一条线上，我们使用 inBetween() 函数，将 q 和 p 同一线段上的边界点都考虑进来。
通过这样，我们不断将凸包上的点加入，直到回到了开始的点。
下面的动图描述了该过程。

import java.util.Arrays;
import java.util.Comparator;
import java.util.Stack;public class Solution {public int[][] outerTrees(int[][] trees) {if (trees.length <= 1) {return trees;}int[] bm = bottomLeft(trees);Arrays.sort(trees, (o1, o2) -> {double diff = orientation(bm, o1, o2) - orientation(bm, o2, o1);if (diff == 0) {return distance(bm, o1) - distance(bm, o2);} else {return diff > 0 ? 1 : -1;}});int i = trees.length - 1;while (i >= 0 && orientation(bm, trees[trees.length - 1], trees[i]) == 0) {i--;}for (int l = i + 1, h = trees.length - 1; l < h; l++, h--) {int[] temp = trees[l];trees[l] = trees[h];trees[h] = temp;}Stack<int[]> stack = new Stack<>();stack.push(trees[0]);stack.push(trees[1]);for (int j = 2; j < trees.length; j++) {int[] top = stack.pop();while (orientation(stack.peek(), top, trees[j]) > 0) {top = stack.pop();}stack.push(top);stack.push(trees[j]);}int[][] res = new int[stack.size()][2];int index = 0;for (int[] tree : stack) {res[index] = tree;index++;}return res;}public int orientation(int[] p, int[] q, int[] r) {return (q[1] - p[1]) * (r[0] - q[0]) - (q[0] - p[0]) * (r[1] - q[1]);}public int distance(int[] p, int[] q) {return (p[0] - q[0]) * (p[0] - q[0]) + (p[1] - q[1]) * (p[1] - q[1]);}private int[] bottomLeft(int[][] points) {int[] bottomLeft = points[0];for (int[] p : points) {if (p[1] < bottomLeft[1]) {bottomLeft = p;}}return bottomLeft;}
}

裴蜀定理

在数论中，裴蜀定理是一个关于最大公约数（或最大公约式）的定理，裴蜀定理得名于法国数学家艾蒂安·裴蜀。

定理内容
若 a,b 是整数,且 gcd ⁡ ( a , b ) = d ，那么对于任意的整数 x , y , a x + b y 都一定是d 的倍数，特别地，一定存在整数 x , y 使 a x + b y = d 成立。

例题
给你一个正整数数组 nums，你需要从中任选一些子集，然后将子集中每一个数乘以一个 任意整数，并求出他们的和。
假如该和结果为 1，那么原数组就是一个「好数组」，则返回 True；否则请返回 False。

class Solution {
public:bool isGoodArray(vector<int>& nums) {int ans = nums[0];for(const auto &e : nums) {ans = gcd(ans, e);}return ans == 1;}
};

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！