常考算法题

背包问题

一、 问题描述：
给定N种物品和一个背包。物品i的重量是wi，其价值为vi，背包的容量为C。问如何选择装入背包中的物品，使得装入背包中物品的总价值最大？
二、 数据输入：
表格一：物品重量与价值
0 1 2 3
Vi（价值） 0 5 8 7
Wi（重量） 0 2 4 3

三、 结果输出：

图一：程序运行结果
四、 算法描述：
首先0-1背包问题具有最有子序列性质。对于每个物品我们可以有两个选择，放或者不放，当有N个物品，就需要进行N次选择，设f[i][v]表示做出第i次选择后，所选物品放入一个容量为v的背包获得的最大价值。现在有两种选择，放或者不放。
1、如果放入第i件物品，则f[i][v] = f[i-1][v-w[i]]+p[i],表示，前i-1次选择后所选物品放入容量为v-w[i]的背包所获得最大价值为f[i-1][v-w[i]]，加上当前所选的第i个物品的价值p[i]即为f[i][v]。
2、果不放入第i件物品，则有f[i][v] = f[i-1][v],表示当不选第i件物品时，f[i][v]就转化为前i-1次选择后所选物品占容量为v时的最大价值f[i-1][v]。既:
f[i][v] = max{f[i-1][v], f[i-1][v-wi[i]]+vi[i]}

五、 算法设计：
使用动态规划的方法
根据上述算法描述，我们需要循环N次，再循环的过程中就会存在重复的计算，于是我们可以用到动态规划算法，每一次运算时，把之前解出的数据存放起来 ，用到的时候再拿出来，这样就可以减少运行时间，提高运行效率。
六、 举例：
引用表格一：
0 1 2 3
Vi 0 5 8 7
Wi 0 2 4 3
当i为1时，首先判断第一个物品的重量是否小于等于背包容量，判断成立，当前背包的价值为5，当前背包容量为3，背包容量大于0，继续放入；当i为2时，判断第二个物品的重量是否小于等于背包容量，判断不行，此时背包的价值为5；当i为3时，判断第三个物品的重量是否小于等于背包容量，判断成立，此时背包的价值为5+7=12，当前背包容量为0；循环结束，找到最大价值。
本问题主要是判断书包能否装下，当找到第i位不能装下时，此时的最大价值就是i-1的位置，当第i为可以放下，就需要第i位的总价值与第i-1位的总价值相比较，放入总价最大的。
程序：
class Main {
public static void main(String[] args) {
int[] w = {5，6，3，7，8};
int[] v = { 6，7，4，8，9 };
int N = 6, W = 21;
int[][] b = new int[N][W];
for (int k = 1; k < N; k++) {
for (int c = 1; c < W; c++) {
if (w[k] > c) {
b[k][c] = b[k - 1][c];
} else {
int value1 = b[k - 1][c - w[k]] + v[k]; // 拿第k件物品
int value2 = b[k - 1][c]; // 不拿第k件物品
b[k][c] = Math.max(value1, value2);
}
}
}
System.out.println(b[5][20]);
}
}

单源最短路径

一、 问题描述：
给定一个带权有向图，且权值都为非负数，给定一个源点，求该点到各个顶点的最短路径。
二、 输入：
0 10 0 30 100
0 0 50 0 0
0 0 0 0 10
0 0 20 0 60
0 0 0 0 0
三、 输出：

图一：单源最短路径
四、 算法描述：
首先，设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。初始时，S中仅含有源。设u是G的某一个顶点，把从源到u且中间只经过S中顶点的路径为从源到u的特殊路径，并用数组dist记录当前每个顶点所对应的最短路经长度。找到后，对dist作必要的修改。
五、 算法设计：
使用贪心算法
每一步都寻找最优的解，从顶点不断地向下寻找，不断地更新dist数组。直到数组内的顶点全部找完。
六、 举例：

图二：一个带权有向图
表一：Dijkstra的运算过程
1 2 3 4 5
{1} 0 10 Max 30 100
{1,2} 0 0 60 30 100
{1,2,4} 0 0 50 0 90
{1,2,4,3} 0 0 0 0 60
{1,2,4,3,5} 0 0 0 0 0
首先令点1为顶点，点1可以到达的点将权值存入其中，不能到达的点为无线大，在第一个存入的集合中寻找最小的权值，发现是10，既从点2开始找，发现点2只能到达点3，用12加上23的权值小于max，说明可以更新，既13当前最优权值为60，其余的数不变，更新数组，继续寻找当前数组内最小的权值，发现是30，既顶点4，发现点4可以到达3,5两个点，发现14加上43的权值14加上45的权值小于当前数组中的权值，更新数组，继续寻找当前数组中的最小权值，发现是50，既顶点3，发现点3只能到达点5,13加上35的最小权值小于数组中的权值，更新数组。发现所有的点都已经找完，得到最优的最单路径。
表二：单源最短路径
0 10 50 30 60

七、 附录：
#include
#include

using namespace std;

#define Length 6

void out(int a[])
{
for(int i=1;i cout< cout< }

void dijkstra(int *dist,int m[][Length],bool *s,int u)
{
if(u<1||u>6) //异常输入
return;
int i,j,temp;
for(i=0;i {
dist[i] = 0;
s[i] = false;
}
s[u] = true; //将源点的标志设为true，表示该点已经遍历
temp = 1000; //最大值
dist[u] = temp;
for(i=1;i {
if(!s[i])
{
if(m[u][i]!=0)
dist[i] = m[u][i];
else
dist[i] = temp;
}
}
for(j=1;j {
temp = 1000;
for(i=1;i {
if((!s[i])&&temp>dist[i])
{
temp = dist[i];
u = i;
}
}
s[u] = true;
for(i=1;i {
if(!s[i]&&m[u][i]!=0)
{
int newdist = m[u][i]+dist[u];
if(newdist dist[i] = newdist;
}
}
out(dist);
}
}

int main()
{
int i,j;
int m[Length][Length];
int dist[Length];
bool s[Length];
for(i=1;i for(j=0;j m[i][j] = -1;
for(i=1;i {
for(j=1;j {
cin>>m[i][j];
}
}
dijkstra(dist,m,s,1);
return 0;
}

符号三角形问题

一、 问题描述：
给定n个矩阵{A1，A2，…，An}，其中Ai与Ai+1是可乘的，i=1,2,…,n-1，求矩阵相乘至少需要多少次数乘？
二、 输入：
A1 10100，A2 1005，A3 550
三、输出：

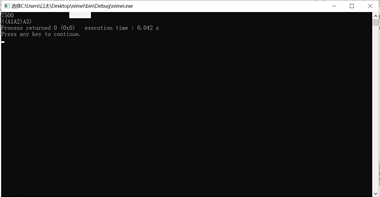
图一为A1A2*A3至少需要的次数乘数值

三、 算法描述：
寻找最优子结构
此问题最难的地方在于找到最优子结构。对乘积A1A2…An的任意加括号方法都会将序列在某个地方分成两部分，也就是最后一次乘法计算的地方，我们将这个位置记为k，也就是说首先计算A1…Ak和Ak+1…An，然后再将这两部分的结果相乘。
最优子结构如下：假设A1A2…An的一个最优加括号把乘积在Ak和Ak+1间分开，则前缀子链A1…Ak的加括号方式必定为A1…Ak的一个最优加括号，后缀子链同理。
一开始并不知道k的确切位置，需要遍历所有位置以保证找到合适的k来分割乘积。
四、 算法设计：
构造递归解
设m[i,j]为矩阵链Ai…Aj的最优解的代价，则
构建辅助表，解决重叠子问题
从第二步的递归式可以发现解的过程中会有很多重叠子问题，可以用一个nXn维的辅助表m[n][n] s[n][n]分别表示最优乘积代价及其分割位置k 。

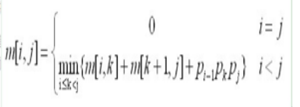
辅助表s[n][n]可以由2种方法构造，一种是自底向上填表构建，该方法要求按照递增的方式逐步填写子问题的解，也就是先计算长度为2的所有矩阵链的解，然后计算长度3的矩阵链，直到长度n；另一种是自顶向下填表的备忘录法，该方法将表的每个元素初始化为某特殊值(本问题中可以将最优乘积代价设置为一极大值)，以表示待计算，在递归的过程中逐个填入遇到的子问题的解。
五、 程序：
#include
using namespace std;

const int N=4;
//p为矩阵链，p[0],p[1]代表第一个矩阵的行数和列数，p[1],p[2]代表第二个矩阵的行数和列数…length为p的长度
//所以如果有六个矩阵，length=7，m为存储最优结果的二维矩阵，s为存储选择最优结果路线的
//二维矩阵
void MatrixChainOrder(int *p,int m[N][N],int s[N][N],int length)
{
int n=length-1;
int l,i,j,k,q=0;
//m[i][i]只有一个矩阵，所以相乘次数为0，即m[i][i]=0;
for(i=1;i {
m[i][i]=0;
}
//l表示矩阵链的长度
// l=2时，计算 m[i,i+1],i=1,2,…,n-1 (长度l=2的链的最小代价)
for(l=2;l<=n;l++)
{
for(i=1;i<=n-l+1;i++)
{
j=i+l-1; //以i为起始位置，j为长度为l的链的末位，
m[i][j]=0x7fffffff;
//k从i到j-1,以k为位置划分
for(k=i;k<=j-1;k++)
{
q=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(q {
m[i][j]=q;
s[i][j]=k;
}
}
}
}
cout << m[1][N-1] << endl;
}
void PrintAnswer(int s[N][N],int i,int j)
{
if(i==j)
{
cout<<“A”< }
else
{
cout<<"(";
PrintAnswer(s,i,s[i][j]);
PrintAnswer(s,s[i][j]+1,j);
cout<<")";
}
}
int main()
{
int p[N]={10,100,5,50};
int m[N][N],s[N][N];
MatrixChainOrder(p,m,s,N);
PrintAnswer(s,1,N-1);
return 0;
}

旅行售货员

一、 问题描述：
某售货员要到若干城市去推销商品，已知各城市之间的路程(或旅费)。他要选定一条从驻地出发，经过每个城市一次，最后回到驻地的路线，使总的路程(或总旅费)最小。
二、 输入：
12=21=30 14=41=4 13=31=6
23=32=5 24=42=10 34=43=20
三、 输出：

图一：最优解
四、 算法描述：
旅行售货员问题的解空间是一颗排列树。我们可以假设初始的一条路线为x，x中的值为1，2，3，……，n，表示该路线为由城市1依次经过城市2、3……到n后再回到城市1（当然是假设该路线存在）。我们通过递归实现，在递归的过程中适当地“剪枝”即除去那些不可能形成最优解的解。
五、 算法设计：
使用回溯法
我们先定义约束条件，当我们进行递归搜索，搜索到第t层时，我们需要判断一下x[t]所代表的城市是否与上一层x[t-1]所代表的城市有“路”，如果没有的话，需要改变x[t]的值，然后继续上述判断，当出现一个满足条件的x[t]后还要判断当前从1到t-1所走的路程cc加上x[t]与x[t-1]的距离是否小于当前已经记录的最优值，如果到t的距离比当前最优值还要大的话，那么再以这条路线搜索下去的话回到城市1的路程一定比当前最优值还大，所以我们没有必要对这条路线进行下一步的搜索，放弃这条路。当我们搜索到第n层，既t = n，说明已经搜索到了叶子结点，这个时候我们还需做上述所说的两个判断，如果两个判断都通过的话，说明该解比当前最优值还优，那么我们需要将该解记录下来，并记录该解的最优值。
六、 举例：
20
1 8 2
5 6
12
3 10 4
图二：旅行售货员所走的路程
首先从1城市开始走，有三种选择，分别是2、3、4，当深度为1时，表示为12 3 4、13 24、14 23，现将12 34拿出来，12 34意思是从1到2，后面的3 4还没有确定，当深度为2时，就是123 4或者124 3，当深度为3时，则循环结束，就这样将每一种的路程存起来，取出最优的路程即可。
七、 附录：
#include
using namespace std;

const int MAX = 1000;
int n, cc = 0, bestc = MAX;// 当前费用、当前最优值
int **g;
int *x, *bestx;//当前最优解

void travel(int t)
{
if (t == n)
{
if (g[x[t - 1]][x[t]] != MAX && g[x[t]][1] != MAX &&(cc + g[x[t - 1]][x[t]] + g[x[t]][1] < bestc || bestc == MAX))
{
for (int i = 0; i < n + 1; i++)
bestx[i] = x[i];
bestc = cc + g[x[t - 1]][x[t]] + g[x[t]][1];
}
return;
}
for (int i = t; i < n; i++)
{
if (g[x[t - 1]][x[i]] != MAX && (cc + g[x[t - 1]][x[i]] < bestc|| bestc == MAX))
{
swap(x[i], x[t]);
cc += g[x[t - 1]][x[t]];
travel(t + 1);
cc -= g[x[t - 1]][x[t]];
swap(x[i], x[t]);
}
}
}

void printf()
{
cout << “输出最优的路程:”;
cout << bestc << endl;
cout << “输出的最优顺序:”;
cout << bestx[1];
for (int i = 2; i < n + 1; i++)
cout << " " << bestx[i];
cout << " " << bestx[1] << endl;
}

int main() {
n = 4;
g = new int*[n + 1];
x = new int[n + 1];
bestx = new int[n + 1];
for (int i = 0; i < n + 1; i++) {
g[i] = new int[n + 1];
x[i] = i;

	for (int j = 0; j < n + 1; j++)g[i][j] = MAX;
}
g[1][2] = g[2][1] = 30;
g[1][3] = g[3][1] = 6;
g[1][4] = g[4][1] = 4;
g[2][3] = g[3][2] = 5;
g[2][4] = g[4][2] = 10;
g[3][4] = g[4][3] = 20;
travel(2);
printf();return 0;

}

最优装载

一、 问题描述：
有一批集装箱要装上一艘载重量为c的轮船。其中集装箱i的重量为Wi。最优装载问题要求确定在装载体积不受限制的情况下，将尽可能多的集装箱装上轮船。
二、 输入：
表格一：物品的重量
序号 0 1 2 3 4 5 6 7 8 9
重量 10 15 12 13 14 15 16 17 18 19

三、 输出：

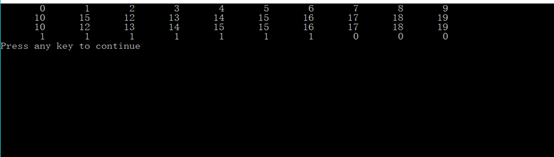
图一：放入轮船的物品
四、 算法描述：
定义存放的重量w[]、总容量为c、定义一个新数组数组内的序号定义为0，首先把数组的序号和数值打印出来，进行冒泡排序，把排序好的数组内的值打印一遍，开始往船上放物品，每放入一个物品，把这个物品的下标定义为1，并且用总容量c-w[i]，当c大于0，就一直存放，直到不能放入为止。
五、 算法设计：
使用贪心算法
首先要明白贪心算法，贪心算法以贪心为主，要达到每一步都是最优解。
于是，我先对物品的重量进行排序，在问题描述中已经得知，要将尽可能多的集装箱装上轮船，所以我按照从小到大的顺序物品排序完毕后，开始往轮船上放；在每一次放入后，刷新剩余的总容量，并将放入物品的下表定义为1，就这样依次装入，直到物品不能放入为止。
六、 举例：

表格二：排序后的物品重量
序号 0 1 2 3 4 5 6 7 8 9
重量 10 12 13 14 15 15 16 17 18 19
0 0 0 0 0 0 0 0 0 0
因为轮船的容量为100，当第一个物品放入后当前背背包的容量为90，并且下标为1.
表格三：第一个物品放入后
序号 0 1 2 3 4 5 6 7 8 9
重量 10 12 13 14 15 15 16 17 18 19
1 0 0 0 0 0 0 0 0 0
当第一个物品放入后容量已经变为90，开始放入第二个物品，放入后当前总量为78，并让第二个物品下标为1。
表格四：第二个物品放入后
序号 0 1 2 3 4 5 6 7 8 9
重量 10 12 13 14 15 15 16 17 18 19
1 1 0 0 0 0 0 0 0 0
第二个物品放入后容量由原来的90变为现在的78，准备放入第三个物品，并让第三个下标为1。
表格五：第三个物品放入后
序号 0 1 2 3 4 5 6 7 8 9
重量 10 12 13 14 15 15 16 17 18 19
1 1 1 0 0 0 0 0 0 0
第三个物品放入后容量由原来的78变为现在的64，准备放入第四个物品，并让第四个下标为1。
表格六：第四个物品放入后
序号 0 1 2 3 4 5 6 7 8 9
重量 10 12 13 14 15 15 16 17 18 19
1 1 1 1 0 0 0 0 0 0
第四个物品放入后容量由原来的64变为现在的49，准备放入第五个物品，并让第五个下标为1。
表格七：第五个物品放入后
序号 0 1 2 3 4 5 6 7 8 9
重量 10 12 13 14 15 15 16 17 18 19
1 1 1 1 1 0 0 0 0 0
第五个物品放入后容量由原来的49变为现在的34，准备放入第六个物品，并让第六个下标为1。
表格八：第六个物品放入后
序号 0 1 2 3 4 5 6 7 8 9
重量 10 12 13 14 15 15 16 17 18 19
1 1 1 1 1 1 0 0 0 0
第六个物品放入后容量由原来的34变为现在的18，准备放入第七物品，并让第七个下标为1。
表格九：第七个物品放入后
序号 0 1 2 3 4 5 6 7 8 9
重量 10 12 13 14 15 15 16 17 18 19
1 1 1 1 1 1 1 0 0 0
第七个物品放入后容量由原来的18变为现在的2，准备放入第八个物品，发现第八个物品无法放入，循环结束。

七、附录：
#include
#include
#include

using namespace std;
void maopao(int b[],int t)
{
for (int i=t-1;i>0;i–)
{
for(int j=0;j {
if(b[j]>b[j+1])
{
int temp=b[j];
b[j]=b[j+1];
b[j+1]=temp;
}
}
}
}
void printf1(int b[])
{
for(int i=0;i<5;i++)
{
cout< }
cout< }
void loading(int *a,int *r,int w,int n)
{
r[0]=1;
w-=a[0];
for (int i=1;i {
if(w-a[i]>=0)
{
w-=a[i];
r[i]=1;
}
}
}
void printf2(int *r,int len){
for (int i=0;i {
cout< }
printf("\n");
}

int main()
{
int w[5]={5,6,7,8,9}; //w数组中存放重量，x数组存放要放入的物体的序号
/* int w[20];
for(int i=1;i<=10;i++)
{
cin>>w[i];
}*/
int x[5];
int dinyi[5]={0};
int c=20;
for(int j = 0;j<5;j++)
{
x[j]=j;
cout< }
cout< printf1(w);
maopao(w,5);
printf1(w);
loading(w,dinyi,c,5);
printf2(dinyi,5);

return 0;

}

活动安排问题

一、 问题描述：
一个给定序列的子序列是在该序列中删去若干元素后得到的序列。当z既是x的子序列又是y的子序列是，称z为x和y的公共子序列。现给定两个序列x和y，求x和y的最长公共子序列的长度。
二、 输入：
x={A,B,C,B,D,A,B}
y={B,D,C,A,B,A}
三、 输出：

图1为x和y的最长公共子序列的长度

四、 算法描述：
一个给定序列的子序列是在该序列中删去若干元素后得到的序列。确切地说，若给定序列X=，则另一序列Z＝是X的子序列是指存在一个严格递增的下标序列,使得对于所有j=1,2,…,k有：Xij=Zj例如，序列z=是序列X=的子序列,相应的递增下标序列为<2,3,5,7>。给定两个序列X和Y，当另一序列Z既是X的子序列又是Y的子序列时，称z是序列x和Y的公共子序列。例如，若x＝和Y＝，则序列是X和Y的一个公共子序列,序列 也是X和Y的一个公共子序列。而且，后者是X和Y的一个最长公共子序列．因为x和Y没有长度大于4的公共子序列。
五、 算法设计：
对于长度，我们用一个基础的线性dp来搞定义 f[i][j] 表示处理了 a 字符串的1~ i 和 b 字符串的 1 ~ j ，最长的公共子序列长度是多少转移方程：如果当前的 a[i] == b[j则多一步这些应该都很好理解，最后的答案就存在：f [ strlen(a+1) ] [ strlen(b+1) ]中，表示处理完 a 字符串和 b 字符串后得到的最长长度现在我们来讲一下如何输出最长的LCS

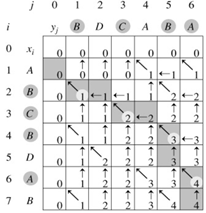
图二为：最长的LCS输出
我们可以在转移的时候记录下，当前状态是由之前的哪一个状态转移而来，最后输出的时候就从后往前递归处理
六、 附录:
#include
using namespace std;

const int n=11;
void GreedySelector(int n, int s[], int f[], bool A[])
{
A[1]=true;
int j=1;
//依次检查活动i是否与当前已选择的活动相容
for(int i=2;i<=n;i++)
{
if (s[i]>=f[j])
{
A[i]=true;
j=i;
}
else
A[i]=false;
}
}

int main()
{
int s[] = {0,1,3,0,5,3,5,6,8,8,2,12};
int f[] = {0,4,5,6,7,8,9,10,11,12,13,14};
bool A[n];
GreedySelector(n, s, f, A);

for(int i = 1; i <= n; i++)     
{  if(A[i]) cout << "活动 " << i << " :" << "(" << s[i] << "," << f[i] << ")" <

}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！