牛顿-莱布尼茨公式是根据变限积分推出来的,当然了如果按照牛顿-莱布尼茨公式来证明变限积分是很容易的事情
如果函数f(x)在区间[a,b]上连续,则积分上限的函数

在[a,b]上可导,则它的导数为
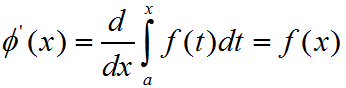
下面给出推论及证明(下面的dΦ(x)都改成dx)
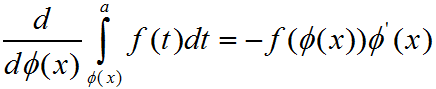

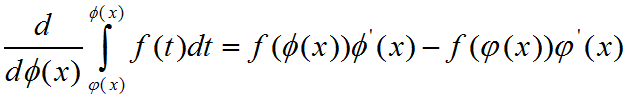


转载于:https://www.cnblogs.com/qinguoyi/p/7605694.html
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!
