C++类:三角函数最小二乘拟合与离散傅里叶变换求解
作为一个天文爱好者,在之前全手工制作了一个天文望远镜导星的系统,但是由于自制的赤道仪使用的是谐波减速器,赤经轴需要一直保持与地球运动同步,每隔一段时间就会有新的谐波齿轮参与啮合,因此造成了在赤经轴存在低频的传动周期误差,该系统利用图像识别观察星点在图像中的偏移可以计算这些误差并下发指令控制赤道仪进行微动调整。赤道仪赤经轴的周期误差基波导致天文望远镜的跟踪误差整体上升了万分之2~5度。在某次测试中,天文望远镜赤道仪的跟踪误差如下图所示(其中红色线是赤经轴的跟踪误差,蓝色是赤纬轴的跟踪误差):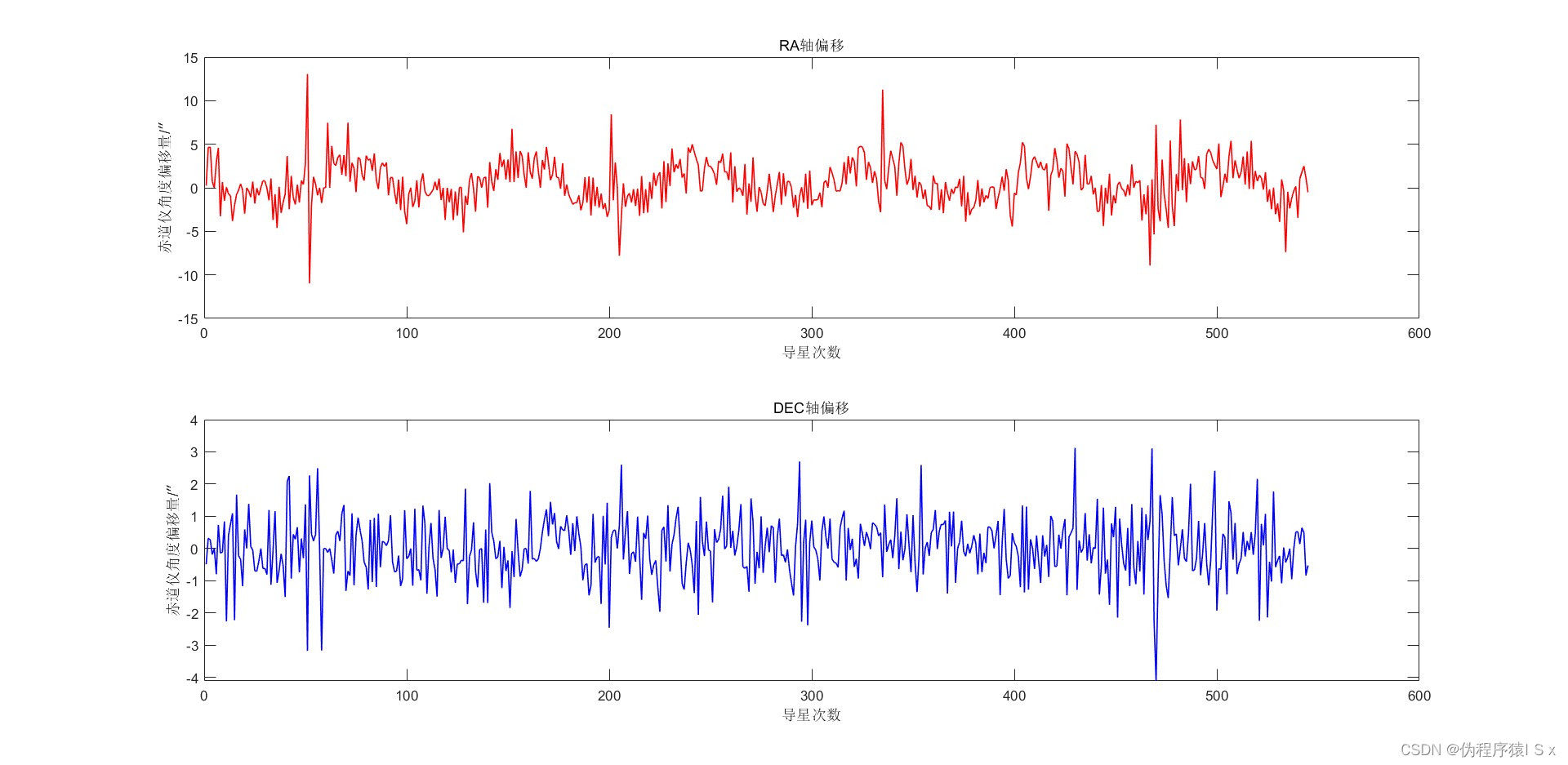 为了解决这个问题,首先利用了离散傅里叶变换(DFT)分析了误差,希望利用傅里叶变换将天文望远镜跟踪误差里面的这个低频周期信号分离出来,得到其幅值、频率和相位,从而在每次跟踪纠正时提前加入这个低频的周期误差的纠正信号,即希望预测这个周期误差的走势,上述信号的傅里叶变换结果如下(图中均为幅频特性,其中红色代表赤经轴跟踪误差的幅频特性,蓝色代表赤纬轴跟踪误差的幅频特性):
为了解决这个问题,首先利用了离散傅里叶变换(DFT)分析了误差,希望利用傅里叶变换将天文望远镜跟踪误差里面的这个低频周期信号分离出来,得到其幅值、频率和相位,从而在每次跟踪纠正时提前加入这个低频的周期误差的纠正信号,即希望预测这个周期误差的走势,上述信号的傅里叶变换结果如下(图中均为幅频特性,其中红色代表赤经轴跟踪误差的幅频特性,蓝色代表赤纬轴跟踪误差的幅频特性):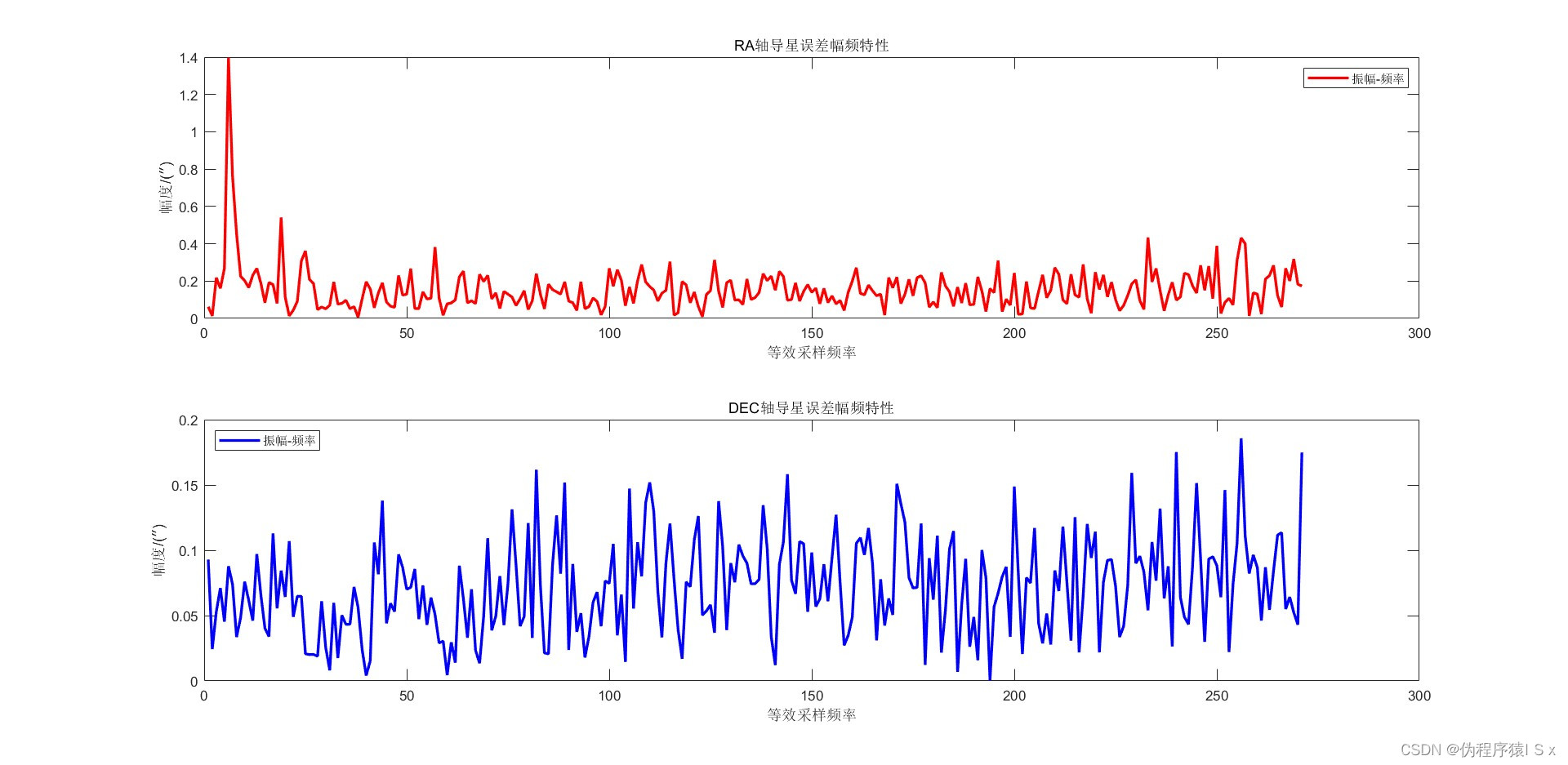
然而傅里叶变换的误差巨大,因为该算法是用于频谱分析的,无法得到一个比较理想的拟合曲线,因此考虑使用最小二乘法拟合这个周期误差。
一、三角函数最小二乘拟合
1 基本公式
首先假设我们得到了一组离散的数据:
于是我们希望通过这N个点找到一个与它们最贴近的一个三角函数:
于是我们计算每个点到这个三角函数的距离:
为了排除负号的影响我们使用距离的平方即:
于是我们可以计算所有数据点到目标三角函数的距离平方之和并将其作为目标函数,即:
将它展开可得:
因而我们的目标是找到最佳的一组参数:
使得目标函数值W最小。
由于三角函数是非线性的,因此为了方便计算,我们首先固定ω,使ω等于一个确定的数ω0,这样就把该目标函数中的三角函数项变成了常数。为了方便以后的讨论,这个条件下的目标函数值表示为:
由于距离的平方满足平方和不等式,因此距离的平方和的和一定存在唯一的最小值,为了求得这个目标函数的唯一最小值,我们对其中的三个变量求偏导数,并令偏导数等于0:
将上述方程展开,将需要的变量A、B、C分离出来,把方程写为矩阵形式:
利用上述矩阵,我们求解出了固定ω时,使得函数F(x)最贴近数据点的参数:
将求出的A、B、C三个参数重新带入原始目标函数就得到了在固定ω=ω0时目标函数的最小值,这里可以将目标函数表示为:
接下来改变ω,通过上述的方法,每次都可以得到一组目标函数的最小值和最小值对应的A、B、C的取值,可以表示为:
最后找到一个最佳的ωbest,使得目标函数的最小值取到最小值:
此时:
这样就求得了最佳的三角函数参数:
这个三角函数的幅值、相位分别为:
2 算法实现以及求解精度优化
2.1 角频率求解区间
该算法主要的问题是需要找到最佳的ωbest,为了准确、保险的找到这个最佳参数,这里建议不要使用任何启发式算法,而对ω进行两次遍历求解即可达到精度要求。首先确定ω可能取值的区间,这个区间如下:
这里:
分别表示输入的待拟合数据点中任意两点之间的横坐标最大值和最小值。其中,k是采样原信号的最小周期数(k<1),例如:如果传感器在最差的情况下只采样了原信号的1/4个周期,则,k = 1/4。设置k以后,输入的原始数据点组成的近似三角函数就应当大于k个周期,如果不清楚采样的数据情况,则k可以置零。
2.2 遍历求解方式
在上述区间中进行第一次遍历求解。若遍历求解的散点个数为N1,即进行N1次遍历求解,假设每次求解的步长相等,则每次遍历求解的步长为:
故ω的取值可以为:
这其中:
假设在上述取值中找到了一个最佳的取值:ωi,则开始进行第二步遍历。此时的角频率取值上下限变为:
假设求解的点数为N2,则ω的取值为:
在这个小区间中找到最佳的一个ωj作为最终的结果即:
2.3 删除不合理数据点
在上述求解中,输入的原始数据中个别数据点可能偏差过大或者不合理,因此这里使用统计学方法扣除这些点,使用3σ准则扣除坏点,定义函数:
其中:
在上述算法输入数据时判断该点的函数值L是否为1,即可选择可信的输入数据。由于在第二阶段遍历求解时ω的变化非常小,扣除坏点的工作可以在第一次求解时进行,而后不再扣除坏点。
总结计算方法:
| STEP1:初步寻找ω | 遍历N1次得到一个最好的ωi,将取值区间的上下界限分别更改为:ωi-1,ωi+1,并得到新的步长 |
| SETP2:精细寻找ω | 在新的极小区间内遍历N2次并且加入误差去除办法,得到最优解ωj |
利用上述算法后拟合得到三角函数结果如下(注:标红的点是算法去除的坏点,红色实线是算法拟合结果):
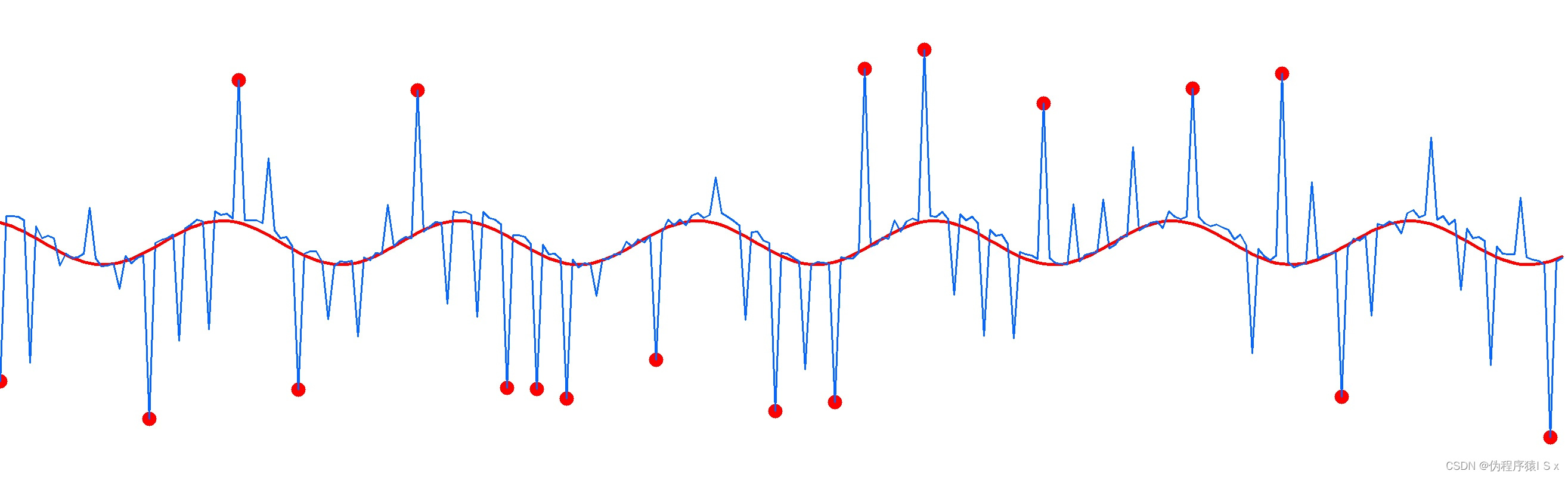
示例代码:
void main()
{int i;double data_1 = 0;double p = 800;double frequncy_ = 20.0;double phase = 0.3;Fourier_transformer This_DFT;while (1) {std::cout << "输入需要预测的时间点:";cin >> p;for (i = 0; i < 263; i++) {data_1 = RANDOM(-1, 1, 0) + 5.0 * cos(Pi / frequncy_ * i + phase);if (i % 5 == 0) {data_1 += RANDOM(-40, 40, 0);}This_DFT.Input_data(data_1, i);}std::cout << "实际:" << 5.0 * cos(Pi / frequncy_ * p + phase)<< std::endl;std::cout << "预测:" << This_DFT.Error_prediction_use_trigonometric_function_fit(p) << std::endl;This_DFT.show_fit_result();This_DFT.reset_retain_predictive_ability();}
}二、离散傅里叶变换(DFT)
若想要了解更加详细的内容,读者可以参考其他博文,这里仅对其计算方法进行简述。
基本公式
假设我们得到了一组时域信号的离散数据,记为:
于是离散傅里叶变换的算法步骤为:
STEP1:提取实部和虚部
STEP2:计算幅值和相位
于是得到了原信号在1~k种情况下的频率和相位,相当于利用不同频率的谐波信号对原信号进行了采样。
利用上述算法后的结果如下(注:其中红线为幅频曲线,蓝线为相频曲线):
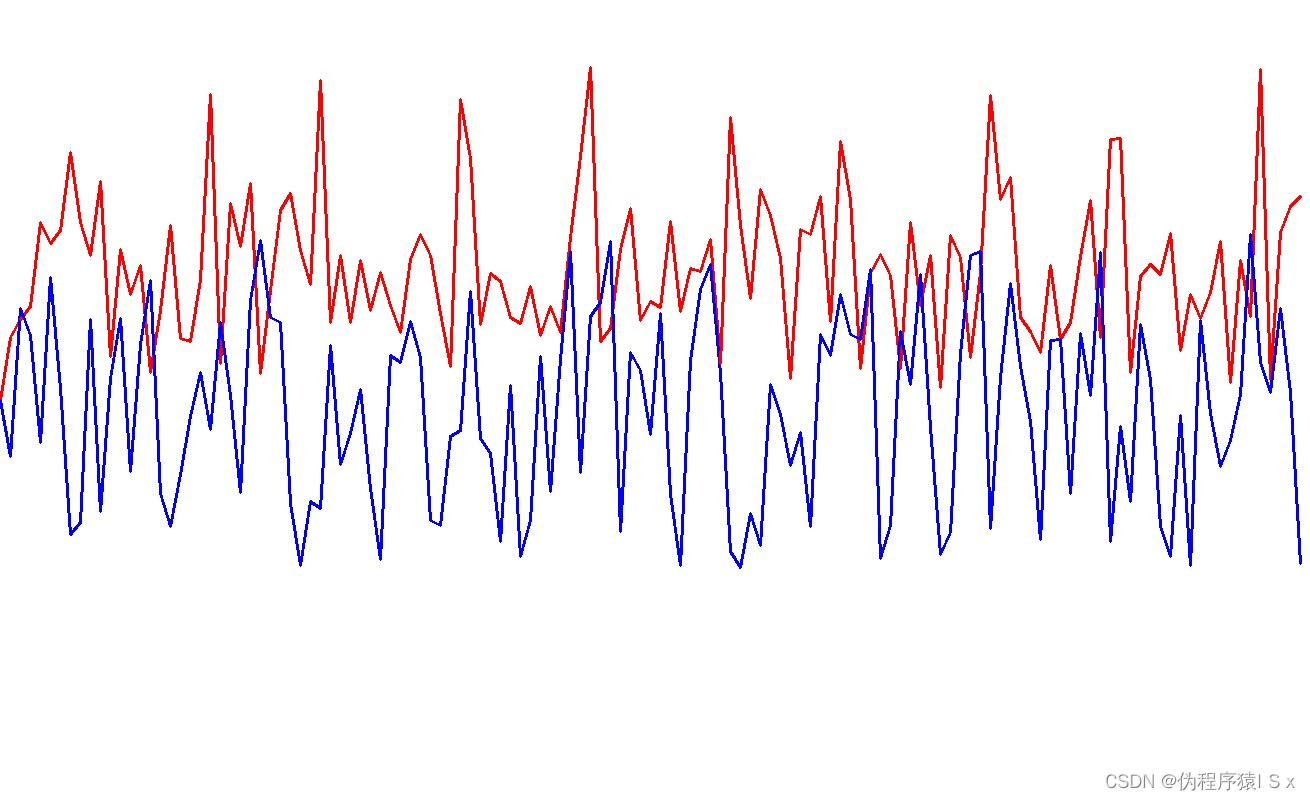
示例代码:
void main()
{int i;double data_1 = 0;double p = 800;double frequncy_ = 20.0;double phase = 0.3;Fourier_transformer This_DFT;while (1) {std::cout << "输入需要预测的时间点:";cin >> p;for (i = 0; i < 263; i++) {data_1 = RANDOM(-1, 1, 0) + 5.0 * cos(Pi / frequncy_ * i + phase);if (i % 5 == 0) {data_1 += RANDOM(-40, 40, 0);}This_DFT.Input_data(data_1, i);}This_DFT.Solve_();This_DFT.show_frequency_domian();}
}三、函数使用
| 函数名称 | 功能 |
| Input_data() | 向类中输入数据 |
| reset_retain_predictive_ability() | 清空类中的数据,但是保留三角函数拟合结果 |
| show_frequency_domian() | 傅里叶变换求解时显示求解结果 |
| show_original_data() | 显示输入的数据(用Opencv绘图) |
| show_fit_result() | 显示三角函数拟合结果 |
| Error_prediction_use_DFT() | 用傅里叶变换预测误差(不建议使用) |
| Error_prediction_use_trigonometric_function_fit() | 使用三角函数最小二乘拟合并预测误差(建议使用) |
| Solve_() | 傅里叶变换求解 |
| Solve_fit() | 三角函数拟合求解 |
| close_display_window() | 关闭显示窗口 |
| printf_data() | 显示傅里叶变换求解结果,打印分离出的谐波的幅值和相位 |
| no_prediction_power() | 判断该类是否有预测能力(调用Solve_fit()求解之后就具有预测能力) |
| printf_fit_harmonic() | 显示三角函数拟合结果 |
附上代码,使用C++编写,三角函数拟合和傅里叶变换放在了一个类里面,该类中还有一个粒子群算法类,可以求解单变量函数的最小值,但是精度不高。
Fourier_transformer.h
#pragma once
#include
#include
#include
#include#define Pi 3.14159265358979324#define SHOW_AMPLITUDE 1#define SHOW_PHASE 2#define SHOW_AMPLITUDE_PHASE 3#define SHOW_TRIGONOMETRIC_FIT 4#define CLOSE_RESULT_WINDOW 1#define CLOSE_ORIGIN_DATA_WINDOW 2#define CLOSE_RESULT_ORIGIN 3#define FIT_DEDUCTING_ERROR_POINT 1#define FIT_NORMAL 2struct sort_partical_self {double position;double value;
};
/*粒子类*/
class one_partical {
public:std::vector self_history;//粒子的历史double V = 0;//粒子速度double position = 0;//粒子位置double now_value = 0;//粒子对应函数值double self_best_position = 1;//粒子最佳函数取值对应的最佳位置double self_best_value = 5000;//粒子最佳函数取值double get_self_best_and_update_best();double set_position(double input_position) {position = input_position;}/*更新速度*/double set_v(double input_v) {V = input_v;}void historey_update(double position, double value) {sort_partical_self Input_;Input_.position = position;Input_.value = value;self_history.push_back(Input_);}
};
/*粒子群类*/
class partical_swarm {
public:/*放置初始位置的粒子*/void put_particals_in_region(double Lower, double Upper);/*设置粒子数目*/void set_patical_number(int input_partical_number);/*设置迭代参数*/void set_parameters(int input_partical_number = 20, int input_max_iteration = 100, double input_omiga_begin = 0.9, double input_omiga_end = 0.4, double input_self_index = 2.0, double input_social_index = 2.5);/*迭代*/void calc_and_update(double(*value_function)(double));double get_best_parameter() {return best_position;}partical_swarm();partical_swarm(int input_patical_number, int input_max_iteration);~partical_swarm() {}
private:std::vector Particals;std::vector global_value_vector;//所有粒子的位置和函数值int iteration_count = 0;//迭代次数int max_iteration_number = 10;//最大迭代次数int patical_number = 0;double lower_ = 0;double upper_ = 0;double omiga_begin = 0.9;double omiga_end = 0.4;double self_index = 2.0;double social_index = 2.0;double global_best_value = 9999999;double global_best_position = 0;double best_value = 9999999999;double best_position = 0;double get_omiga(int input_iteration_count) {return (omiga_begin - omiga_end) * (double(max_iteration_number) - double(input_iteration_count)) + omiga_end;}void update_global_best();
};
/*三角函数参数类*/
struct trigonometric_function_paramater {double A = 0;//系数Adouble B = 0;//系数Bdouble omiga = 0;//角频率double C = 0;//系数Cdouble error_value = 10000;//目标函数值
};
/*用于排序*/
struct sort_function_value
{double omiga = 0;double error_value = 100000;
};
struct function_point {double x = 0;double y = 0;bool is_error_point = FALSE;
};struct to_sort {int position = 0;//位置double amplitude = 0;//幅度double phase = 0;//相位double frequency = 0;
};class Fourier_parameter {
public:int sample_number = 0;std::vector phase;//相位std::vector amplitude;//幅值
private:
};/*傅里叶变换器*/
class Fourier_transformer {
public:/** @brief 输入数据@param input_data 输入的数据@param input_time 数据对应的时间位置*/void Input_data(double input_data,double input_time);/*重置但是保留了针对上一次输入的数据的预测能力*/void reset_retain_predictive_ability();/** @brief 显示幅频曲线和相频曲线@param Show_mode 显示模式,可选:SHOW_AMPLITUDE_PHASE,同时显示幅频曲线和相频曲线;SHOW_AMPLITUDE,只显示幅频曲线;SHOW_PHASE,只显示相频曲线@param rows_ 显示图像的行数@param step_ 两个频率之间的间隔*/void show_frequency_domian(int Show_mode = SHOW_AMPLITUDE_PHASE, int rows_ = 800, int step_ = 10);/** @brief 显示原始信号@param rows_ 显示图像的行数@param step_ 两个频率之间的间隔*/void show_original_data(int rows_ = 800, int step_ = 10);/** @brief 显示拟合信号@param rows_ 显示图像的行数@param step_ 两个频率之间的间隔*/void show_fit_result(int rows_ = 800, int step_ = 10);/** @brief 利用傅里叶变换分离出的周期信号得到误差预测结果@param input_time_position 输入的时间@param frequency_number 选择使用前几的谐波分量预测误差@param low_frequency_domain 定义低频段的系数,该函数只对低频段的周期信号进行预测*/double Error_prediction_use_DFT(double input_time_position, int frequency_number = 4, double low_frequency_domain = 0.3);/** @brief 利用傅里叶变换分离出的周期信号得到误差预测结果@param input_time_position 输入的时间*/double Error_prediction_use_trigonometric_function_fit(double input_time_position);/** @brief 离散傅里叶变换求解*/void Solve_();/** @brief 三角函数拟合求解@param exquisite_number 精细寻找步长系数*/void Solve_fit(int exquisite_number = 7000);/** @brief 关闭所有显示窗口*/void close_display_window(int window_choose = CLOSE_RESULT_ORIGIN);/** @brief 打印分离出的谐波分量数据@param show_number 打印前几个分量*/void printf_data(int show_number = 5);/*傅里叶变换暂时没有能力预测*/bool no_prediction_power();Fourier_transformer();
private:int data_number = 0;int data_number_pre = 0;double time_0_position_pre = 0;//初始时刻的时间位置,只能由solve函数赋值bool DFT_HAVE_SOLVE = FALSE;bool fit_parameter_have_solve = FALSE;std::vector fit_funtion_pre;std::vector time_vector;std::vector The_data_in_time;//时域离散数据,位置即坐标std::vector Re_data;//实部std::vector Im_data;//虚部std::vector Amplitude;//幅值std::vector Phase;//相位std::vector frequency_;//频率std::vector sorting;//用于预测排序的容器std::vector Function_Points;//用于拟合的样本点/*得到实部和虚部信息*/void get_Re_Im_data();/*得到频率和相位信息*/void get_A_p();/*得到最大的前n个谐波分量参数*/Fourier_parameter get_harmonic_parameters();double DFT_max(double a, double b);/*求反正切*/double DFT_arctan(double input_value,double eqs_ = 0.00001);/** @brief 固定频率拟合三角函数@param aomiga 输入的角频率@param Fit_mode 拟合模式@param error_domain 误差区间,利用正态分布扣除误差*/trigonometric_function_paramater fit_trigonometric_function_paramater(double aomiga, int Fit_mode = FIT_NORMAL, double error_domain = 3.0);/** @brief 判断三角函数是否为空@param input_parameter 输入的三角函数*/bool fit_funtion_pre_empty(trigonometric_function_paramater input_parameter);/*随机数*/double DFT_random(double a, double b, double precision = 2);/*最小值*/double DFT_min(double a, double b);
}; Fourier_transformer.cpp
#include"Fourier_transformer.h"clock_t start_c, end_c;
std::vector partical_Function_Points;
bool sort_comp(to_sort& S1, to_sort& S2) {return S1.amplitude > S2.amplitude;
}bool function_value_sort_comp(sort_function_value& S1, sort_function_value& S2) {//从小到大排序return S1.error_value < S2.error_value;
}bool one_partical_find_self_best(sort_partical_self& S1, sort_partical_self& S2) {return S1.value < S2.value;
}double random_(double a, double b, double precision = 2) {int OUTPUT = 0;double GAIN = 1;int i = 0;for (i = 0; i < precision; i++) {GAIN = GAIN * 10;}int A = a * GAIN, B = b * GAIN;OUTPUT = (rand() % (B - A + 1)) + A;double OUTPUT2 = 0;OUTPUT2 = OUTPUT;OUTPUT2 = OUTPUT2 / GAIN;return OUTPUT2;
}double partical_fit_trigonometric_function_paramater(double aomiga) {double sc = 0, c2 = 0, s2 = 0, s = 0, c = 0, y = 0, ys = 0, yc = 0, y2 = 0;//需要计算的取值int i = 0;double ti = 0, yi = 0;double value_ = 0, A = 0, B = 0, C = 0;double average = 0, derta = 0;//统计几何参数double number_ = 0;double judge_value = 0;Eigen::MatrixXd A_Matrix(3, 3), B_Matrix(3, 1), a_vector(3, 1);trigonometric_function_paramater output_;double data_number = double(partical_Function_Points.size());for (i = 0; i < partical_Function_Points.size(); i++) {//循环赋值,从fuction points取数据ti = partical_Function_Points[i].x * aomiga;yi = partical_Function_Points[i].y;//std::cout <<"ti"<< Function_Points[i].y << std::endl;sc += sin(ti) * cos(ti);c2 += cos(ti) * cos(ti);s2 += sin(ti) * sin(ti);s += sin(ti);c += cos(ti);y += yi;ys += yi * sin(ti);yc += yi * cos(ti);y2 += yi * yi;}A_Matrix << c2, sc, c,sc, s2, s,c, s, double(data_number);B_Matrix << yc,ys,y;if (A_Matrix.determinant() != 0) {//安全//std::cout << A_Matrix.determinant() << std::endl;a_vector = (A_Matrix.inverse()) * B_Matrix;A = a_vector(0, 0); B = a_vector(1, 0); C = a_vector(2, 0);value_ = y2 + \A * A * c2 + \B * B * s2 + \2.0 * A * B * sc + \2.0 * A * C * c + \2.0 * B * C * s + \double(data_number) * C * C - \2.0 * A * yc - \2.0 * B * ys - \2.0 * C * y;output_.A = A; output_.B = B; output_.C = C; output_.omiga = aomiga; output_.error_value = value_;//std::cout << "1" << std::endl;}else {output_.error_value = 999999999;}//std::cout << output_.error_value << std::endl;return output_.error_value;
}Fourier_transformer::Fourier_transformer() {srand(time(0));//丢随机数
}double Fourier_transformer::DFT_max(double a, double b) {if (a > b)return a;elsereturn b;
}double Fourier_transformer::DFT_min(double a, double b) {if (a <= b)return a;elsereturn b;
}double Fourier_transformer::DFT_arctan(double input_value, double eqs_) {double start = -Pi / 2.0, end = Pi / 2.0, mid = 0;double start_value = 0, end_value = 0, mid_value = 0;double output_ = 0;int i = 0;;if ((tan(start) - input_value) * (tan(end) - input_value) < 0) {while (abs(start - end) > eqs_) {i++;mid = 0.5 * (start + end);mid_value = tan(mid) - input_value;start_value = tan(start) - input_value;end_value = tan(end) - input_value;if (abs(mid_value) < eqs_)break;else if (mid_value * start_value < 0)end = mid;elsestart = mid;if (i > 200)break;}}else {output_ = atan(input_value);return output_;}output_ = 0.5 * (start + end);//std::cout << i << std::endl;return output_;
}void Fourier_transformer::Input_data(double input_data, double input_time) {function_point this_point;The_data_in_time.push_back(input_data);time_vector.push_back(input_time);this_point.x = input_time;this_point.y = input_data;Function_Points.push_back(this_point);data_number++;//输入的数据计数
}void Fourier_transformer::reset_retain_predictive_ability() {data_number = 0;The_data_in_time.clear();Re_data.clear();Im_data.clear();Amplitude.clear();Phase.clear();time_vector.clear();frequency_.clear();Function_Points.clear();DFT_HAVE_SOLVE = FALSE;
}void Fourier_transformer::get_Re_Im_data() {int i, k;double input_value_Re = 0, input_value_Im = 0;for (k = 0; k < data_number; k++) {input_value_Re = 0;input_value_Im = 0;for (i = 0; i < data_number; i++) {input_value_Re += The_data_in_time[i] * cos(2.0 * Pi * double(k) * double(i) / double(data_number));input_value_Im += -The_data_in_time[i] * sin(2.0 * Pi * double(k) * double(i) / double(data_number));}Re_data.push_back(input_value_Re);Im_data.push_back(input_value_Im);frequency_.push_back(2.0 * Pi * double(k) / double(data_number));}
}void Fourier_transformer::get_A_p() {int k;to_sort this_sort;Re_data.clear();Im_data.clear();Amplitude.clear();Phase.clear();sorting.clear();get_Re_Im_data();for (k = 0; k < data_number; k++) {/*遍历求解*/if (Re_data[k] != 0 && Im_data[k] != 0) {Amplitude.push_back(sqrt(Re_data[k] * Re_data[k] + Im_data[k] * Im_data[k]));Phase.push_back(DFT_arctan(Im_data[k] / Re_data[k]));}else {Amplitude.push_back(0.0);Phase.push_back(0.0);}this_sort.position = k;this_sort.amplitude = Amplitude[k];this_sort.phase = Phase[k];this_sort.frequency = 2.0 * Pi * double(k) / double(data_number);sorting.push_back(this_sort);}data_number_pre = data_number;time_0_position_pre = time_vector[0];DFT_HAVE_SOLVE = TRUE;
}void Fourier_transformer::show_frequency_domian(int Show_mode, int rows_,int step_) {if (data_number > 0) {if (DFT_HAVE_SOLVE) {int data_number1 = data_number / 2;cv::Mat show_mat(rows_, data_number1 * step_, CV_8UC3, cv::Scalar(255, 255, 255));cv::Point2d P1;cv::Point2d P2;cv::Point2d P3;cv::Point2d P4;double max_amplitude = *std::max_element(Amplitude.begin(), Amplitude.end());double max_phase = *std::max_element(Phase.begin(), Phase.end());double min_phase = *std::min_element(Phase.begin(), Phase.end());int i, position_after = 0;int base_line;int font_face = cv::FONT_HERSHEY_SIMPLEX;std::string text_A_w = "amplitude - w:";std::string text_P_w = "Phase - w:";max_phase = DFT_max(abs(max_phase), abs(min_phase));max_phase = 2.0 * max_phase;//cv::putText(show_mat,)cv::Size text_1_size = cv::getTextSize(text_A_w, font_face, 1, 1, &base_line);cv::Size text_2_size = cv::getTextSize(text_P_w, font_face, 1, 1, &base_line);if (Show_mode == SHOW_AMPLITUDE || Show_mode == SHOW_AMPLITUDE_PHASE) {cv::putText(show_mat, text_A_w, cv::Point(1, text_1_size.height + 1), font_face, 1, cv::Scalar(0, 0, 0), 2);cv::line(show_mat, cv::Point(text_1_size.width + 1, text_1_size.height / 2), cv::Point(text_1_size.width + 1 + 30, text_1_size.height / 2), cv::Scalar(0, 0, 255), 2);}else if (Show_mode == SHOW_PHASE || Show_mode == SHOW_AMPLITUDE_PHASE) {cv::putText(show_mat, text_P_w, cv::Point(1, text_1_size.height + 8 + text_2_size.height), font_face, 1, cv::Scalar(0, 0, 0), 2);cv::line(show_mat, cv::Point(text_1_size.width + 1, text_1_size.height + text_2_size.height / 2 + 8), cv::Point(text_1_size.width + 1 + 30, text_1_size.height + text_2_size.height / 2 + 8), cv::Scalar(255, 0, 0), 2);}for (i = 0; i < data_number1; i++) {if (i < data_number1 - 1) {position_after = i + 1;P1.x = double(i) * double(step_);P2.x = (double(i) + 1.0) * double(step_);P3.x = P1.x;P4.x = P2.x;P1.y = -Amplitude[i] * double(0.5 * double(rows_)) / (1.2 * max_amplitude) + 0.5 * double(rows_);P2.y = -Amplitude[position_after] * double(0.5 * double(rows_)) / (1.2 * max_amplitude) + 0.5 * double(rows_);P3.y = -Phase[i] * double(0.5 * double(rows_)) / (1.2 * max_phase) + 0.5 * double(rows_);P4.y = -Phase[position_after] * double(0.5 * double(rows_)) / (1.2 * max_phase) + 0.5 * double(rows_);if (Show_mode == SHOW_AMPLITUDE || Show_mode == SHOW_AMPLITUDE_PHASE)cv::line(show_mat, P1, P2, cv::Scalar(0, 0, 255), 2);if (Show_mode == SHOW_PHASE || Show_mode == SHOW_AMPLITUDE_PHASE)cv::line(show_mat, P3, P4, cv::Scalar(255, 0, 0), 2);}}cv::namedWindow("DFT result", cv::WINDOW_NORMAL);cv::resizeWindow("DFT result", cv::Size(1100, 400));cv::imshow("DFT result", show_mat);cv::waitKey(5);}else {std::cout << "数据未求解!" << std::endl;}}else {std::cout << "未输入数据!" << std::endl;}
}void Fourier_transformer::show_original_data(int rows_, int step_) {if (data_number > 0) {cv::Mat show_mat(rows_, data_number * step_, CV_8UC3, cv::Scalar(255, 255, 255));cv::Point2d P1, P2;int i, i2;double max_data = *std::max_element(The_data_in_time.begin(), The_data_in_time.end());double min_data = *std::min_element(The_data_in_time.begin(), The_data_in_time.end());max_data = DFT_max(abs(max_data), abs(min_data));for (i = 0; i < data_number; i++) {if (i < data_number - 1) {i2 = i + 1;P1.x = double(i) * double(step_);P2.x = double(i2) * double(step_);P1.y = -The_data_in_time[i] * double(0.5 * double(rows_)) / (1.2 * max_data) + 0.5 * double(rows_);P2.y = -The_data_in_time[i2] * double(0.5 * double(rows_)) / (1.2 * max_data) + 0.5 * double(rows_);;}cv::line(show_mat, P1, P2, cv::Scalar(8, 102, 5), 2);}cv::namedWindow("DFT input data", cv::WINDOW_NORMAL);cv::resizeWindow("DFT input data", cv::Size(1100, 400));cv::imshow("DFT input data", show_mat);cv::waitKey(5);}else {std::cout << "未输入数据!" << std::endl;}
}Fourier_parameter Fourier_transformer::get_harmonic_parameters() {Fourier_parameter output_;get_A_p();output_.sample_number = data_number;output_.phase = Phase;output_.amplitude = Amplitude;return output_;
}double Fourier_transformer::Error_prediction_use_DFT(double input_time_position,int frequency_number,double low_frequency_domain) {double output_ = 0;int i;if (!no_prediction_power()) {std::vector sort_stay1 = sorting;//sorting只能由solve函数赋值std::vector::const_iterator first_ = sort_stay1.begin();std::vector::const_iterator end_ = sort_stay1.begin() + ceil(double(data_number_pre) / 2.0);//data_number_pre只能由solve函数赋值std::vector sort_stay(first_, end_);std::sort(sort_stay.begin(), sort_stay.end(), sort_comp);//排序//std::cout << data_number << std::endl;if (frequency_number == -1) {frequency_number = ceil(double(data_number_pre) / 2.0);}for (i = 0; i < frequency_number; i++) {if (sort_stay[i].amplitude <= 0 || sort_stay[i].frequency > 2.0 * Pi * low_frequency_domain)//只要低频段的数据continue;output_ += (sort_stay[i].amplitude * 2.0 / double(data_number_pre)) * cos(sort_stay[i].frequency * (double(input_time_position) - double(time_0_position_pre + 2)) + sort_stay[i].phase);//std::cout << sort_stay[i].phase << std::endl;}}return output_;
}void Fourier_transformer::Solve_() {get_A_p();
}void Fourier_transformer::close_display_window(int window_choose) {if(window_choose == CLOSE_RESULT_WINDOW)cv::destroyWindow("DFT result");if(window_choose == CLOSE_ORIGIN_DATA_WINDOW)cv::destroyWindow("DFT input data");if (window_choose == CLOSE_RESULT_ORIGIN) {cv::destroyWindow("DFT result");cv::destroyWindow("DFT input data");}
}void Fourier_transformer::printf_data(int show_number) {int i;if (DFT_HAVE_SOLVE) {std::vector sort_stay1 = sorting;std::vector::const_iterator first_ = sort_stay1.begin();std::vector::const_iterator end_ = sort_stay1.begin() + data_number / 2;std::vector sort_stay(first_, end_);std::sort(sort_stay.begin(), sort_stay.end(), sort_comp);//排序std::cout << "频率 | 幅值 | 相位" << std::endl;for (i = 0; i < show_number; i++) {std::cout << sort_stay[i].frequency << " | " << sort_stay[i].amplitude * 2.0 / double(data_number) << " | " << sort_stay[i].phase << std::endl;}}
}bool Fourier_transformer::no_prediction_power() {if (sorting.size() <= 2 || data_number_pre <= 0 || fit_parameter_have_solve == FALSE)return TRUE;elsereturn FALSE;
}bool Fourier_transformer::fit_funtion_pre_empty(trigonometric_function_paramater input_parameter) {if (input_parameter.A == 0 && input_parameter.B == 0 && input_parameter.C == 0)return TRUE;elsereturn FALSE;
}trigonometric_function_paramater Fourier_transformer::fit_trigonometric_function_paramater(double aomiga, int Fit_mode, double error_domain) {double sc = 0, c2 = 0, s2 = 0, s = 0, c = 0, y = 0, ys = 0, yc = 0, y2 = 0;//需要计算的取值int i = 0;double ti = 0, yi = 0;double value_ = 0, A = 0, B = 0, C = 0;double average = 0, derta = 0;//统计几何参数double number_ = 0;double judge_value = 0;Eigen::MatrixXd A_Matrix(3, 3), B_Matrix(3, 1), a_vector(3, 1);trigonometric_function_paramater output_;for (i = 0; i < Function_Points.size(); i++) {//循环赋值,从fuction points取数据ti = Function_Points[i].x * aomiga;yi = Function_Points[i].y;//std::cout <<"ti"<< Function_Points[i].y << std::endl;sc += sin(ti) * cos(ti);c2 += cos(ti) * cos(ti);s2 += sin(ti) * sin(ti);s += sin(ti);c += cos(ti);y += yi;ys += yi * sin(ti);yc += yi * cos(ti);y2 += yi * yi;}A_Matrix << c2, sc, c,sc, s2, s,c, s, double(data_number);B_Matrix << yc,ys,y;if (A_Matrix.determinant() != 0) {//安全//std::cout << A_Matrix.determinant() << std::endl;a_vector = (A_Matrix.inverse()) * B_Matrix;A = a_vector(0, 0); B = a_vector(1, 0); C = a_vector(2, 0);value_ = y2 + \A * A * c2 + \B * B * s2 + \2.0 * A * B * sc + \2.0 * A * C * c + \2.0 * B * C * s + \double(data_number) * C * C - \2.0 * A * yc - \2.0 * B * ys - \2.0 * C * y;output_.A = A; output_.B = B; output_.C = C; output_.omiga = aomiga; output_.error_value = value_;}else {output_.error_value = 99999999;}if (Fit_mode == FIT_DEDUCTING_ERROR_POINT) {//求统计学参数扣除坏点for (i = 0; i < Function_Points.size(); i++) {ti = Function_Points[i].x * aomiga;yi = Function_Points[i].y;average += yi - A * cos(ti) - B * sin(ti) - C;number_ = number_ + 1.0;}average /= number_;for (i = 0; i < Function_Points.size(); i++) {ti = Function_Points[i].x * aomiga;yi = Function_Points[i].y;derta += (yi - A * cos(ti) - B * sin(ti) - C - average) * (yi - A * cos(ti) - B * sin(ti) - C - average);}derta /= number_ - 1.0;derta = sqrt(derta);for (i = 0; i < Function_Points.size(); i++) {ti = Function_Points[i].x * aomiga;yi = Function_Points[i].y;judge_value = sqrt((yi - A * cos(ti) - B * sin(ti) - C) * (yi - A * cos(ti) - B * sin(ti) - C));if (judge_value > error_domain * derta) {Function_Points[i].is_error_point = TRUE;//std::cout << "error" << std::endl;}}number_ = 0;for (i = 0; i < Function_Points.size(); i++) {//循环赋值,从fuction points取数据if (Function_Points[i].is_error_point)continue;ti = Function_Points[i].x * aomiga;yi = Function_Points[i].y;sc += sin(ti) * cos(ti);c2 += cos(ti) * cos(ti);s2 += sin(ti) * sin(ti);s += sin(ti);c += cos(ti);y += yi;ys += yi * sin(ti);yc += yi * cos(ti);y2 += yi * yi;number_ = number_ + 1;}A_Matrix << c2, sc, c,sc, s2, s,c, s, number_;B_Matrix << yc,ys,y;if (A_Matrix.determinant() != 0) {//安全a_vector = (A_Matrix.inverse()) * B_Matrix;A = a_vector(0, 0); B = a_vector(1, 0); C = a_vector(2, 0);value_ = y2 + \A * A * c2 + \B * B * s2 + \2.0 * A * B * sc + \2.0 * A * C * c + \2.0 * B * C * s + \double(data_number) * C * C - \2.0 * A * yc - \2.0 * B * ys - \2.0 * C * y;output_.A = A; output_.B = B; output_.C = C; output_.omiga = aomiga; output_.error_value = value_;}else {output_.error_value = 99999999;}}return output_;
}double Fourier_transformer::DFT_random(double a, double b, double precision) {int OUTPUT = 0;double GAIN = 1;int i = 0;for (i = 0; i < precision; i++) {GAIN = GAIN * 10;}int A = a * GAIN, B = b * GAIN;OUTPUT = (rand() % (B - A + 1)) + A;double OUTPUT2 = 0;OUTPUT2 = OUTPUT;OUTPUT2 = OUTPUT2 / GAIN;return OUTPUT2;
}void Fourier_transformer::Solve_fit(int exquisite_number) {trigonometric_function_paramater this_function_parameters;//partical_swarm Q;double a = 0.5, b = 1;double now_position = DFT_random(a, b), new_position = DFT_random(a, b);double value_now = 0, value_new = 0;double d_value = 0;double best_aomiga = 0;int i = 0;int max_number = exquisite_number;int max_count = 0;double step = 0;a = 2.0 * Pi / double(data_number);b = 2.0 * Pi;step = abs(b - a) / max_number;value_now = fit_trigonometric_function_paramater(a).error_value;value_new = value_now;new_position = a;//partical_Function_Points = Function_Points;//start_c = clock();//Q.set_parameters(20, 1000);//Q.put_particals_in_region(a, b);//Q.calc_and_update(partical_fit_trigonometric_function_paramater);//best_aomiga = Q.get_best_parameter();//start_c = clock();max_count = ceil(0.5 * double(max_number));for (i = 0; i <= max_count; i++) {//利用梯度下降法value_new = fit_trigonometric_function_paramater(new_position).error_value;if (value_new < value_now) {value_now = value_new;best_aomiga = new_position;}new_position += step;}/*end_c = clock();std::cout <<"耗时:"<< end_c - start_c <<"毫秒" < 0) {cv::Mat show_mat(rows_, data_number * step_, CV_8UC3, cv::Scalar(255, 255, 255));cv::Point2d P1, P2, P3, P4;int i, i2;double max_data = *std::max_element(The_data_in_time.begin(), The_data_in_time.end());double min_data = *std::min_element(The_data_in_time.begin(), The_data_in_time.end());double A, B, C, w;double value_, value_1;max_data = DFT_max(abs(max_data), abs(min_data));A = fit_funtion_pre[0].A;B = fit_funtion_pre[0].B;C = fit_funtion_pre[0].C;w = fit_funtion_pre[0].omiga;for (i = 0; i < data_number; i++) {if (i < data_number - 1) {i2 = i + 1;value_ = A * cos(w * time_vector[i]) + B * sin(w * time_vector[i]) + C;value_1 = A * cos(w * time_vector[i2]) + B * sin(w * time_vector[i2]) + C;P1.x = double(i) * double(step_);P2.x = double(i2) * double(step_);P3.x = P1.x;P4.x = P2.x;P1.y = -The_data_in_time[i] * double(0.5 * double(rows_)) / (1.2 * max_data) + 0.5 * double(rows_);P2.y = -The_data_in_time[i2] * double(0.5 * double(rows_)) / (1.2 * max_data) + 0.5 * double(rows_);P3.y = -value_ * double(0.5 * double(rows_)) / (1.2 * max_data) + 0.5 * double(rows_);P4.y = -value_1 * double(0.5 * double(rows_)) / (1.2 * max_data) + 0.5 * double(rows_);}cv::line(show_mat, P3, P4, cv::Scalar(0, 0, 255), 4);cv::line(show_mat, P1, P2, cv::Scalar(255, 102, 5), 2);}cv::namedWindow("DFT input data", cv::WINDOW_NORMAL);cv::resizeWindow("DFT input data", cv::Size(1100, 400));cv::imshow("DFT input data", show_mat);cv::imwrite("E:\\Fit_pic.jpg", show_mat);cv::waitKey(5);}else {std::cout << "未输入数据!" << std::endl;}
}/****************************************************************************************************************/double one_partical::get_self_best_and_update_best() {std::vector STAY;STAY = self_history;std::sort(STAY.begin(), STAY.end(), one_partical_find_self_best);self_best_value = STAY[0].value;self_best_position = STAY[0].position;return STAY[0].position;
}void partical_swarm::set_patical_number(int input_partical_number) {patical_number = input_partical_number;
}partical_swarm::partical_swarm(int input_patical_number, int input_max_iteration) {Particals.resize(input_patical_number);patical_number = input_patical_number;max_iteration_number = input_max_iteration;srand(time(0));
}partical_swarm::partical_swarm() {srand(time(0));
}void partical_swarm::put_particals_in_region(double Lower, double Upper) {double step = 0;int i;if (patical_number <= 2) {patical_number = 10;}lower_ = Lower; upper_ = Upper;step = (Upper - Lower) / (double(patical_number) - 1.0);for (i = 0; i < patical_number; i++) {//等距放位置、速度Particals[i].position = double(i) * step;Particals[i].V = random_(Lower, 0.8 * Upper);Particals[i].self_best_position = double(i) * step;Particals[i].self_best_value = 99999999;Particals[i].now_value = 999999999;//std::cout << Particals[i].V << std::endl;}
}void partical_swarm::set_parameters(int input_partical_number, int input_max_iteration, double input_omiga_begin, double input_omiga_end, double input_self_index, double input_social_index) {omiga_begin = input_omiga_begin;omiga_end = input_omiga_end;self_index = input_self_index;social_index = input_social_index;max_iteration_number = input_max_iteration;patical_number = input_partical_number;Particals.resize(input_partical_number);
}void partical_swarm::calc_and_update(double (*value_function)(double)) {int i;/*更新位置和速度*/for (iteration_count = 0; iteration_count < max_iteration_number; iteration_count++) {//std::cout << iteration_count << std::endl;if (iteration_count <= 0) {global_best_position = Particals[1].position;global_best_value = value_function(global_best_position);}for (i = 0; i < patical_number; i++) {//更新位置和速度Particals[i].position += get_omiga(iteration_count) * Particals[i].V + \self_index * random_(0, 1) * (Particals[i].self_best_position - Particals[i].position) + \social_index * random_(0, 1) * (global_best_position - Particals[i].position);if(iteration_count > 7 * max_iteration_number / 10)Particals[i].position += 0.1 * random_(lower_,upper_);if (Particals[i].position > upper_ || Particals[i].position < lower_) {Particals[i].position = random_(lower_, upper_);}Particals[i].V = get_omiga(iteration_count) * Particals[i].V + \self_index * random_(0, 1) * (Particals[i].self_best_position - Particals[i].position) + \social_index * random_(0, 1) * (global_best_position - Particals[i].position);}for (i = 0; i < patical_number; i++) {//计算每个点的函数值,以及自身最优值更新Particals[i].now_value = value_function(Particals[i].position);Particals[i].historey_update(Particals[i].position, Particals[i].now_value);if (iteration_count <= 0) {Particals[i].self_best_position = Particals[i].position;Particals[i].self_best_value = Particals[i].now_value;}else {Particals[i].get_self_best_and_update_best();}}update_global_best();//更新全局最优值}
}void partical_swarm::update_global_best() {int i;sort_partical_self INpu;global_value_vector.clear();for (i = 0; i < patical_number; i++) {INpu.position = Particals[i].position;INpu.value = Particals[i].now_value;global_value_vector.push_back(INpu);}std::sort(global_value_vector.begin(), global_value_vector.end(), one_partical_find_self_best);global_best_position = global_value_vector[0].position;global_best_value = global_value_vector[0].value;/*std::cout << global_value_vector[0].value << std::endl;std::cout << global_value_vector[1].value << std::endl;*/if (global_best_value < best_value) {best_value = global_best_value;best_position = global_best_position;}
} 本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!