平衡二叉排序树(AVL)构造过程及Java代码实现

1、定义

平衡二叉排序树要求任何节点的左右子树高度差绝对值不超过1（左右子树高度可相同）。

2、普通二叉排序树不足

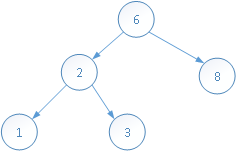
以依次插入1,2,3,4,5,6数为例，结果如下图所示：

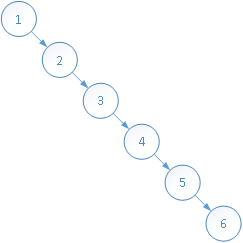
当查找元素6时，时间复杂度为O(n),并且这样构造相当于有一边的孩子节点失去了意义，这样就违背了二叉树的初衷。

3、平衡二叉排序树构造

       为了在不断向二叉排序树插入或者删除元素的过程中保持平衡性（即满足平衡二叉排序树定义要求），需要进行可能的四种操作：左单旋、右单旋、先右旋再左旋、先左旋再右旋。

（1）左单旋

插入：当前节点（值为1的节点）的右子树高度减去左子树高度大于1时，并且插入节点（值为3的节点）大于当前节点的右子节点值时需左单旋

删除：当前节点（值为1的节点）的右子树高度减去左子树高度大于1时，并且当前节点的右子节点的左子树高度小于右子树高度时需左单旋

（2）右单旋

插入：当前节点（值为3的节点）的左子树高度减去右子树高度大于1时，并且插入节点（值为1的节点）小于当前节点的左子节点值时需右单旋

删除：当前节点（值为3的节点）的左子树高度减去右子树高度大于1时，并且当前节点的左子节点的左子树高度大于右子树高度时需右单旋

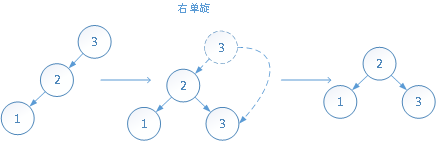
（3）先右旋再左旋

插入：当前节点（值为1的节点）的右子树高度减去左子树高度大于1时，并且插入节点（值为1.5的节点）小于当前节点的右子节点值时需先右旋再左旋

删除：当前节点（值为1的节点）的右子树高度减去左子树高度大于1时，并且当前节点的右子节点的左子树高度大于等于右子树高度时需先右旋再左旋

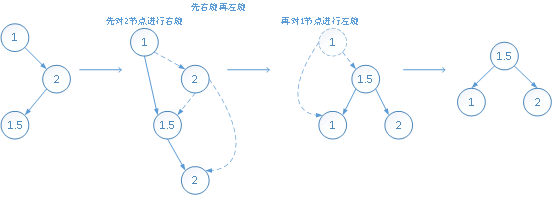
（4）先左旋再右旋

插入：当前节点（值为3的节点）的左子树高度减去右子树高度大于1时，并且插入节点（值为1的节点）大于当前节点的左子节点值时需先左旋再右旋

删除：当前节点（值为3的节点）的左子树高度减去右子树高度大于1时，并且当前节点的左子节点的左子树高度小于等于右子树高度时需先左旋再右旋

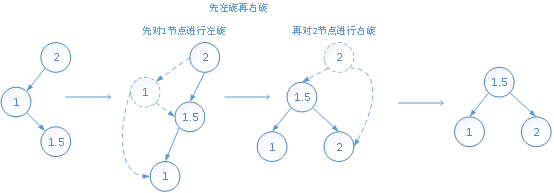
4、以给定的数组[3,2,1,4,5,6,7,10,9,8]进行平衡二叉排序树插入构造示例

插入元素3:

插入元素2:

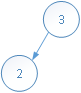
插入元素1:

插入元素4:

插入元素5:

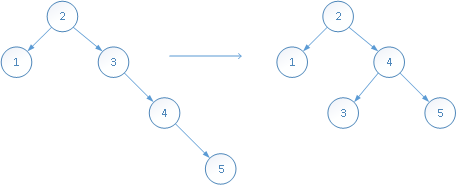
插入元素6:

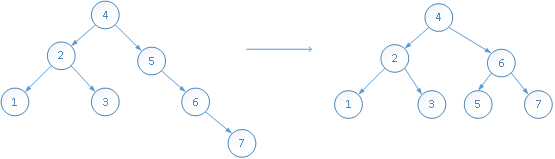
插入元素7:

插入元素10:

插入元素9:

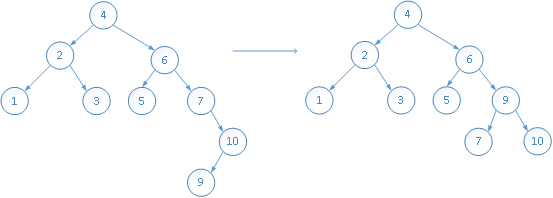
插入元素8:

5、已给定删除顺序7,9,10,5,4,6,3,2,8为例进行二叉排序树重新平衡示例

删除元素7：

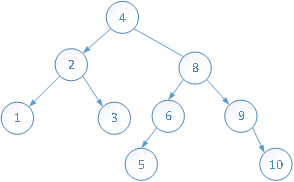
删除元素9：

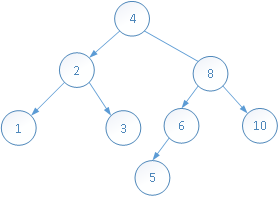
删除元素10：

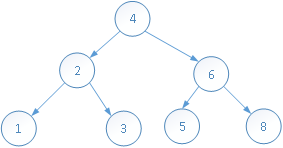
删除元素5：

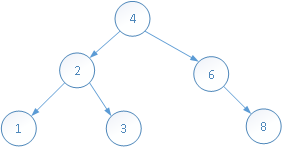
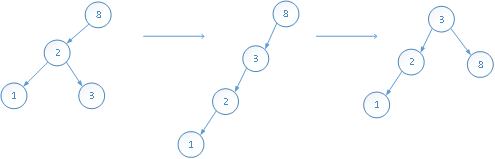
删除元素4：

删除元素6：

删除元素3：

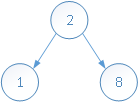
6、Java代码实现

package com.jingchenyong.boundless.algo;import java.util.Queue;
import java.util.concurrent.LinkedBlockingDeque;/*** 平衡二叉排序树代码实现* * @author henry**/
public class AvlTree {Queue queue = new LinkedBlockingDeque();// 按层遍历时所需队列private Tree root; // 二叉平衡排序树头节点public void insert(int data) {root = insert(root, data);}public void remove(int data) {root = remove(root, data);}/*** 插入操作* * @param root* @param data* @return*/public Tree insert(Tree root, int data) {if (root == null) {// 如果节点为null，那么就在此处插入那个新的节点，用来终止递归root = new Tree();root.data = data;return root;}if (data <= root.data) {root.leftChild = insert(root.leftChild, data); // 如果要插的值小于或等于当前的节点值，插入进左子树if (getHeight(root.leftChild) - getHeight(root.rightChild) > 1) {// 当前节点左子树高度减去右子树高度大于1时// 由于是向当前root树的左边插入，所以左子树高度必定不小于右子树高度if (data <= root.leftChild.data) {// 最后插入的叶子节点在该root树的左孩子的左边root = rightRotate(root); // 右旋，然后将调整后的root返回给其父节点的左子树域} else {// 最后插入的叶子节点在该root树的左孩子的右边root = leftAndRight(root); // 先左旋再右旋，然后将调整后的root返回给其父节点的左子树域}}} else {root.rightChild = insert(root.rightChild, data);// 如果要插的值大于当前的节点值，插入进右子树if (getHeight(root.rightChild) - getHeight(root.leftChild) > 1) {if (data <= root.rightChild.data) {root = rightAndLeft(root); // 先右旋再左旋，然后将调整后的root返回给其父节点的右子树域} else {root = leftRotate(root); // 左旋，然后将调整后的root返回给其父节点的右子树域}}}// 重新调整root节点的高度值（当插入新节点后，从这个节点到根节点的最短路径上的节点的高度值一定会发生改变，另外当出现失衡点时，这个失衡点的所有祖先节点的高度值也可能会发生改变）root.height = Math.max(getHeight(root.leftChild), getHeight(root.rightChild)) + 1;return root;}/*** 删除操作* * @param root* @param data* @return*/public Tree remove(Tree root, int data) {if (root == null) {// 没有找到删除的节点return null;}if (data < root.data) {// 在左子树上删除root.leftChild = remove(root.leftChild, data);if (getHeight(root.rightChild) - getHeight(root.leftChild) > 1) {if (getHeight(root.rightChild.leftChild) > getHeight(root.rightChild.rightChild)) {root = rightAndLeft(root);} else {root = leftRotate(root);}}} else if (data == root.data) {// 找到删除的节点if (root.leftChild != null && root.rightChild != null) {// 删除节点既有左子树也有右子树root.data = findNextNode(root).data; // 将右子树中最小值节点的值赋值给当前节点（表明当前节点已删除）root.rightChild = remove(root.rightChild, root.data);// 将问题转为删除当前节点的右子树中最小的节点// 如果是根节点删除也需要进行二叉平衡判断if (getHeight(root.leftChild) - getHeight(root.rightChild) > 1) {if (getHeight(root.leftChild.leftChild) > getHeight(root.leftChild.rightChild)) {root = rightRotate(root);} else {root = leftAndRight(root);}} else if (getHeight(root.rightChild) - getHeight(root.leftChild) > 1) {if (getHeight(root.rightChild.leftChild) > getHeight(root.rightChild.rightChild)) {root = rightAndLeft(root);} else {root = leftRotate(root);}}} else {// 删除节点只有左子树或者只有右子树或者为叶子节点的情况root = (root.leftChild == null) ? root.rightChild : root.leftChild;}} else {// 在右子树上删除root.rightChild = remove(root.rightChild, data);if (getHeight(root.leftChild) - getHeight(root.rightChild) > 1) {if (getHeight(root.leftChild.leftChild) > getHeight(root.leftChild.rightChild)) {root = rightRotate(root);} else {root = leftAndRight(root);}}}if (root != null) {root.height = Math.max(getHeight(root.leftChild), getHeight(root.rightChild)) + 1;}return root;}/*** 右单旋操作* * @param root* @return*/public Tree rightRotate(Tree root) {Tree temp = root.leftChild;root.leftChild = temp.rightChild;temp.rightChild = root;// 旋转后节点高度值再调整root.height = Math.max(getHeight(root.leftChild), getHeight(root.rightChild)) + 1;temp.height = Math.max(getHeight(root.leftChild), root.height) + 1;return temp;}/*** 左单旋操作* * @param root* @return*/public Tree leftRotate(Tree root) {Tree temp = root.rightChild;root.rightChild = temp.leftChild;temp.leftChild = root;// 旋转后节点高度值再调整root.height = Math.max(getHeight(root.leftChild), getHeight(root.leftChild)) + 1;temp.height = Math.max(getHeight(temp.leftChild), getHeight(temp.leftChild)) + 1;return temp;}/*** 先左旋再右旋操作* * @param root* @return*/public Tree leftAndRight(Tree root) {root.leftChild = leftRotate(root.leftChild);return rightRotate(root);}/*** 先右旋再左旋操作* * @param root* @return*/public Tree rightAndLeft(Tree root) {root.rightChild = rightRotate(root.rightChild);return leftRotate(root);}/*** 找到右子树下最小节点* * @param root* @return*/public Tree findNextNode(Tree root) {if (root == null) {return null;}Tree r = root.rightChild;while (r != null && r.leftChild != null) {r = r.leftChild;}return r;}/*** 获取当前节点的高度* * @param node* @return*/public int getHeight(Tree node) {return node == null ? -1 : node.height;}/*** 获取树节点的高度(方法二)* * @param node* @return*//*public int getHeight(Tree node) {if (node == null) {return -1;}if (node.leftChild == null && node.rightChild == null) {return 0;} else if (node.leftChild == null && node.rightChild != null) {return getHeight(node.rightChild) + 1;} else if (node.leftChild != null && node.rightChild == null) {return getHeight(node.leftChild) + 1;} else {if (getHeight(node.leftChild) < getHeight(node.rightChild)) {return getHeight(node.rightChild) + 1;} else {return getHeight(node.leftChild) + 1;}}}*//*** 中序遍历* * @param node*/public void middle(Tree node) {if (node == null) {return;}middle(node.leftChild);System.out.println(node.data);middle(node.rightChild);}/*** 按层遍历* * @param queue*/public void floorShow(Queue queue) {Tree currentNode;while ((currentNode = queue.poll()) != null) {System.out.println(currentNode.data);if (currentNode.leftChild != null) {queue.offer(currentNode.leftChild);}if (currentNode.rightChild != null) {queue.offer(currentNode.rightChild);}floorShow(queue);}}/*** 平衡二叉排序树节点* * @author Administrator**/private static class Tree {public Tree leftChild;public Tree rightChild;public int data;// 记录节点的数据public int height;// 记录节点的高度}public static void main(String[] args) {AvlTree avlTree = new AvlTree();avlTree.insert(3);avlTree.insert(2);avlTree.insert(1);avlTree.insert(4);avlTree.insert(5);avlTree.insert(6);avlTree.insert(7);avlTree.insert(10);avlTree.insert(9);avlTree.insert(8);System.out.println("中序遍历:");avlTree.middle(avlTree.root);System.out.println("按层遍历:");avlTree.queue.offer(avlTree.root);avlTree.floorShow(avlTree.queue);System.out.println();avlTree.remove(7);avlTree.remove(9);avlTree.remove(10);avlTree.remove(5);avlTree.remove(4);avlTree.remove(6);System.out.println("中序遍历:");avlTree.middle(avlTree.root);System.out.println("按层遍历:");avlTree.queue.offer(avlTree.root);avlTree.floorShow(avlTree.queue);}
}

代码运行结果：

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！