2024王道数据结构大题p143-p144（一）

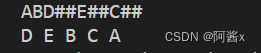
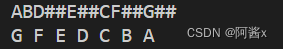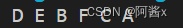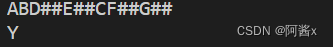二叉树

• • 1.编写后序遍历二叉树的非递归算法
  • 2.试给出二叉树的自下而上，从右到左的层次遍历算法。
  • 3.假设二叉树采用二叉链表存储结构，设计非递归算法求二叉树的高度。
  • 4.设一颗二叉树中各结点的值互不相同，其先序遍历序列和中序遍历序列分别存在与两个一维数组A[1...n]和B[1...n]中，试编写算法建立该二叉树的二叉链表。
  • 5.二叉树按照二叉链表形式存储，试编写一个判别给定二叉树是否是完全二叉树的算法。
  • 6.假设二叉树采用二叉链表存储结构存储，试设计一个算法，计算给定二叉树的所有双分支结点的个数。
  • 7.设树B是一颗采用链式结构存储的二叉树，编写一个把树B中所有结点的左、右子树进行交换的函数。
  • 8.假设二叉树采用二叉链表存储结构存储，设计一个算法，求先序遍历中第k（1<=k<=二叉树中结点的个数）个结点的值
  • 9.以知一颗二叉树以二叉链存储结构存储，编写算法完成：对于树中每个元素值为x的结点，删除已它为根的子树，并释放相应的空间；

1.编写后序遍历二叉树的非递归算法

• 算法的基本设计思想
  采用一个辅助栈实现非递归算法，先沿着左分支遍历并依次压栈，没有右孩子就弹出栈并输出，然后沿着右分支压栈。
• 算法实现

// 编写后序遍历二叉树的非递归算法
#include 
using namespace std;
typedef struct TreeNode
{char data;TreeNode *lchild, *rchild;int tag;
} TreeNode, *Tree; // Tree= TreeNode *;
void creattree(Tree &t)
{char ch;ch = getchar();if (ch == '#')t = NULL;else{t = (Tree)malloc(sizeof(TreeNode));t->data = ch;t->lchild = NULL;t->rchild = NULL;t->tag = 0;creattree(t->lchild);creattree(t->rchild);}
}
void back(Tree t)
{struct TreeNode *stack[100];int top = -1;TreeNode *p = t;while (p || top != -1)//栈空结点空就遍历完退出循环{if (p)//沿着左分支压栈{stack[++top] = p;p = p->lchild;}else{p = stack[top];//弹出栈顶元素/第一次弹出的是最左边的元素if (p->rchild && p->rchild->tag == 0)//弹出的元素有右孩子并且未访问过p = p->rchild;//p移到右孩子else{p = stack[top];top--;          //否则退栈cout << p->data << " ";//输出栈顶元素p->tag = 1;//然后将p的访问位置为1p = NULL; // 重置p不然又压入栈中}}}
}
int main()
{Tree t;creattree(t);back(t);return 0;
}
//ABDEC
//ABD##E##C##

• 小结
  实现过程中要注意重置p工作指针并需要使用一个tag访问位。

2.试给出二叉树的自下而上，从右到左的层次遍历算法。

• 算法的基本设计思想
  层次遍历很容易想到使用队列实现，然后需要自下而上，从右到左就是一个逆序的层次所以想到使用栈。
• 算法实现

//试给出二叉树的自下而上，从右到左的层次遍历算法。
#include 
using namespace std;
#define Max 10
typedef struct TreeNode
{char data;TreeNode *rchild, *lchild;} TreeNode, *Tree;
void creattree(Tree &t)
{char ch;ch = getchar();if (ch == '#')t = NULL;else{t = (Tree)malloc(sizeof(TreeNode));t->data = ch;t->rchild = NULL;t->lchild = NULL;creattree(t->lchild);creattree(t->rchild);}
}
typedef struct stack1
{struct TreeNode *data[Max]; // 栈中存的是树的结点int top;
} stack1;
bool isempty(stack1 s)
{if (s.top == -1)return true;returnfalse;
};
bool isfull(stack1 s)
{if (s.top == Max - 1)return true;returnfalse;
}
bool push(stack1 &s, TreeNode *p)
{if (isfull(s))return false;s.data[++s.top] = p;return true;};
bool pop(stack1 &s, TreeNode *&p)
{if (isempty(s)){return false;}p = s.data[s.top--];return true;}
struct squeue1
{struct TreeNode *data[Max];int f, r, tag;
};
bool EnQueue(squeue1 &q, TreeNode *p)
{if (q.r == q.f && q.tag == 1){cout << "队满" << endl;return false;}q.data[q.r] = p;q.r=(q.r+1)%Max;q.tag = 1;return true;}
bool DeQueue(squeue1 &Q, TreeNode *&p)
{if (Q.r == Q.f && Q.tag == 0){cout << "队空" << endl;return false;}p = Q.data[Q.f];Q.f=(Q.f+1)%Max;Q.tag = 0;return true;}void InvertLevel(Tree t)
{squeue1 q;stack1 s;TreeNode *p ;if(t){s.top=-1;q.f=q.r=q.tag=0;EnQueue(q,t);while (!(q.f==q.r&&q.tag==0)){DeQueue(q,p);push(s,p);if(p->lchild) EnQueue(q,p->lchild);if(p->rchild)EnQueue(q,p->rchild);}  while (!isempty(s)){pop(s,p);cout<<p->data<<" ";}}
}int main()
{Tree T;creattree(T);InvertLevel(T);return 0;
};
/*A                    B    C                  D  E  F  G                   
ABD##E##CF##G##                   
*/

• 小结

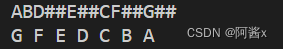
3.假设二叉树采用二叉链表存储结构，设计非递归算法求二叉树的高度。

• 算法的基本设计思想
  求高度，想到层次遍历，用L指向一层最后一个元素
• 算法实现

// 假设二叉树采用二叉链表存储结构，设计非递归算法求二叉树的高度。
#include 
using namespace std;
#define Max 10
typedef struct TreeNode
{char data;TreeNode *rchild, *lchild;} TreeNode, *Tree;
void creattree(Tree &t)
{char ch;ch = getchar();if (ch == '#')t = NULL;else{t = (Tree)malloc(sizeof(TreeNode));t->data = ch;t->lchild = NULL;t->rchild = NULL;creattree(t->lchild);creattree(t->rchild);}
}
int getH(Tree t)
{if (!t)return 0;TreeNode *queue[Max];int dep = 0;int r = -1, f = -1;int L = 0; // 下一层最后一个结点的下标，TreeNode *p;queue[++r] = t;while (f < r) // 层次遍历的循环条件队尾大于对头{p = queue[++f];if (p->lchild)queue[++r] = p->lchild;if (p->rchild)queue[++r] = p->rchild;if (L == f){          // 如果L等于一层中最后一个结点的下标dep++; // 高度加一L = r; // L指向下一层中最后一个结点的下标；}}return dep;
}
int main()
{Tree t;creattree(t);cout << getH(t);return 0;
}

• 小结
  重点是分析出层次直接的关系，利用好一层最后一个结点

4.设一颗二叉树中各结点的值互不相同，其先序遍历序列和中序遍历序列分别存在与两个一维数组A[1…n]和B[1…n]中，试编写算法建立该二叉树的二叉链表。

• 算法的基本设计思想
  B的中序遍历左根右边将每次可将树划分为左右子树，A依次遍历每个结点都是B中某树的根结点利用这个关系去做一个递归建立二叉树。
• 算法实现

//设一颗二叉树中各结点的值互不相同，其先序遍历序列和中序遍历序列分别存在与两个一维数组A[1...n]和B[1...n]中，试编写算法建立该二叉树的二叉链表。
#include 
using namespace std;
char a[] = {'A', 'B', 'D', 'E', 'C', 'F'};
char b[] = {'D', 'B', 'E', 'A', 'F', 'C'};
typedef struct TreeNode
{char data;TreeNode *lchild, *rchild;
} TreeNode, *Tree;
int pos = 0; // 根节点下标
Tree creattree(char a[], char b[], int s, int e)//s，e是b[]的左右下标
{ // start endif (s <= e)//递归退出条件左边大于右边就退出也就是叶子结点的地方{TreeNode *root = (TreeNode *)malloc(sizeof(TreeNode));root->data = a[pos++];//遍历下一个树的根节点int i;for (i = s; i <= e; i++)if (root->data == b[i])//分为左右树break;root->lchild = creattree(a, b, s, i - 1);root->rchild = creattree(a, b, i + 1, e);return root;//}return NULL;
}
void disp(Tree t)
{if (t){disp(t->lchild);disp(t->rchild);cout << t->data << " ";}
}
int main()
{Tree root = creattree(a, b, 0, 5);disp(root);return 0;
}
//         A
//       /    \
//      B       C
//    /  \     /
//   D    E   F

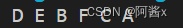
• 小结
  抓住好先序和中序的一个关系， 中序可以划分左右子树，先序的第一个结点都是根结点；

5.二叉树按照二叉链表形式存储，试编写一个判别给定二叉树是否是完全二叉树的算法。

• 算法的基本设计思想
  采用层次遍历。是否是完全二叉树的判定
  1）结点无左孩子，必无右孩子
  2）结点缺孩子（缺左孩子或缺右孩子），遍历接下来的结点必无孩子
  用个flag来判断是否缺孩子
• 算法实现

// 二叉树按照二叉链表形式存储，试编写一个判别给定二叉树是否是完全二叉树的算法。
#include 
using namespace std;
#define Max 15
typedef struct treenode
{char data;treenode *rchild, *lchild;
} treenode, *tree;
void buildtree(tree &t)
{char ch;ch = getchar();if (ch == '#')t = NULL;else{t = (tree)malloc(sizeof(treenode));t->data = ch;t->lchild = NULL;t->rchild = NULL;buildtree(t->lchild);buildtree(t->rchild);}
}
struct squeue
{struct treenode *data[Max];int r, f, tag;
};
bool isempty(squeue s)
{if (s.f == s.r && s.tag == 0)return true;return false;
}
bool isfull(squeue s)
{if (s.f == s.r && s.tag == 1)return true;return false;
}
bool enters(squeue &s, treenode *p)
{if (isfull(s))return false;s.data[(s.r++) % Max] = p;s.tag = 1;return true;
}
bool outs(squeue &s, treenode *&p)
{if (isempty(s))return false;p = s.data[(s.f++) % Max];s.tag = 0;return true;
}
bool isok(tree t)
{squeue s;s.f = s.r = s.tag = 0;bool flag = true, ans = true; // flag表示孩子是否缺少，ans表示结果是否为完全二叉树if (t == NULL)ans = true;               // 空树是完全二叉树；if (!t->lchild && !t->rchild) // 根节点无左右还是孩子也是满足ans = true;enters(s, t);treenode *p;        // 工作指针pwhile (!isempty(s)) // 层次遍历{outs(s, p);if (!p->lchild) /// 没有左孩子{flag = false;if (p->rchild) // 有右孩子 ans=falseans = false;}else // 有左孩子{if (flag) // 之前不存在缺孩子的结点{enters(s, p->lchild); // 有左孩子左孩子进队if (p->rchild)enters(s, p->rchild); // 有右孩子右孩子进队elseflag = false; // flag==false}else // 之前存在缺孩子的结点，然后这个结点又有左孩子 ans=falseans = false;}}if (ans)return true;return false;
}
int main()
{tree t;buildtree(t);if (isok(t))cout << "Y" << endl;elsecout << "N" << endl;return 0;
}
// ABD##E##CF##G## 完全
// ABD###CE##F##  非完全

• 小结
  层次遍历，抓住完全二叉树的判定。

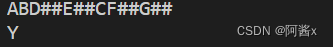
6.假设二叉树采用二叉链表存储结构存储，试设计一个算法，计算给定二叉树的所有双分支结点的个数。

• 算法的基本设计思想
  采用递归，判断结点是否有左右孩子，如果有左右孩子（即双分支结点）然后分别向左右孩子递归并+1；递归退出条件是结点空，函数返回类型是int，return找到+1；
• 算法实现

//假设二叉树采用二叉链表存储结构存储，试设计一个算法，计算给定二叉树的所有双分支结点的个数
#include 
using namespace std;
typedef struct treenode {char data ;treenode *rchild,*lchild;
}treenode ,*tree;void buildtree(tree &t){char ch;ch=getchar();if(ch=='#') t=NULL;else{t=(tree)malloc(sizeof(treenode ));t->data=ch;t->lchild=NULL;t->rchild=NULL;buildtree(t->lchild);buildtree(t->rchild);}}void disp(tree &t){if (t){cout<<t->data<<" ";disp(t->lchild);disp(t->rchild);}}int   countdouble(tree &t){if(!t) return 0;else if(t->lchild&&t->rchild)//找到双分支结点，然后分别向左右孩子递归return countdouble(t->lchild)+countdouble(t->rchild)+1;else return countdouble(t->lchild)+countdouble(t->rchild);}
int main(){tree t;buildtree(t);disp(t);int result =countdouble(t);cout<<result<<endl;return 0;
}
/*A/  \B    C/\     /  \D E    F   G*/
//前序序列:ABD##E##CF##G##

• 小结
  这种int函数返回类型，return f()+1，需要掌握好。

7.设树B是一颗采用链式结构存储的二叉树，编写一个把树B中所有结点的左、右子树进行交换的函数。

• 算法的基本设计思想
  显然也是一道用递归很好实现的题，先沿左下递归，然后右下递归然后交换左右
• 算法实现

//设树B是一颗采用链式结构存储的二叉树，编写一个把树B中所有结点的左、右子树进行交换的函数。
#include 
using namespace std;
typedef struct treenode {char data ;treenode *lchild, *rchild;
}treenode ,*tree;
void buildtree(tree &t)
{char ch;ch=getchar();if(ch=='#') t=NULL;else{t=(tree)malloc(sizeof(treenode));t->data=ch;t->lchild=NULL;t->rchild=NULL;buildtree(t->lchild);buildtree(t->rchild);}
}
void disp(tree &t){if(t){cout<<t->data<<" ";disp(t->lchild);disp(t->rchild);}}
void swaplr(tree &t)
{treenode *p;if(t){swaplr(t->lchild);swaplr(t->rchild);p=t->lchild;t->lchild=t->rchild;t->rchild=p;}
}
int main(){tree t;buildtree(t);disp(t);cout<<endl;swaplr(t);disp(t);return 0;
}
/*A/  \B    C/\     /  \D E    F   G*/
//前序序列:ABD##E##CF##G##

• 小结
  FF DO类型，函数（）+函数（）+操作；

8.假设二叉树采用二叉链表存储结构存储，设计一个算法，求先序遍历中第k（1<=k<=二叉树中结点的个数）个结点的值

• 算法的基本设计思想
  用递归先序遍历实现，先赋值给全局int i=1，先（i==k）判断是不是要找的，不是就i++然后找先序遍历的下一个，没找到ch=‘#’，找到ch=data，然后返回ch；
• 算法实现

// 假设二叉树采用二叉链表存储结构存储，设计一个算法，求先序遍历中第k（1<=k<=二叉树中结点的个数）个结点的值
#include 
using namespace std;
typedef struct treenode
{char data;treenode *lchild, *rchild;
} treenode, *tree;
void buildtree(tree &t)
{char ch;ch = getchar();if (ch == '#')t = NULL;else{t = (tree)malloc(sizeof(treenode));t->data = ch;t->lchild = NULL;t->rchild = NULL;buildtree(t->lchild);buildtree(t->rchild);}
}
int i = 1;
char ch;
char fink(tree &t, int &k) // 1<=k<=二叉树中结点的个数
{if (!t)return '#'; // 有两个退出递归情况因此在下面要对这两个情况做出判断if (i == k)return t->data;i++;ch = fink(t->lchild, k);if (ch != '#') // ch==#就是左边没找到然后去右边找，!=#就是找到了，然后一路返回最后退出递归return  ch;return ch;ch = fink(t->rchild, k);return ch; // 这里找到就是返回result没找到就是返回（'#'）。
}
int main()
{tree t;buildtree(t);int k = 5;cout << fink(t, k);return 0;
} // ABD##E##CF##G##;

• 小结
  就是给先序遍历的结点赋值1,2,3…n

9.以知一颗二叉树以二叉链存储结构存储，编写算法完成：对于树中每个元素值为x的结点，删除已它为根的子树，并释放相应的空间；

• 算法的基本设计思想
  先做一个ffdo的后序递归删除树的函数，然后再写删除x为结点函数，也是用递归实现，找到就删除然后注意删除后要置为空。王道书上的代码freex2没跑出来。
• 算法实现

// 以知一颗二叉树以二叉链存储结构存储，编写算法完成：对于树中每个元素值为x的结点，删除已它为根的子树，并释放相应的空间；
#include //freex1可用，freex2（王道书上的代码）没跑出来！！！
using namespace std;
#define Max 10
typedef struct treenode
{char data;treenode *lchild, *rchild;} treenode, *tree;
void buildtree(tree &t)
{char ch;ch = getchar();if (ch == '#')t = NULL;else{t = (tree)malloc(sizeof(treenode));t->data = ch;t->rchild = NULL;t->lchild = NULL;buildtree(t->lchild);buildtree(t->rchild);}
}void disp(tree &t)
{if (t){cout << t->data << " ";disp(t->lchild);disp(t->rchild);}
}
void detree(tree &t)
{if (t){detree(t->lchild);detree(t->rchild);free(t);}
}
void freex1(tree &t, char &x)
{if (!t)return;if (t->data == x){detree(t);t = NULL;//注意删除后要将t置为NULL}else{freex1(t->lchild, x);freex1(t->rchild, x);}
}
typedef struct queue
{treenode *data[Max];int r, f, tag;
} queue;
bool enquque(queue &s, treenode *x)
{if (s.f == s.r && s.tag == 1)return false;s.data[(s.r++) % Max] = x;s.tag = 1;return true;
}
bool dequeue(queue &s, treenode *&x)
{if (s.f == s.r && s.tag == 0)return false;x = s.data[(s.f++) % Max];s.tag = 0;return true;
}
void freex2(tree &t, char x)
{queue s;treenode *p;s.f = s.r = s.tag = 0;if (t){                 // 树不为空再判断t->data == x; // 如果树为空。t->data为报错(null->data,这不存在)；detree(t);}enquque(s, t);while (!(s.f == s.r && s.tag == 0)){dequeue(s, p);if (p->lchild){ // 先判断p的左孩子是否存在if (p->lchild->data == x){                      // p的左孩子满足删掉p的左孩子detree(p->lchild); //p->lchild = NULL;  // 注意！p的左孩子要指向空；}elseenquque(s, p->lchild); // 没找到则入队}if (p->rchild) // 再判断p的右孩子是否存在{if (p->rchild->data == x){detree(p->rchild);p->rchild = NULL;}elseenquque(s, p->rchild);}}
}
int main()
{tree t;buildtree(t);disp(t);char ch = 'C';freex1(t, ch);disp(t);return 0;
}
/*ABD##E##CF##G##*/

• 小结
  递归递归递归递归递归递归递归递归递归递归递归递归！！！！~~~

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！