统计建模笔记7 残差分析

残差

• 定义残差是响应变量中回归模型所未解释的变异 性度量：
  e i = y i − y ^ + i e_i = y_i − \hat y+i ei​=yi​−y^​+i
  其中 y i y_i yi​ 表示样本的观测值， y ^ i \hat y_i y^​i​ 表示样本的预测值

  • 残差是模型误差的观测值, 误差的任何对基本假设的违背都可以通过残差体现出来
  • 残差分析是探索几种模型不适用性类型的有效办法

• 用向量来描述 $n$ 个数据的残差，记为： e = y − y ^ e = y − \hat y e=y−y^​ 其中 y ^ = X β ^ \hat y = X \hat β y^​=Xβ^​.

• 将最小二乘估计的结果 β ^ = ( X T X ) − 1 X T y \hat β = (X^TX) ^{−1}X^Ty β^​=(XTX)−1XTy 代入其 中，有回归向量：
  y ^ = X ( X T X ) − 1 X T y = H y \hat y = X(X^TX)^{−1}X^T y = Hy y^​=X(XTX)−1XTy=Hy
  其中 H = X ( X T X ) − 1 X T H = X(X^TX)^{−1}X^T H=X(XTX)−1XT 称为帽子矩阵。可以证明，帽子矩阵是幂等对称矩阵，具有如下的性质：

  • H T = H H^T = H HT=H
  • H 2 = H H^2 = H H2=H
  • $(I-H)X=0$
  • $(I-H)H=0$

• 残差向量可以表示为：
  e = y − y ^ = ( I − H ) y = ( I − H ) ( X β + e ) = ( I − H ) e e = y−\hat y = (I−H)y = (I−H)(Xβ + e) = (I−H)e e=y−y^​=(I−H)y=(I−H)(Xβ+e)=(I−H)e
  残差向量实际上是对误差项的一个估计量。关于 残差，有如下的性质：

定理

对残差向量，我们有：

(1) E ( e ^ ) = 0 , c o v ( e ^ ) = σ 2 ( I − H ) E(\hat e) = 0, cov(\hat e) = σ^2 (I−H) E(e^)=0,cov(e^)=σ2(I−H)

(2) 若进一步假设误差向量 e ∼ N ( 0 , σ 2 I ) e \sim N(0, σ^2 I) e∼N(0,σ2I)，则 e ^ ∼ N ( 0 , σ 2 ( I − H ) ) \hat e \sim N(0, σ^2 (I − H)) e^∼N(0,σ2(I−H))

(3) e ^ \hat e e^ 和 y ^ \hat y y^​ 相互独立， c o v ( e ^ , y ^ ) = 0 cov(\hat e, \hat y) = 0 cov(e^,y^​)=0

方差齐性检验

注意到：
v a r ( e ^ i ) = σ 2 ( 1 − h i i ) var(\hat e_i) = σ^2(1 − h_{ii}) var(e^i​)=σ2(1−hii​)
可见在一般情况下，ˆei 的方差是不相等的。因此 我们不能直接使用残差来检验方差齐性，需要首 先对残差尺度化，记：
r i = e ^ i v a r ( e ^ i ) = e ^ i σ 2 1 − h i i ri = \frac{\hat e_i}{\sqrt {var(\hat e_i)}} = \frac{\hat e_i}{\sigma^2 \sqrt {1-h_{ii}}} ri=var(e^i​) ​e^i​​=σ21−hii​ ​e^i​​
其中 σ ^ 2 = S S E ( n − p ) \large \hat σ^2 = \Large \frac{SSE}{(n − p)} σ^2=(n−p)SSE​.

r i r_i ri​ 近似服从正态分布 r i ∼ N ( 0 , 1 ) r_i \sim N(0, 1) ri​∼N(0,1)

因而，
P ( − 2 ≤ r i ≤ 2 ) = 95.5 % , i = 1 , 2 , ⋅ ⋅ ⋅ , n P(−2 ≤ r_i ≤ 2) = 95.5\%, ~~~i = 1, 2, · · · , n P(−2≤ri​≤2)=95.5%,   i=1,2,⋅⋅⋅,n
即一个观测样本的残差有 95.5% 的概率落在区间 [−2, 2] 之间。

如果违背了这一点，我们就有理由拒绝方差齐性假设。

残差图分析

分析：

（a）对所有 $x$ 值，$e$ 的方差都相同，且描述变量 $x$ 和 $y$ 之间的回归模型是合理的，残差图中的所有点落在一条水平带中间。

（b）对所有的值，$e$ 的方差是不同的，对于较大的 $x$ 值，相应的残差也较大，违背了 $e$ 的方差相等的假设

（c）表明所选的回归模型不合理，应考虑曲线回归或多元回归模型。

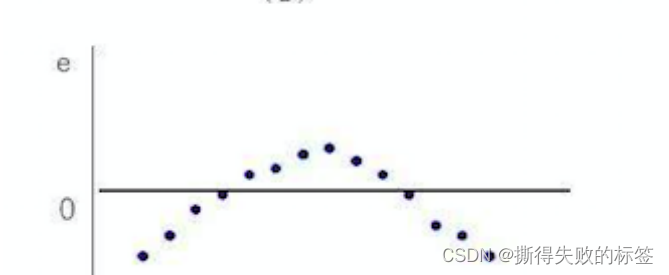
表明 $y$ 与 $X$ 之间不是线性关系，应该考虑 使用曲线回归来拟合样本观测值；

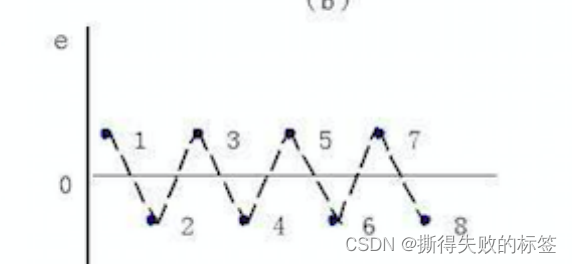
蛛网现象，表明 $Y$ 存在自相关

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！