特征工程典型方法

一、主成分分析法

背景

在许多领域的研究与应用中，通常需要对含有多个变量的数据进行观测，收集大量数据后进行分析寻找规律。多变量大数据集无疑会为研究和应用提供丰富的信息，但是也在一定程度上增加了数据采集的工作量。更重要的是在很多情形下，许多变量之间可能存在相关性，从而增加了问题分析的复杂性。如果分别对每个指标进行分析，分析往往是孤立的，不能完全利用数据中的信息，因此盲目减少指标会损失很多有用的信息，从而产生错误的结论。
因此需要找到一种合理的方法，在减少需要分析的指标同时，尽量减少原指标包含信息的损失，以达到对所收集数据进行全面分析的目的。由于各变量之间存在一定的相关关系，因此可以考虑将关系紧密的变量变成尽可能少的新变量，使这些新变量是两两不相关的，那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。主成分分析与因子分析就属于这类降维算法。

数据降维

降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的。在实际的生产和应用中，降维在一定的信息损失范围内，可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法。
降维具有如下一些优点：

1. 使得数据集更易使用。
2. 降低算法的计算开销。
3. 去除噪声。
4. 使得结果容易理解。

降维的算法有很多，比如奇异值分解(SVD)、主成分分析(PCA)、因子分析(FA)、独立成分分析(ICA)。

PCA的概念

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。
PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

由于得到协方差矩阵的特征值特征向量有两种方法：特征值分解协方差矩阵、奇异值分解协方差矩阵，所以PCA算法有两种实现方法：基于特征值分解协方差矩阵实现PCA算法、基于SVD分解协方差矩阵实现PCA算法。

协方差和散度矩阵

样本的均值：

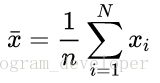
样本的方差：

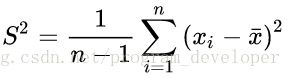
X与Y的协方差：

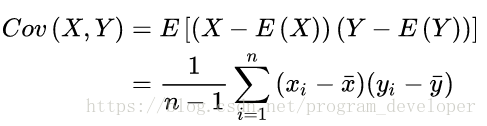
有以上公式，我们得出：
(1) 方差的计算公式是针对一维特征，即针对同一特征不同样本的取值来进行计算得到；而协方差则必须要求至少满足二维特征；方差是协方差的特殊情况。
(2) 方差和协方差的除数是n-1,这是为了得到方差和协方差的无偏估计。
协方差为正时，说明X和Y是正相关关系；协方差为负时，说明X和Y是负相关关系；协方差为0时，说明X和Y是相互独立。

PCA实例

（1）PCA的python实现

##Python实现PCA
import numpy as np
def pca(X,k):#k is the components you want#mean of each featuren_samples, n_features = X.shapemean=np.array([np.mean(X[:,i]) for i in range(n_features)])#normalizationnorm_X=X-mean#scatter matrixscatter_matrix=np.dot(np.transpose(norm_X),norm_X)#Calculate the eigenvectors and eigenvalueseig_val, eig_vec = np.linalg.eig(scatter_matrix)eig_pairs = [(np.abs(eig_val[i]), eig_vec[:,i]) for i in range(n_features)]# sort eig_vec based on eig_val from highest to lowesteig_pairs.sort(reverse=True)# select the top k eig_vecfeature=np.array([ele[1] for ele in eig_pairs[:k]])#get new datadata=np.dot(norm_X,np.transpose(feature))return dataX = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
print(pca(X,1))

(2)sklearn的PCA：

from sklearn.decomposition import PCA
import numpy as np
X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca=PCA(n_components=1).fit(X)
print(pca.transform(X))

先创建一个PCA对象，其中参数n_components表示保留的特征数，默认为1。如果设置成‘mle’,那么会自动确定保留的特征数

两者所得到的效果完全一致

5. PCA的理论推导

通俗易懂的解释：（1）最大方差理论（2）最小化降维后的损失

最大方差理论

在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。样本在u1上的投影方差较大，在u2上的投影方差较小，那么可认为u2上的投影是由噪声引起的。

因此我们认为，最好的k维特征是将n维样本点转换为k维后，每一维上的样本方差都很大。

如何选取最好的值

两个概念：

选择不同的K值，然后用下面的式子不断计算，选取能够满足下列式子条件的最小K值即可。

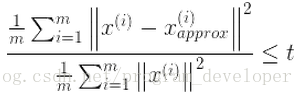
其中的t值可以表示精度，t如果为0.02，则表示保留了目标98%的信息。

二、熵权法

方法介绍

越有可能发生的事情，信息量越少。越不可能发生的事情，信息量就越多。其中我们认为 概率 就是衡量事情发生的可能性大小的指标。
将信息量用I表示，p表示概率，可得到以下函数：

那么，假设 x 表示事件 X 可能发生的某种情况，p(x)表示这种情况发生的概率情况如上图所示，该图像可以用对数函数进行拟合，那么最终我们可以定义：I ( x ) = − ln ⁡ ( p ( x ) ) I(x) = -\ln(p(x))I(x)=−ln(p(x))，因为 0 ≤ p ( x ) ≤ 1 0 ≤ p(x) ≤ 10≤p(x)≤1，所以 I ( x ) ≥ 0 I(x) ≥ 0I(x)≥0。

信息熵的定义

假设 x 表示事件 X 可能发生的某种情况，p(x) 表示这种情况发生的概率我们可以定义:I( x ) = − ln ⁡ ( p ( x ) ) ，因为0 ≤ p ( x ) ≤ 1 ，0≤p(x)≤10≤p(x)≤1 ，所以I(x)≥0 。 如果事件 X 可能发生的情况分别为: x 1 , x 2 , ⋯   , x n 那么我们可以定义事件 X XX 的信息熵为：

可以证明的是： p ( x 1 ) = p ( x 1 ) = ⋯ = p ( x n ) = 1 / n 时，H(x) 取最大值，此时 H ( x ) = ln ⁡ ( n ) H(x)=\ln(n)H(x)=ln(n)。 (n表示事件发生情况的总数)

熵权法的计算步骤

熵权法的计算步骤大致分为以下三步：

1. 判断输入的矩阵中是否存在负数，如果有则要重新标准化到非负区间（后面计算概率时需要保证每一个元素为非负数）。
2. 计算第 j 项指标下第 i 个样本所占的比重，并将其看作相对熵计算中用到的概率。
3. 计算每个指标的信息熵，并计算信息效用值，并归一化得到每个指标的熵权。

代码实现

import pandas as pd
import numpy as np
import math
from numpy import array# 定义熵值法函数  熵值法计算变量的权重
def cal_weight(df):#求krows = df.index.size  # 行cols = df.columns.size  # 列k = 1.0 / math.log(rows)# 矩阵计算、信息熵x = array(df)lnf = [[None] * cols for i in range(rows)]lnf = array(lnf)for i in range(0, rows):for j in range(0, cols):if x[i][j] == 0:lnfij = 0.0else:p = x[i][j] / np.sum(x, axis=0)[j]lnfij = math.log(p) * p * (-k)lnf[i][j] = lnfijlnf = pd.DataFrame(lnf)E = lnf# 计算一致性程度d = 1 - E.sum(axis=0)# 计算各指标的权重w = [[None] * 1 for i in range(cols)]for j in range(0, cols):wj = d[j] / sum(d)w[j] = wjw = pd.DataFrame(w)w.index = df.columnsw.columns = ['权重']return w

三、xgb指标评价

介绍

1. xgboost 的全称是eXtreme Gradient Boosting，由华盛顿大学的陈天奇博士提出，在Kaggle的希格斯子信号识别竞赛中使用，因其出众的效率与较高的预测准确度而引起了广泛的关注。

2. 与GBDT的区别
   GBDT算法只利用了一阶的导数信息，xgboost对损失函数做了二阶的泰勒展开，并在目标函数之外加入了正则项对整体求最优解，用以权衡目标函数的下降和模型的复杂程度，避免过拟合。所以不考虑细节方面，两者最大的不同就是目标函数的定义，接下来就着重从xgboost的目标函数定义上来进行介绍。

3. xgboost的模型
   xgboost对应的模型就是一堆CART树。一堆树如何做预测呢？就是将每棵树的预测值加到一起作为最终的预测值，可谓简单粗暴。

XGBoost的基本思想

在XGBoost里，每棵树是一个一个往里面加的，每加一个都是希望效果能够提升，下图就是XGBoost这个集成的表示（核心）。
一开始树是0，然后往里面加树，相当于多了一个函数，再加第二棵树，相当于又多了一个函数…等等，这里需要保证加入新的函数能够提升整体对表达效果。提升表达效果的意思就是说加上新的树之后，目标函数（就是损失）的值会下降。

如果叶子结点的个数太多，那么过拟合的风险会越大，所以这里要限制叶子结点的个数，所以在原来目标函数里要加上一个惩罚项「omega(ft)」。

XGBoost算法完整的目标函数

求目标函数的过程：
给目标函数对权重求偏导，得到一个能够使目标函数最小的权重，把这个权重代回到目标函数中，这个回代结果就是求解后的最小目标函数值，如下：

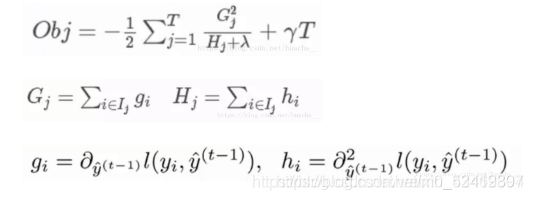
其中第三个式子中的一阶导二阶导的梯度数据都是可以算出来的，只要指定了主函数中的两个参数，这就是一个确定的值。下面给出一个直观的例子来看下这个过程。

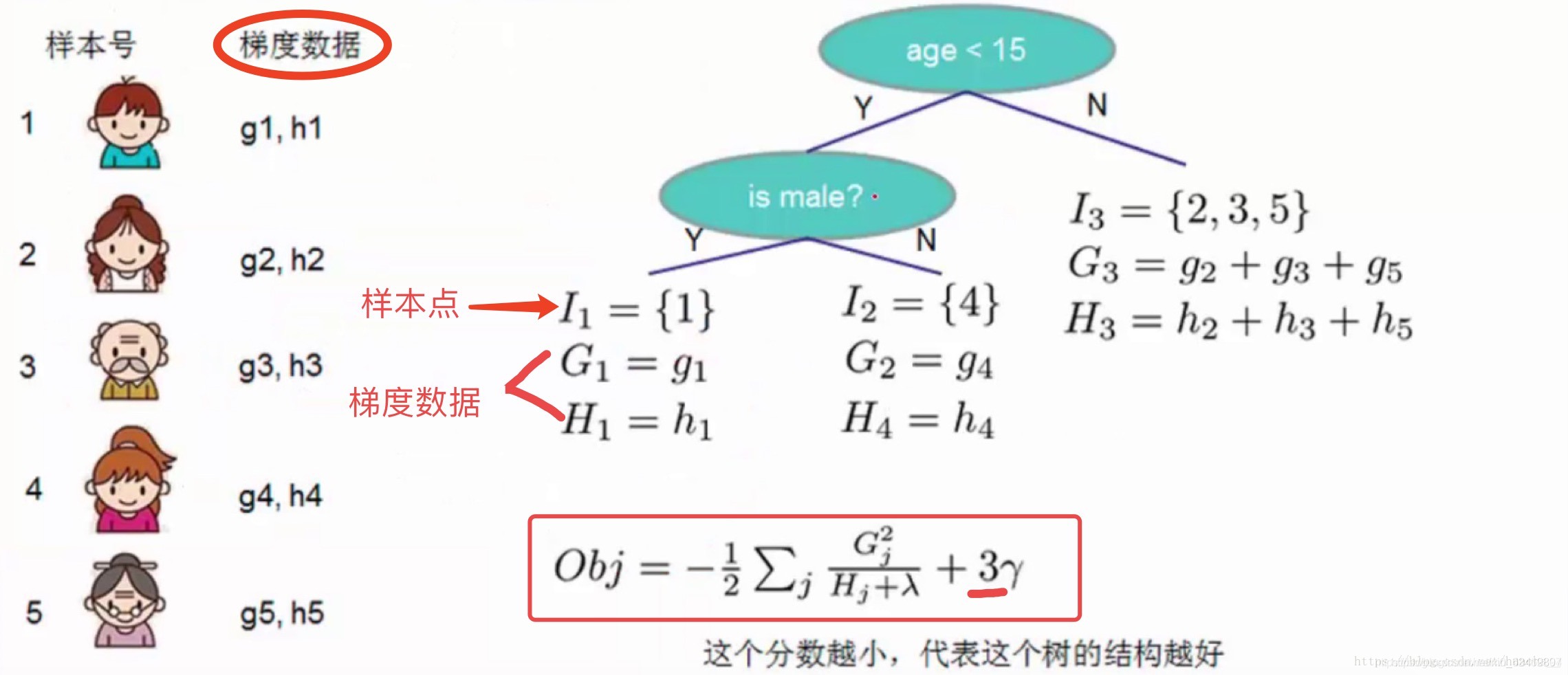
1. Obj代表了当我们指定一个树的结构的时候，在目标上最多会减少多少，我们可以把它叫做结构分数，这个分数越小越好

对于每次扩展，我们依旧要枚举所有可能的方案。对于某个特定的分割，我们要计算出这个分割的左子树的导数和和右子数导数和之和（就是下图中的第一个红色方框），然后和划分前的进行比较（基于损失，看分割后的损失和分割前的损失有没有发生变化，变化了多少）。遍历所有分割，选择变化最大的作为最合适的分割。

用python实现XGBoost算法

import xgboost
from numpy import loadtxt
from xgboost import XGBClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 载入数据集
dataset = loadtxt('pima-indians-diabetes.csv', delimiter=",")
# split data into X and y
X = dataset[:,0:8]
Y = dataset[:,8]# 把数据集拆分成训练集和测试集
seed = 7
test_size = 0.33
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=test_size, random_state=seed)# 拟合XGBoost模型
model = XGBClassifier()
model.fit(X_train, y_train)# 对测试集做预测
y_pred = model.predict(X_test)
predictions = [round(value) for value in y_pred]# 评估预测结果
accuracy = accuracy_score(y_test, predictions)
print("Accuracy: %.2f%%" % (accuracy * 100.0))

XGBoost的优化

1. 在寻找最佳分割点时，考虑传统的枚举每个特征的所有可能分割点的贪心法效率太低，xgboost实现了一种近似的算法。大致的思想是根据百分位法列举几个可能成为分割点的候选者，然后从候选者中根据上面求分割点的公式计算找出最佳的分割点。
2. xgboost考虑了训练数据为稀疏值的情况，可以为缺失值或者指定的值指定分支的默认方向，这能大大提升算法的效率，paper提到50倍.
3. 特征列排序后以块的形式存储在内存中，在迭代中可以重复使用；虽然boosting算法迭代必须串行，但是在处理每个特征列时可以做到并行。
4. 按照特征列方式存储能优化寻找最佳的分割点，但是当以行计算梯度数据时会导致内存的不连续访问，严重时会导致cache miss，降低算法效率。paper中提到，可先将数据收集到线程内部的buffer,然后再计算，提高算法的效率。
5. xgboost还考虑了当数据量比较大，内存不够时怎么有效的使用磁盘，主要是结合多线程、数据压缩、分片的方法，尽可能的提高算法的效率。

xgboost的优势：

1、正则化
标准GBM的实现没有像XGBoost这样的正则化步骤。正则化对减少过拟合也是有帮助的。
实际上，XGBoost以“正则化提升(regularized boosting)”技术而闻名。

2、并行处理
XGBoost可以实现并行处理，相比GBM有了速度的飞跃，LightGBM也是微软最新推出的一个速度提升的算法。 XGBoost也支持Hadoop实现。

3、高度的灵活性
XGBoost 允许用户定义自定义优化目标和评价标准 。

4、缺失值处理
XGBoost内置处理缺失值的规则。用户需要提供一个和其它样本不同的值，然后把它作为一个参数传进去，以此来作为缺失值的取值。XGBoost在不同节点遇到缺失值时采用不同的处理方法，并且会学习未来遇到缺失值时的处理方法。

5、剪枝
当分裂时遇到一个负损失时，GBM会停止分裂。因此GBM实际上是一个贪心算法。XGBoost会一直分裂到指定的最大深度(max_depth)，然后回过头来剪枝。如果某个节点之后不再有正值，它会去除这个分裂。
这种做法的优点，当一个负损失（如-2）后面有个正损失（如+10）的时候，就显现出来了。GBM会在-2处停下来，因为它遇到了一个负值。但是XGBoost会继续分裂，然后发现这两个分裂综合起来会得到+8，因此会保留这两个分裂。

6、内置交叉验证
XGBoost允许在每一轮boosting迭代中使用交叉验证。因此，可以方便地获得最优boosting迭代次数。
而GBM使用网格搜索，只能检测有限个值。

7、在已有的模型基础上继续
XGBoost可以在上一轮的结果上继续训练。
sklearn中的GBM的实现也有这个功能，两种算法在这一点上是一致的。

*ps:*本文参考的资料：

1. XGBoost——机器学习https://blog.csdn.net/weixin_42462804/article/details/104352985?utm_source=app&app_version=4.5.5
2. 熵权法（客观赋权法)https://blog.csdn.net/weixin_43819566/article/details/112396912
3. 用Python的sklearn库进行PCA https://blog.csdn.net/puredreammer/article/details/52255025

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！