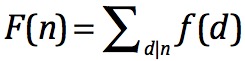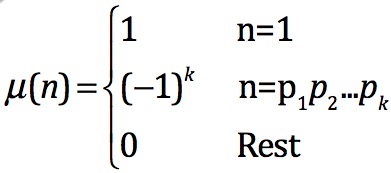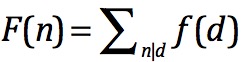莫比乌斯函数求法
一、单独求解
#include using namespace std;
typedef long long ll;
//计算a是否可以mod b
int MOD(int a,int b)
{return a-a/b*b;
}//计算莫比乌斯函数
//如果一个数包含平方因子,那么miu(n)=0
//如果哟个数不包含平方因子,且有k个不同的质因子,那么miu(n)=(-1)^kint miu(int n)
{int cnt,k=0;for(int i=2;i*i=2){return 0;}}if(n!=1){k++;}return MOD(k,2)?-1:1;
}int main()
{//cout << "Hello world!" << endl;ll n;cin>>n;cout<
二、线性筛法求解
/** 莫比乌斯反演公式* 线性筛法求解积性函数(莫比乌斯函数)*/
const int MAXN = 1000000;
bool check[MAXN + 10];
int prime[MAXN + 10];
int mu[MAXN + 10];void Moblus()
{memset(check, false, sizeof(check));mu[1] = 1;int tot = 0;for (int i = 2; i <= MAXN; i++){if (!check[i]){prime[tot++] = i;mu[i] = -1;}for (int j = 0; j < tot; j++){if (i * prime[j] > MAXN){break;}check[i * prime[j]] = true;if (i % prime[j] == 0){mu[i * prime[j]] = 0;break;}else{mu[i * prime[j]] = -mu[i];}}}
}本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!