斐波那契数列的暴力递归方法使用动态规划进行优化
斐波那契数列指的是这样一个数列:1、1、2、3、5、8、13、21、34…
即从第二位开始,每一位都符合一个特征:f(n) = f(n-2) + f(n-1)。
1. 暴力递归解法
/*** 时间复杂度为:O(2^n)* @param n 第几位数* @return 返回第n位上的斐波那契数*/public static long fibonacci(int n){if(n < 1){return 0;}return process(n);}public static long process(int n){if(n==1 || n==0){return 1;}return process(n-1) + process(n-2);}
为了分析其时间复杂度,我们不妨假设n=4,分析图:
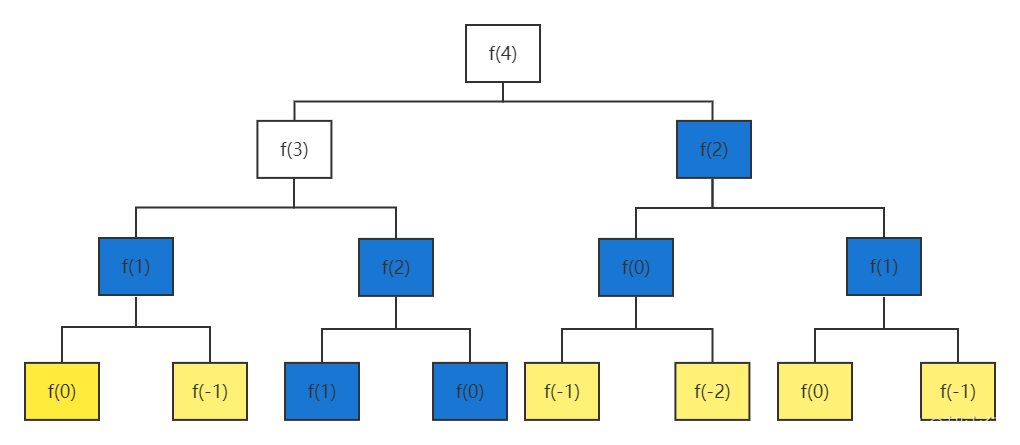
单论这个例子,可以发现,当n=4时候,一个会创建出15个方法,也就是2^4 - 1。但是由于n=1或n=0时可以直接返回,所以实际创建方法需要减去黄色板块的方法,而实际调用方法数为:2^4 - 7,而忽略其常数项,实际时间复杂度为O(2^4) 即 O(2^n),2的n次方。
在分析图中,有许多重复调用的方法,即蓝色板块,如:f(1)反复调用了3次,f(2)反复调用了2次,f(0)反复调用了2次。利用缓存的思想我们可以进行第一步优化。
2. 记忆化搜索
/*** 时间复杂度为:O(n * buffer.length)* @param n 第几位数* @return 返回第n位上的斐波那契数*/public static long fibonacciUsingBuffer(int n){if(n < 1){return 0;}long [] buffer = new long[n + 1];for (int i = 0; i < buffer.length; i++) {buffer[i] = -1;}return process2(n,buffer);}public static long process2(int n,long[] buffer){if(buffer[n] != -1){return buffer[n];}if(n==1||n==0){buffer[n] = 1;return buffer[n];}buffer[n] = process2(n-1,buffer) + process2(n-2,buffer);return buffer[n];}
这种优化利用了了一个buffer缓存(可以为数组,也可以为Map集合),长度为n+1,因为需要存第n位的值,初始化值为-1,当调用递归方法时,优先判断缓存中是否有该位置对应的值,如果有则直接返回,无需再进行递归了。
利用记忆化搜索的优化方案,由于buffer数组中的值每一个都会被赋值,所以它的时间复杂度为:O(n * buffer.length)。
但是,在斐波那契这个数列例子中,我们可以发现buffe的长度为n+1!遍历的范围为0~n,所以我们可以得出O(n * buffer.length) 其实趋向于O(n*n),即O(n²)。但怎么也要比第一种O(2^n)次方好的多,可以假设n=50带入计算,之间的差距是相当大的。
3. 精细化动态规划
/*** 时间复杂度为:O(N)* @param n 第几位数* @return 返回第n位上的斐波那契数*/public static long fibonacciDpWay(int n){if(n<1){return 0;}long[] arr = new long[n + 1];arr[1] = 1;arr[0] = 1;for (int i = 2; i < arr.length; i++) {arr[i] = arr[i-1] + arr[i-2];}return arr[n];}
该方法直接把时间复杂度干到了O(N)。使用了一个数组,数组的长度即为需要求的斐波那契数列相应的位数,将第0个和第1个位置设置为1,开始遍历该数组,只需遍历一次!便可得到最终答案,返回arr[N]即可!
精细化动态规划,把n作为可变参数且代表状态,只需得出n相应的值便获得了该算法的解。

4. 总结
当n=50时,求相应的斐波那契数,三种算法的效率对比如下所示:
| 暴力递归 | 记忆化搜索 | 精细化动态规划 | |
|---|---|---|---|
| 50 | 50690ms | 0ms | 0ms |
明显可以发现记忆化搜索和精细动态规划效率高的多的多的多的多:) 暴力递归跑了50秒将近一分钟。
再使n=500,这次只比较记忆搜索法和精细化动态规划的效率
| 记忆化搜索 | 精细化动态规划 | |
|---|---|---|
| 500 | 5ms | 0ms |
最终效率对比的结果和我们时间复杂度分析出来的结果一直,精细化动态规划使其时间复杂度为O(N),为当前三种方法的最优解。
在不同场景下,精细化动态规划的结果也不一定比记忆化搜索好。精细化动态规划把可变参数做最细致的划分,但划分的状态有可能有很多是实际暴力递归种用不到的状态(在斐波那契数列中,划分的状态在暴力递归都使用到了),即n=50时,在精细化动态规划种需要求出1~50的值,若这些结果值在暴力递归中都使用到了或者使用了大部分(在斐波那契数列中,求第50个位置的值是需要求出1 ~ 49位置上的值),那么精细化动态规划的结果是要比记忆化搜索要好的,若这些结果只要使用几个,那么此时记忆化搜索,缓存结果值更优。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!