拉普拉斯矩阵相关

拉普拉斯矩阵相关

拉普拉斯矩阵

Laplacian matrix的定义

拉普拉斯矩阵（Laplacian matrix)），也称为基尔霍夫矩阵, 是表示图的一种矩阵。给定一个有n个顶点的图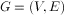，其拉普拉斯矩阵被定义为:

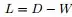
其中为图的度矩阵，为图的邻接矩阵。

举个例子。给定一个简单的图，如下：

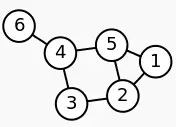
把此“图”转换为邻接矩阵的形式，记为：

把的每一列元素加起来得到个数，然后把它们放在对角线上（其它地方都是零），组成一个的对角矩阵，记为度矩阵，如下图所示：

根据拉普拉斯矩阵的定义，可得拉普拉斯矩阵 为：

1.2、 拉普拉斯矩阵的性质
介绍 拉普拉斯矩阵的性质之前，首先定义两个概念，如下：

①对于邻接矩阵，定义图中A子图与B子图之间所有边的权值之和如下：

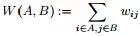
其中wij ，定义为节点到节点的权值，如果两个节点不是相连的，权值为零。
②与某结点邻接的所有边的权值和定义为该顶点的度d，多个d 形成一个度矩阵 （对角阵）

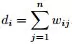
拉普拉斯矩阵 具有如下性质：

L是对称半正定矩阵；

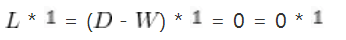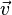，即 L的最小特征值是0，相应的特征向量是 。证明： 。（此外，别忘了，之前特征值和特征向量的定义：若数字和非零向量满足，则为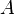的一个特征向量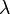，是其对应的特征值）。

L 有n个非负实特征值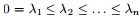

且对于任何一个属于实向量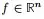，有以下式子成立

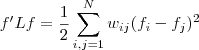
其中，

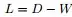
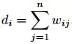
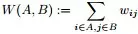
下面，来证明下上述结论，如下：

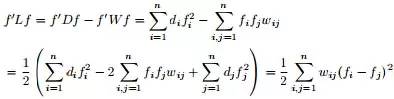
来源来源

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！