最长下降子序列
文章目录
- 题目
- 解法
- DP+暴搜
- 思路
- 代码实现
- 贪心+二分
- 思路
- 代码实现
题目
给出一组数据 nums,求出其最长下降子序列(子序列允许不连续)的长度。(类似于lc的最长递增子序列)
示例:
输入:
6 // 数组元素个数
3 4 3 5 2 1 // 数组
输出:
4 // 最长下降子序列为4321,长度为4
解法
DP+暴搜
思路
DP数组 表示 nums数组 对应下标的元素作为末尾时最长下降子序列的长度,因此将 DP数组中的元素 全部初始化为 1(最起码这个下降子序列里有当前元素)。
从 nums 的第二个元素开始(记为 i),向前搜索所有大于它的元素(记为 j),找到后 dp[i] = max(dp[i], dp[j] + 1) 。举个例子会更直观:
nums = 3 4 3 5 2 1
dp = 1 1 2 1 3 4⬆形成下降子序列:4,3
在 i=4, nums[i]=2 时,这个状态转移方程显得尤为重要:
- 从
j=0开始遍历,第一个大于2的元素是j=1, nums[j]=4,dp[i]=dp[j]+1=2,意味着可以形成下降子序列:4,2,长度为dp[i]=2; - 第二个大于
2的元素是j=2, nums[j]=3,dp[i]=dp[j]+1=3,意味着可以形成下降子序列:4,3,2 - 第三个大于
2的元素是j=3, nums[j]=5,dp[i]=dp[i]=3,意味着形成5,2不如形成4,3,2更长,所以仍保持原来的下降子序列。
值得注意的是最长下降子序列的长度是 DP数组 中最大的元素而非尾元素,举个例子:
nums = 3 4 3 5 2 3
dp = 1 1 2 1 3 2
因此在构建 DP数组 的同时要记得保存最大元素哦~
代码实现
int main() {int n, res = 1;cin >> n;vector<int> v(n), dp(n, 1);for (int i = 0; i < n; i++) {cin >> v[i];}for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (v[j] > v[i]) dp[i] = max(dp[j] + 1, dp[i]);}res = max(dp[i], res);}cout << res << endl;
}

贪心+二分
思路
dp数组: 用来暂存一个 下降子序列,注意,这里的序列并非真正的最长下降子序列,至于原因下文解释。由于题目要求的是最长下降子序列的长度,并不用返回序列的具体排列,因此dp数组的长度就是本题的答案。
该方法思路分三步:请客、斩首、收下当狗。
- 请客:遍历
数据数组中每个元素,和dp数组的尾元素比较。 - 收下当狗:如果比较结果是当前遍历到的元素小于
dp数组尾元素,则当前元素直接加入dp数组,成为新的尾元素。 - 斩首:斩
dp数组中旧元素的首,当前遍历到的元素作为新元素,自然要先收下当狗,具体做法是:- 通过二分法找到
dp数组中所有小于当前元素中最大的那个,用当前元素替换掉它。举个例子,比如:dp数组元素是9,5,3,1。当前遍历到的元素是6,那么dp数组会变成:9,6,3,1。
- 通过二分法找到
为什么说
dp数组暂存的下降子序列只是和真正的最长下降子序列长度相等,两者内容并不一样?
原因就在于第3点——斩首,斩首的目的是 在不改变子序列长度的基础上扩大下降子序列的最小值,用具体例子来说明:
假如给出的数据是 3,4,3,5,2,1。那么 dp数组 的变化会是:
| dp数组内容 | 当前遍历到的元素 | 最长下降子序列 | |
|---|---|---|
| 3 | 3 | 3 |
| 4 | 4 | 4 或 3 |
| 4,3 | 3 | 4,3 |
| 5,3 | 5 | 4,3 |
| 5,3,2 | 2 | 4,3,2 |
| 5,3,2,1 | 1 | 4,3,2,1 |
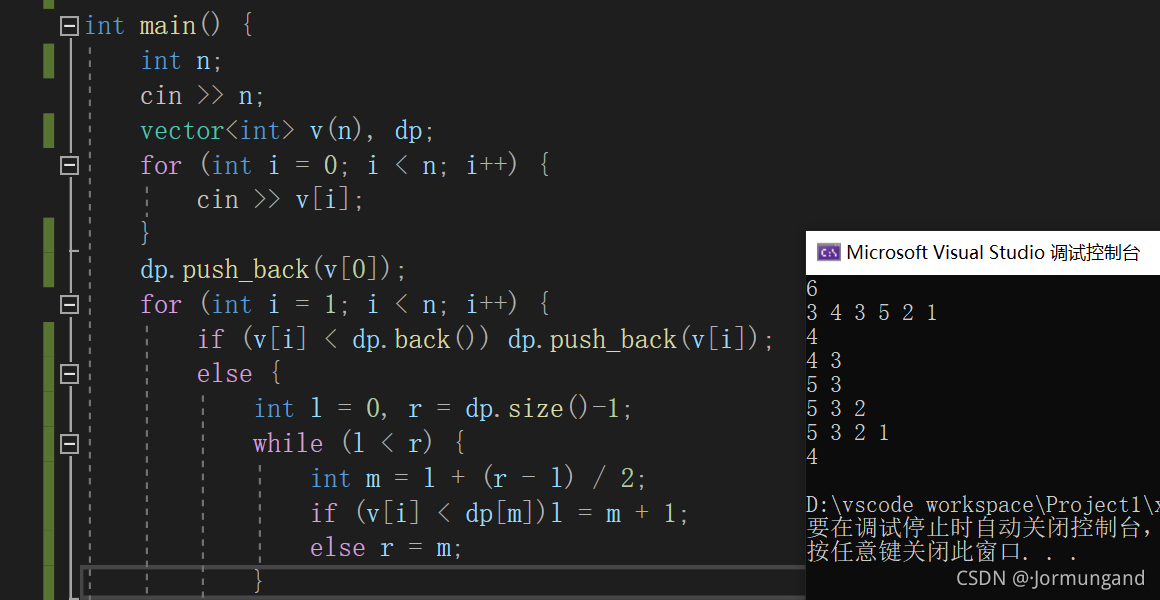
代码实现
int main() {int n;cin >> n;vector<int> v(n), dp;for (int i = 0; i < n; i++) {cin >> v[i];}dp.push_back(v[0]);for (int i = 1; i < n; i++) {if (v[i] < dp.back()) dp.push_back(v[i]);else {int l = 0, r = dp.size()-1;while (l < r) {int m = l + (r - l) / 2;if (v[i] < dp[m])l = m + 1;else r = m;}dp[l] = v[i];}for (int j : dp) {cout << j << " ";}cout << endl;}cout << dp.size() << endl;
}
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!