求两数的最大公约数和最小公倍数三种方法（定义，辗转相除法与实用方法）

从定义入手：

首先，从定义上我们理解两个数（以下简称a,b)的公倍数都能刚好整除a和b,也就是余数为0.考虑到最小公倍数可能在两个数之中（如20，10），我们仅需从a和b的较大值开始循环加1就能确保找到最小的公倍数，并通过公式a*b=最大公约数*最小公倍数算出最大公约数。

辗转相除法

第二种方法是利用了递归技巧的辗转相除法，通过a与b相除并建立函数不断地将除数赋值给被除数，将余数赋值给被除数的方法，当余数等于0时，这个式子的除数就是a与b的最大公约数。不用担心较小数除较大数，在下一次进入函数时会将两者位置互换。

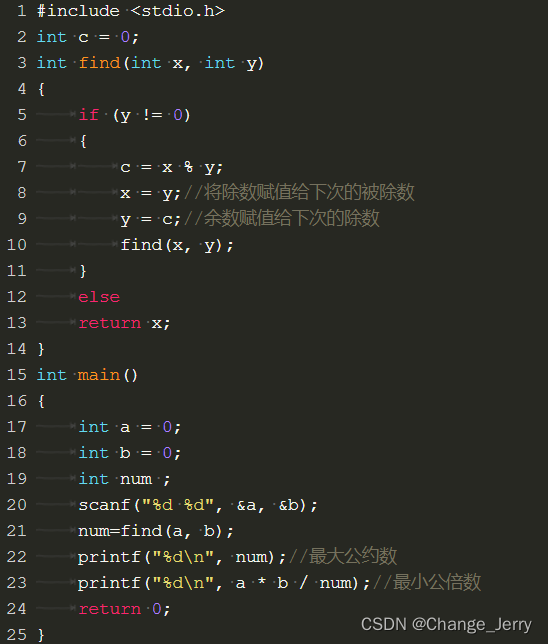
实用方法：

递归虽然简洁易懂，但会一直重复的计算，甚至于做无用功，效率方面往往不尽人意。那接下来要就需要找到一种高效的方法了。我们不妨假设我们已经知道了最小公倍数，那么这个数除a一定等于一个整数i,我们就能够用(a*i)表示最小公倍数，我们仅需找到i的值。而已知最小公倍数除b的余数为0，将这作为循环的停止条件，便能找出i的值了。注意，这里i需要从1开始递增。如下

#include
int main()
{
    int a = 0;
    int b = 0;
    scanf("%d %d", &a, &b);
    int i = 1;
    while (a * i % b != 0)
    {
        i++;
    }
    printf("%d\n", a * i);
    printf("%d\n", b / i);
    return 0;
}

本篇忽略了输入值为0、栈溢出等特殊情况，希望能对你有帮助。有错误或不妥的地方，还望指出并提供宝贵意见。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！